Storyboard

Die Durchschnittsgeschwindigkeit wird definiert, indem die zurückgelegte Strecke über einen vergangenen Zeitraum betrachtet wird, ohne mögliche Geschwindigkeitsschwankungen zu berücksichtigen.

Um die Geschwindigkeit zu einem bestimmten Zeitpunkt zu bestimmen, ist es notwendig, ein unendlich kleines Zeitintervall zu betrachten, so dass die Geschwindigkeit innerhalb dieses Intervalls nahezu konstant bleibt.

Dies führt zur Berechnung der momentanen Geschwindigkeit, indem die Durchschnittsgeschwindigkeit im Grenzwert für ein Zeitintervall berechnet wird, das gegen Null strebt. Mathematisch entspricht dies der Ableitung der Position nach der Zeit und stellt die Steigung der Position-Zeit-Kurve dar.

>Modell

ID:(1432, 0)

Definition

Auf der einen Seite ist es wichtig, zwischen dem einfachsten Fall, der eindimensional ist, und dem komplexeren Fall mit mehr als einer Dimension zu unterscheiden. In beiden Fällen entspricht die Ableitung von die Position ($s$) nach der Zeit ($t$), was der Steigung der Kurve von die Position ($s$) entspricht, die Geschwindigkeit ($v$). Ebenso entspricht die Ableitung von die Posición (Vektor) ($\vec{s}$) nach der Zeit ($t$) Die Geschwindigkeit (Vektor) ($\vec{v}$).

Auf der anderen Seite ermöglicht uns die Fläche unter der Kurve von die Geschwindigkeit ($v$) bei der Zeit ($t$), was der Integration entspricht, die Berechnung von die Position ($s$).

ID:(15393, 0)

Bild

Die Geschwindigkeit ($v$) wird als die Verlagerung pro Zeiteinheit definiert. Dieses Konzept reduziert sich jedoch auf eine Mittlere Geschwindigkeit ($\bar{v}$), das während des betrachteten Zeitintervalls existiert.

Die Begrenztheit der Durchschnittsgeschwindigkeit zeigt sich darin, dass angenommen wird, dass ein Objekt sofort von Ruhe in eine gegebene Geschwindigkeit übergeht. Es ist, als würde ein Bus sofort nach dem Verlassen seines Terminals eine Reisegeschwindigkeit erreichen, was völlig absurd ist. Die Geschwindigkeit entwickelt sich, nimmt zu, nimmt ab (Ampel, Fahrgäste steigen ein) und steigt langsam an, bis sie einen mehr oder weniger konstanten Wert erreicht, wenn sie auf der Straße fährt. Auf diese Weise wird ein Bus, der normalerweise mit etwa 100 km/h auf der Straße fährt, mehr als 8 Stunden brauchen, um 800 km zurückzulegen, da die Geschwindigkeitsfluktuationen berücksichtigt werden müssen. Am Ende wird er 10 Stunden für 800 km gebraucht haben und mit einer Durchschnittsgeschwindigkeit von 80 km/h gefahren sein.

Wenn man die Geschwindigkeit zu jedem Zeitpunkt kennen möchte, muss man eine so kleine Zeit wählen, dass während dieser Zeit die Geschwindigkeit annähernd konstant sein kann. Dadurch entspricht die auf diese Weise geschätzte Durchschnittsgeschwindigkeit der Geschwindigkeit, die zum betreffenden Zeitpunkt existiert.

Deshalb sprechen wir von der momentanen Geschwindigkeit.

ID:(16, 0)

Notiz

Wenn wir ein Zeit ($t$) mit eine Position ($s$) ($s(t)$) nehmen und einen Punkt zu einer zukünftigen Zeit $t+\Delta t$ mit einer Position $s(t+\Delta t)$ betrachten, können wir die Geschwindigkeit als die Strecke im Zeitintervall $\Delta t$ abschätzen:

$s(t+\Delta t)-s(t)$

die Geschwindigkeit ($v$) kann berechnet werden, indem man die zurückgelegte Strecke durch die vergangene Zeit teilt:

$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$

Wenn der Wert von $\Delta t$ kleiner wird, nähert sich die berechnete Geschwindigkeit der Tangente an die Positionscurve zur Zeit:

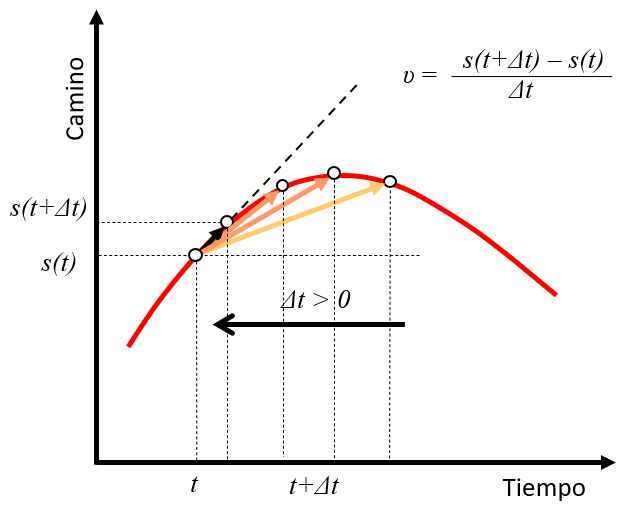
Dies verallgemeinert das, was bereits für den Fall konstanter Geschwindigkeit gesehen wurde.

ID:(1638, 0)

Zitat

Das Integral von die Geschwindigkeit ($v$) entspricht dem Bereich unter der Kurve, die diese Funktion definiert. Daher entspricht das Integral der Geschwindigkeit zwischen der Startzeit ($t_0$) und der Zeit ($t$) der zurückgelegten Strecke zwischen die Ausgangsstellung ($s_0$) und die Position ($s$).

Deshalb haben wir:



Was in der folgenden Grafik dargestellt ist:

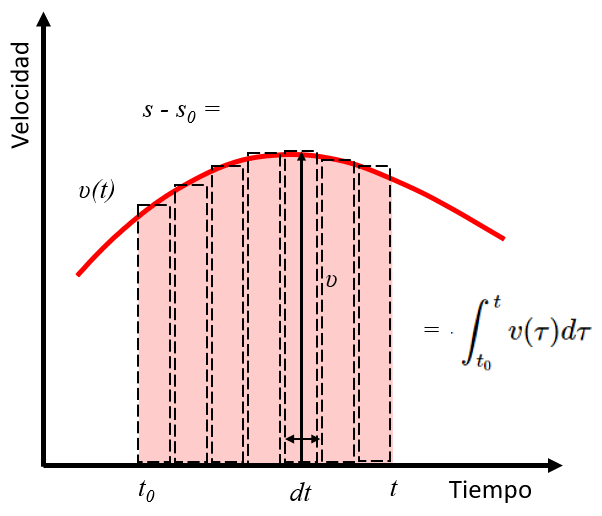
Ich gehe als Bereich unter der Geschwindigkeits- und Zeitkurve.

ID:(2242, 0)

Übung

Für Bewegungen, die in mehr als einer Dimension stattfinden, muss die Beschreibung der Bewegung in einer Dimension verallgemeinert werden. Dies wird erreicht, indem mit einer Version mit mehreren Dimensionen für die Position gearbeitet wird. Im Falle von drei Dimensionen sieht dies wie folgt aus:

$s \rightarrow \vec{s} = (x, y, z)$

Analog dazu kann die Ableitung des Vektors nach der Zeit definiert werden, was den Geschwindigkeitsvektor ergibt:

$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$

Dies lässt sich in der folgenden grafischen Darstellung zusammenfassen:

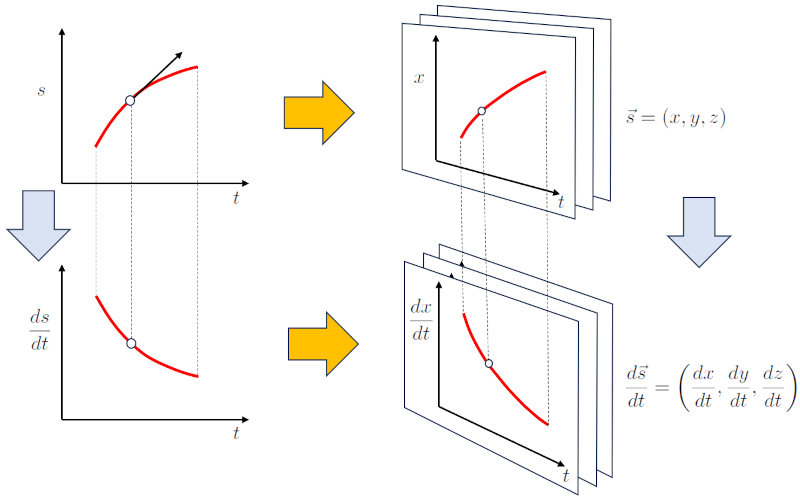
ID:(15506, 0)

Gleichung

Im Fall einer Dimension steht die Geschwindigkeit ($v$) in Beziehung zu die Position ($s$) durch ihre Ableitung bei der Zeit ($t$), während das Integral von die Geschwindigkeit ($v$) über das Intervall von der Zeit ($t$) bis der Startzeit ($t_0$) Die Position ($s$) ab die Ausgangsstellung ($s_0$) ergibt. In einem allgemeineren Kontext, in mehr als einer Dimension, kann die Funktion die Posición (Vektor) ($\vec{s}$) bei der Zeit ($t$) abgeleitet werden, was zu die Geschwindigkeit (Vektor) ($\vec{v}$) führt.

ID:(15391, 0)