Mit konstanter Geschwindigkeit abfangen
Storyboard 
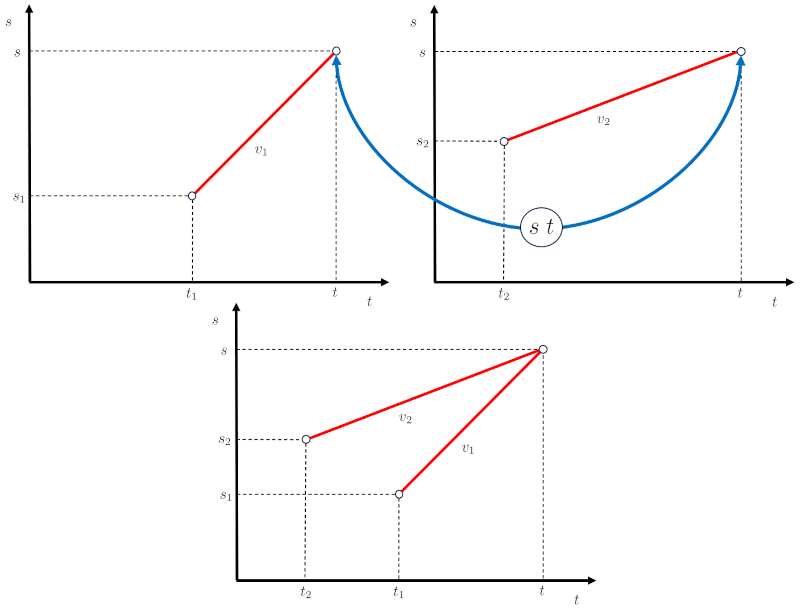
Objekte können sich kreuzen, wenn sie zum selben Zeitpunkt am selben Ort zusammenfallen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Startpunkten aus mit Geschwindigkeiten bewegen, die es ihnen ermöglichen, am Ende der Reise am selben Ort und zur gleichen Zeit zu sein.
ID:(445, 0)
Mit konstanter Geschwindigkeit abfangen
Storyboard 
Objekte können sich kreuzen, wenn sie zum selben Zeitpunkt am selben Ort zusammenfallen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Startpunkten aus mit Geschwindigkeiten bewegen, die es ihnen ermöglichen, am Ende der Reise am selben Ort und zur gleichen Zeit zu sein.
Variablen
Berechnungen
Berechnungen
Gleichungen
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
Die Gleichung f r die durchschnittliche Geschwindigkeit:
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
Die Gleichung f r die durchschnittliche Geschwindigkeit:
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
Beispiele
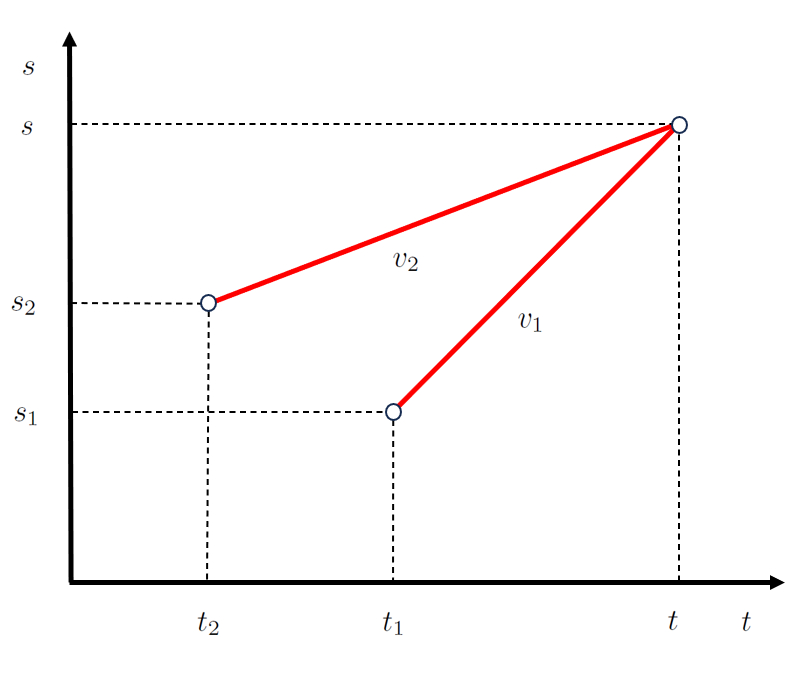
W hrend des Intersektionsprozesses bewegen sich zwei K rper so, dass sie bei die Kreuzungsposition ($s$) und der Kreuzungszeit ($t$) bereinstimmen.
Daf r muss jeder K rper von seiner Ausgangsposition und -zeit aus starten, mit Verschiebungen von jeweils die Geschwindigkeit der ersten Stufe ($v_1$) und die Geschwindigkeit der ersten Stufe ($v_1$), so dass die bereinstimmung eintritt.
Im Fall einer Interzeption handelt es sich um zwei K rper, die sich so bewegen, dass sie sich bei ein Kreuzungszeit ($t$) in ihrer ERROR:10258,0 treffen werden.
Zu diesem Zweck:
• Beginnt jeder K rper seine Bewegung bei der Anfangszeit des ersten Objekts ($t_1$), wobei die Anfangsposition des ersten Objekts ($s_1$) seine Ausgangsposition und die Geschwindigkeit der ersten Stufe ($v_1$) seine Verschiebung ist.
• Beginnt jeder K rper seine Bewegung bei der Anfangszeit des zweiten Objekts ($t_2$), wobei die Anfangsposition des zweiten Objekts ($s_2$) seine Ausgangsposition und die Geschwindigkeit der zweiten Stufe ($v_2$) seine Verschiebung ist.
Diese Bedingungen m ssen erf llt sein, damit es zur Interzeption kommt.
Damit k nnen die Diagramme der Position im Laufe der Zeit wie folgt gekoppelt werden:
Im Falle einer Kreuzung oder Kollision zwischen zwei Objekten ist es blich, dass die Geschwindigkeit der ersten Stufe ($v_1$) und die Geschwindigkeit der zweiten Stufe ($v_2$) so sein m ssen, dass eine bereinstimmung erfolgt.
Das bedeutet, dass die Vom ersten Objekt zurückgelegte Entfernung ($\Delta s_1$) und die Reisezeit des ersten Objekts ($\Delta t_1$) zu eine Geschwindigkeit der ersten Stufe ($v_1$) f hren m ssen,
so dass mit die Vom zweiten Objekt zurückgelegte Entfernung ($\Delta s_2$) und die Reisezeit des zweiten Objekts ($\Delta t_2$) Eine Geschwindigkeit der zweiten Stufe ($v_2$) erreicht wird,
damit sie letztendlich in Zeit und Raum (Position) bereinstimmen:
Im Fall einer Bewegung, bei der sich zwei Objekte schneiden, wie zum Beispiel die Kreuzungsposition ($s$) und der Kreuzungszeit ($t$), ist dies f r beide blich. Daher, wenn f r das erste Objekt der Anfangszeit des ersten Objekts ($t_1$) und die Anfangsposition des ersten Objekts ($s_1$) mit die Geschwindigkeit der ersten Stufe ($v_1$) erf llt sind:
und f r das zweite Objekt der Anfangszeit des zweiten Objekts ($t_2$) und die Anfangsposition des zweiten Objekts ($s_2$) mit die Geschwindigkeit der zweiten Stufe ($v_2$) erf llt sind:
was wie folgt dargestellt wird:
Der Schl ssel liegt darin, dass sich beide Objekte bei die Kreuzungsposition ($s$) zur Zeit der Kreuzungszeit ($t$) treffen. Daf r startet Objekt 1 seine Reise bei die Anfangsposition des ersten Objekts ($s_1$) zu ein Anfangszeit des ersten Objekts ($t_1$) mit einer Geschwindigkeit von eine Geschwindigkeit der ersten Stufe ($v_1$), w hrend Objekt 2 seine Reise bei die Anfangsposition des zweiten Objekts ($s_2$) zu ein Anfangszeit des zweiten Objekts ($t_2$) mit einer Geschwindigkeit von eine Geschwindigkeit der zweiten Stufe ($v_2$) beginnt. W hrend dieses Prozesses bewegt sich Objekt 1 Eine Vom ersten Objekt zurückgelegte Entfernung ($\Delta s_1$) bei eine Reisezeit des ersten Objekts ($\Delta t_1$), w hrend Objekt 2 Eine Vom zweiten Objekt zurückgelegte Entfernung ($\Delta s_2$) bei eine Reisezeit des zweiten Objekts ($\Delta t_2$) zur cklegt:
Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
ID:(445, 0)