Storyboard

The average velocity is defined by considering the distance traveled over an elapsed time interval, without accounting for potential velocity fluctuations.

To determine velocity at a specific instant, it is necessary to consider an infinitesimally small time interval so that the velocity remains nearly constant within that interval.

This leads to the calculation of instantaneous velocity by computing the average velocity in the limit as the time interval approaches zero. Mathematically, this corresponds to the derivative of position with respect to time and represents the slope of the position-time curve.

>Model

ID:(1432, 0)

Definition

On one hand, it's important to differentiate between the simplest case, which is one-dimensional, and the more complex case involving more than one dimension. In both cases, the derivative of the position ($s$) with respect to the time ($t$), which corresponds to the slope of the curve of the position ($s$), is equal to the speed ($v$). Similarly, the derivative of the posición (vector) ($\vec{s}$) with respect to the time ($t$), corresponds to the speed (Vector) ($\vec{v}$).

On the other hand, the area under the curve of the speed ($v$) at the time ($t$), which corresponds to integration, allows us to calculate the position ($s$).

ID:(15393, 0)

Image

The speed ($v$) is defined as the displacement per unit of time. However, this concept is reduced to ERROR:5268.1 that exists during the interval of time considered.

The limitation of the average velocity is reflected in the assumption that an object instantly goes from rest to a given velocity. It is as if a bus that has just left the terminal suddenly reaches cruising speed, which is totally absurd. The velocity evolves, increases, decreases (due to a traffic light or picking up passengers), and slowly increases until it reaches a more or less constant value when traveling on the road. Therefore, a bus that normally travels on the road at around 100 km/h will take more than 8 hours to cover 800 km because the fluctuations in velocity must be taken into account. In the end, it will have taken 10 hours to cover 800 km traveling at an average speed of 80 km/h.

If we want to know the velocity at each moment, we must take a time interval so small that during this time, the velocity can be considered approximately constant. Thus, the average velocity estimated in this way is equivalent to the velocity that exists at the considered moment.

That's why we talk about instantaneous velocity.

ID:(16, 0)

Note

If we take ERROR:5264.1 with ERROR:9899.1 ($s(t)$) and observe a point at a future time $t+\Delta t$ with a position $s(t+\Delta t)$, we can estimate the velocity as the distance traveled in the time $\Delta t$:

$s(t+\Delta t)-s(t)$

the speed ($v$) can be calculated by dividing the distance traveled by the elapsed time:

$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$

As the value of $\Delta t$ becomes smaller, the calculated velocity approaches the tangent to the position curve at the time:

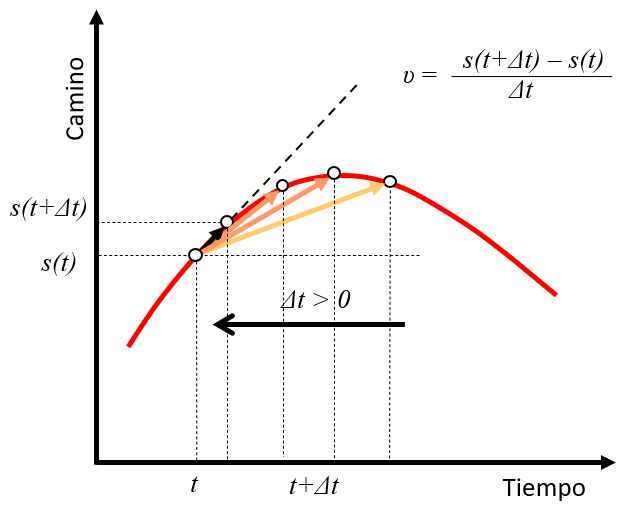
This generalizes what had already been seen for the case of constant velocity.

ID:(1638, 0)

Quote

The integral of the speed ($v$) corresponds to the area under the curve that defines this function. Therefore, the integral of the velocity between the start Time ($t_0$) and the time ($t$) corresponds to the distance traveled between the starting position ($s_0$) and the position ($s$).

Therefore, we have:



Which is represented in the following graph:

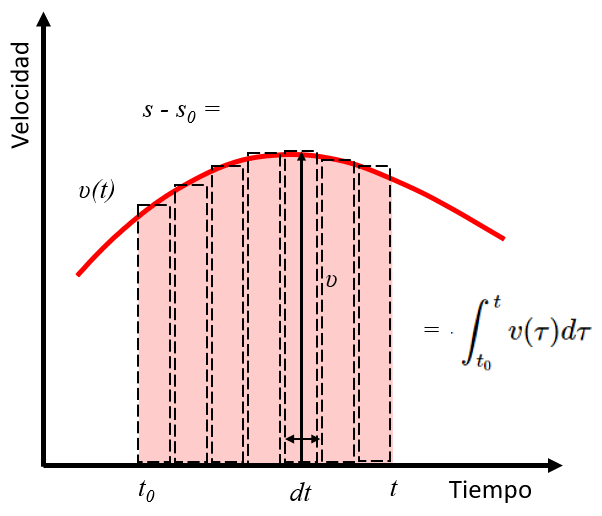
I walk as an area under the speed and time curve.

ID:(2242, 0)

Exercise

For motions occurring in more than one dimension, the description of motion in one dimension must be generalized. This is achieved by working with a multi-dimensional version for the position. In the case of three dimensions, this is:

$s \rightarrow \vec{s} = (x, y, z)$

Similarly, the derivative of the vector with respect to time can be defined, resulting in the velocity vector:

$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$

This is summarized in the following graphical representation:

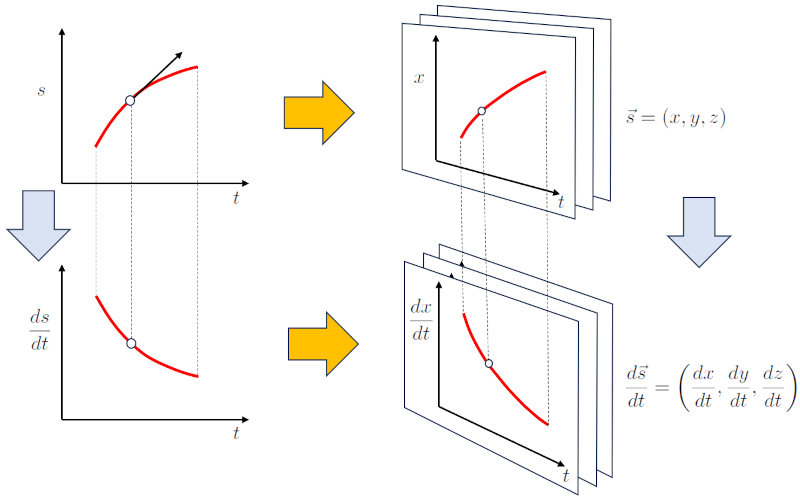
ID:(15506, 0)

Equation

In the case of one dimension, the speed ($v$) is related to the position ($s$) through its derivative at the time ($t$), while the integral of the speed ($v$) over the interval from the time ($t$) to the start Time ($t_0$) provides the position ($s$) from the starting position ($s_0$). In a more general context, in more than one dimension, the function the posición (vector) ($\vec{s}$) can be derived at the time ($t$), resulting in the speed (Vector) ($\vec{v}$)

ID:(15391, 0)