Usuario:
Aceleración angular instantanea
Storyboard 
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo.
La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular.
Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
ID:(1452, 0)
Aceleración angular instantanea
Storyboard
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo. La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular. Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Dado que la aceleraci n tangencial es
Si el versor del eje es $\hat{n}$ y el radial es $\hat{r}$, el versor tangencial puede calcularse mediante el producto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
En consecuencia, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
y
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deducir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
lo que se traduce en
Ejemplos
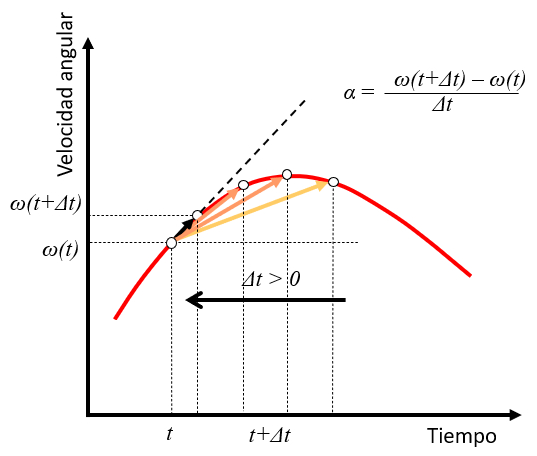
Si se toma un intervalo de tiempo $t$ con una velocidad angular $\omega(t)$ y se observa un punto en un momento futuro $t+\Delta t$ con una velocidad angular $\omega(t+\Delta t)$, la aceleraci n angular puede estimarse como la variaci n
$\omega(t+\Delta t)-\omega(t)$
en el transcurso del tiempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
A medida que el valor de $\Delta t$ disminuye, la aceleraci n toma el papel de la tangente a la curva de velocidad en ese momento:
Esto generaliza lo que ya se ha visto en el caso de la aceleraci n angular constante.
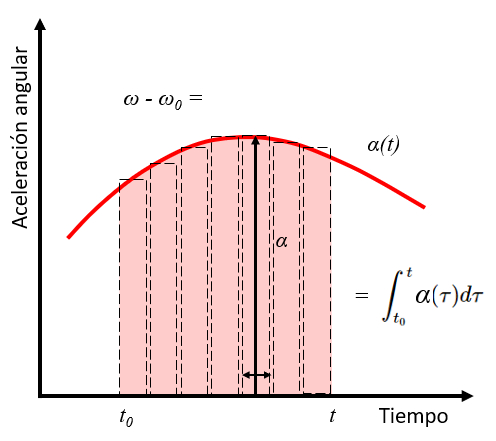
La integral de una funci n corresponde al rea bajo la curva que define dicha funci n. Por lo tanto, la integral de la aceleraci n angular entre los tiempos $t_0$ y $t$ corresponde a la variaci n de la velocidad angular entre la velocidad angular inicial $\omega_0$ y $\omega$.
Por lo tanto, utilizando
Lo cual se muestra en el siguiente gr fico:
La direcci n de la aceleraci n tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en direcci n al radio:
Al igual que en la aceleraci n de traslaci n, existe el concepto de aceleraci n angular instant nea, que es la aceleraci n angular con
que existe en un tiempo espec fico. Esto se calcula en la aproximaci n de intervalos de tiempo muy peque os $(\Delta t\rightarrow 0)$, es decir
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
donde
Si integramos en el tiempo la definici n de la velocidad angular con
lo que significa que para un intervalo de tiempo $dt$, el ngulo recorrido es:
$d\omega = \alpha dt$
Si consideramos $N$ intervalos $dt_i$ con velocidades angulares $\alpha_i$, el ngulo total recorrido ser :
$\omega - \omega_0 = \displaystyle\sum_i \alpha_i dt_i$
Si consideramos la curva de velocidad angular-tiempo, los elementos $\alpha_i dt_i$ corresponden a rect ngulos con altura $\alpha_i$ y ancho $dt_i$. La suma, por lo tanto, corresponde al rea bajo la curva de velocidad angular-tiempo. Por lo tanto, la suma se puede expresar como una integral utilizando
En general hay que entender la aceleraci n como un ente en tres dimensiones, es decir vectorial. Esto es su velocidad requiere ser descrita por un vector velocidad angular $\vec{\omega}$ para el cual se puede definir componente una aceleraci n con
con lo que se puede generalizar la aceleraci n con:
La integraci n de la definici n diferencial, es decir, de las variaciones temporales infinitesimales, con respecto a la ecuaci n
Podemos realizar la integraci n entre el tiempo $t_0$ y $t$ de la aceleraci n $a(\tau)$ para obtener la velocidad $v(t)$ si la velocidad inicial es $v_0$, utilizando la ecuaci n:
La aceleraci n angular se expresa como un vector en la direcci n del eje de rotaci n. Dado que el radio de rotaci n y la aceleraci n angular son perpendiculares a la aceleraci n tangencial, se obtiene la siguiente relaci n:
Esta relaci n puede escribirse como el producto cruz entre la aceleraci n angular y el radio, representado de la siguiente manera:
ID:(1452, 0)
