User: 
Instantaneous angular acceleration
Storyboard 
To describe how angular velocity evolves over time, one must examine its variation with respect to time.
The relationship of the change in angular velocity corresponds to the angular displacement covered over the elapsed time, which when divided by this time, yields the angular acceleration.
For an infinitesimally small time interval, the angular acceleration corresponds to the instantaneous angular acceleration.
ID:(1452, 0)
Angular acceleration as a derivative
Concept
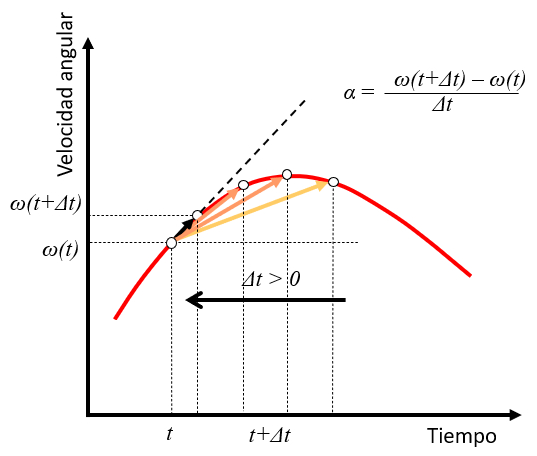
If a time t is taken with an angular velocity \omega(t) and a point is observed at a future time t+\Delta t with an angular velocity \omega(t+\Delta t), the angular acceleration can be estimated as the variation
\omega(t+\Delta t)-\omega(t)
over time \Delta t:
\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}
As the value of \Delta t decreases, the acceleration takes on the role of the tangent to the velocity curve at that time:
This generalizes what has already been seen for the case of constant angular acceleration.
ID:(11413, 0)
Angular Velocity as Integral of Acceleration
Description
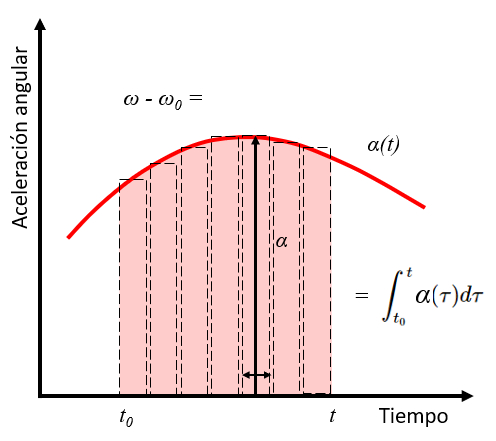
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of angular acceleration between the times t_0 and t corresponds to the change in angular velocity between the initial angular velocity \omega_0 and \omega.
Thus, using angular Speed rad/s, initial Angular Speed rad/s, instantaneous Angular Acceleration rad/s^2, start Time s and time s, we obtain:
| \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau |
This is illustrated in the following graph:
ID:(11415, 0)
Tangential acceleration, right hand rule
Image
The orientation of tangential acceleration can be obtained using the right-hand rule, with fingers pointing towards the axis and then rotating towards the radius:
ID:(11600, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
\vec{a} = \vec{\alpha} \times \vec{r}
&a = &alpha x &r
\vec{alpha} =\displaystyle\frac{d \vec{\omega} }{d t }
&alpha = d&omega / dt
\alpha =\displaystyle\frac{ d\omega }{ dt }
alpha = domega / dt
\omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau
omega = omega_0 + @INT( alpha, tau, t_0, t )
v = v_0 +\displaystyle\int_{t_0}^t a(\tau) d\tau
v = v_0 + integrate( a, tau, t_0, t )
ID:(15426, 0)
Instantaneous Angular Acceleration
Equation
Similar to translational acceleration, there is the concept of Instantaneous Angular Acceleration, which is the angular acceleration with
| \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t } |
that exists at a specific time. This is calculated in the approximation of very small time intervals (\Delta t\rightarrow 0), meaning
\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}
where
| \alpha =\displaystyle\frac{ d\omega }{ dt } |
ID:(3235, 0)
Angular acceleration integration
Equation
If we integrate the definition of angular velocity with respect to time, using instantaneous Angular Acceleration rad/s^2, instantaneous Angular Speed rad/s and time s, we obtain:
| \alpha =\displaystyle\frac{ d\omega }{ dt } |
This means that for a time interval dt, the traversed angle is given by:
d\omega = \alpha dt
If we consider N intervals dt_i with corresponding angular velocities \alpha_i, the total traversed angle will be:
\omega - \omega_0 = \sum_i \alpha_i dt_i
Considering the angular velocity-time curve, the elements \alpha_i dt_i correspond to rectangles with height \alpha_i and width dt_i. The sum, therefore, corresponds to the area under the angular velocity-time curve. Hence, the sum can be expressed as an integral using instantaneous Angular Acceleration rad/s^2, instantaneous Angular Speed rad/s and time s:
| \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau |
ID:(11416, 0)
Angular acceleration in more dimensions
Equation
En general, la aceleración debe entenderse como una entidad tridimensional, es decir, vectorial. Esto significa que su velocidad debe ser descrita por un vector de velocidad angular \vec{\omega}, para el cual se puede definir una componente de aceleración con instantaneous Angular Acceleration rad/s^2, instantaneous Angular Speed rad/s and time s
| \alpha =\displaystyle\frac{ d\omega }{ dt } |
De este modo, se puede generalizar la aceleración como:
| \vec{alpha} =\displaystyle\frac{d \vec{\omega} }{d t } |
ID:(6742, 0)
Angular acceleration integration
Equation
The integration of the differential definition, i.e., infinitesimal temporal variations, with respect to equation yields:
| a =\displaystyle\frac{ d v }{ d t } |
We can perform integration between time t_0 and t of the acceleration a(\tau) to obtain the velocity v(t) if the initial velocity is v_0, using the equation:
| v = v_0 +\displaystyle\int_{t_0}^t a(\tau) d\tau |
ID:(11414, 0)
Tangential acceleration, vector shape
Equation
Angular acceleration is represented as a vector aligned with the axis of rotation. Because the radius of rotation and angular acceleration are orthogonal to tangential acceleration, we have:
| a = r \alpha |
This relationship can be expressed as the cross product of angular acceleration and radius, written as:
| \vec{a} = \vec{\alpha} \times \vec{r} |
Given that the tangential acceleration is
| a = r \alpha |
If the unit vector of the axis is \hat{n} and the radial unit vector is \hat{r}, the tangential unit vector can be calculated using the cross product:
\hat{t} = \hat{n} \times \hat{r}
As a result, considering that
\vec{a} = a \hat{t}
,
\vec{r} = r \hat{r}
, and
\vec{\alpha} = \alpha \hat{n}
,
we can deduce that
\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}
,
which translates to
| \vec{a} = \vec{\alpha} \times \vec{r} |
.
ID:(11598, 0)