Utilizador:
Aceleração angular instantânea
Storyboard 
Para descrever como a velocidade angular evolui ao longo do tempo, é necessário estudar a variação desta em relação ao tempo.
A relação da variação da velocidade angular equivale à mudança na velocidade angular ao longo do tempo decorrido, que, quando dividida por esse tempo, corresponde à aceleração angular.
Para um intervalo de tempo infinitesimal, a aceleração angular corresponde à aceleração angular instantânea.
ID:(1452, 0)
Velocidade Angular como Integral da Aceleração
Nota
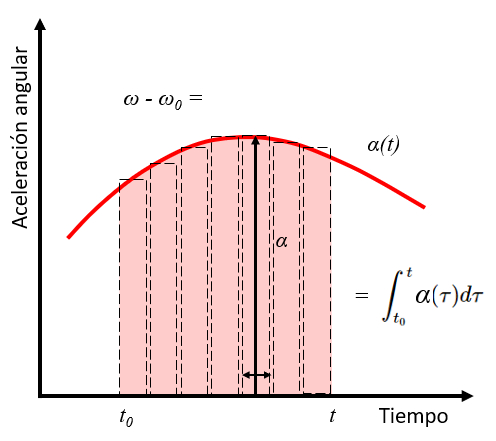
A integral de uma função corresponde à área sob a curva que define essa função. Portanto, a integral da aceleração angular entre os tempos $t_0$ e $t$ corresponde à variação da velocidade angular entre a velocidade angular inicial $\omega_0$ e $\omega$.
Assim, utilizando aceleração angular instantânea $rad/s^2$, tempo $s$, tempo inicial $s$, velocidade angular $rad/s$ e velocidade angular inicial $rad/s$, obtemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Isso é ilustrado no seguinte gráfico:
ID:(11415, 0)
Aceleração angular instantânea
Descrição
Para descrever como a velocidade angular evolui ao longo do tempo, é necessário estudar a variação desta em relação ao tempo. A relação da variação da velocidade angular equivale à mudança na velocidade angular ao longo do tempo decorrido, que, quando dividida por esse tempo, corresponde à aceleração angular. Para um intervalo de tempo infinitesimal, a aceleração angular corresponde à aceleração angular instantânea.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Dado que a acelera o tangencial
| $ a = r \alpha $ |
Se o vetor unit rio do eixo $\hat{n}$ e o vetor unit rio radial $\hat{r}$, o vetor unit rio tangencial pode ser calculado usando o produto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
Consequentemente, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
e
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deduzir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
o que se traduz em
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
.
(ID 11598)
Exemplos
(ID 15415)
Se um intervalo de tempo $t$ considerado com uma velocidade angular $\omega(t)$ e um ponto observado em um tempo futuro $t+\Delta t$ com uma velocidade angular $\omega(t+\Delta t)$, a acelera o angular pode ser estimada como a varia o
$\omega(t+\Delta t)-\omega(t)$
ao longo do tempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
medida que o valor de $\Delta t$ diminui, a acelera o assume o papel da tangente curva de velocidade naquele momento:
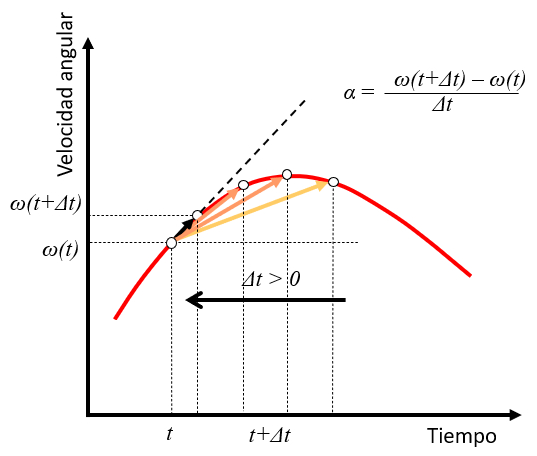
Isso generaliza o que j foi visto para o caso da acelera o angular constante.
(ID 11413)
A integral de uma fun o corresponde rea sob a curva que define essa fun o. Portanto, a integral da acelera o angular entre os tempos $t_0$ e $t$ corresponde varia o da velocidade angular entre a velocidade angular inicial $\omega_0$ e $\omega$.
Assim, utilizando aceleração angular instantânea $rad/s^2$, tempo $s$, tempo inicial $s$, velocidade angular $rad/s$ e velocidade angular inicial $rad/s$, obtemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Isso ilustrado no seguinte gr fico:
(ID 11415)
A orienta o da acelera o tangencial pode ser obtida utilizando a regra da m o direita, onde os dedos apontam em dire o ao eixo e depois giram em dire o ao raio:
(ID 11600)
(ID 15426)
ID:(1452, 0)