Storyboard

>Modelo

ID:(1428, 0)

Iframe

>Top

ID:(15492, 0)

Descrição

>Top

Se houver uma altura da coluna ($h$) de líquido com la densidade líquida ($\rho_w$) sob o efeito da gravidade, utilizando la aceleração gravitacional ($g$), é gerado ($$) conforme:

Este ($$) gera, através do tubo de saída com o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), um fluxo de um fluxo de volume 1 ($J_{V1}$) de acordo com a lei de Hagen-Poiseuille:

Como esta equação inclui la seção no ponto 2 ($S_2$), la densidade de fluxo 2 ($j_{s2}$) pode ser calculado através de:

Com isso, obtém-se:

que corresponde a uma velocidade média.

Para modelar o sistema, os parâmetros-chave são:

• Diâmetro interno do recipiente: 93 mm

• Diâmetro interno do canal de evacuação: 3,2 mm

• Comprimento do canal de evacuação: 18 mm

A altura inicial do líquido é de 25 cm.

ID:(9870, 0)

Descrição

>Top

Si analisarmos a equação

que descreve a aplicação de Hagen-Poiseuille, podemos observar que a curva só se ajusta aos dados experimentais nos seguintes casos:

A velocidade é baixa (quando a coluna está quase vazia)
O raio do canal de evacuação deve ser reduzido de 1,5 mm para 0,6 mm.

Isso indica que o fluxo é principalmente turbulento e que apenas em níveis de baixa velocidade a velocidade é suficientemente baixa para que o número de Reynolds seja baixo o suficiente para que o fluxo seja laminar.

ID:(11065, 0)

Descrição

>Top

Se o programa Tracker for utilizado, é possível medir a altura do menisco da coluna e o alcance do jato. A relação entre os dois é mostrada no seguinte gráfico:

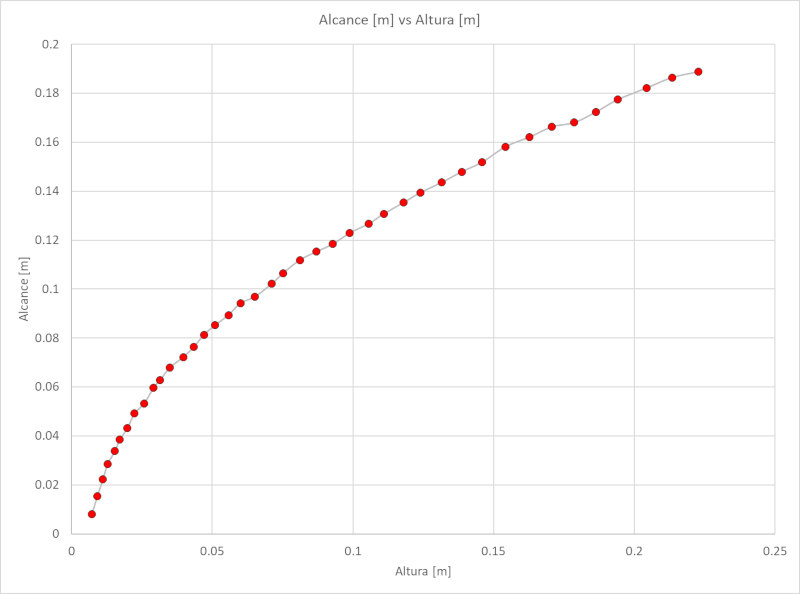
Os dados registrados, que podem ser baixados como uma tabela do Excel no seguinte link tabela do Excel, são os seguintes:

Nota: E é a notação científica (zB. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)

ID:(11062, 0)

Top

>Top

Parâmetros

$g$

g

Aceleração gravitacional

m/s^2

$\tau_{hp}$

tau_hp

Coluna de tempo característica com Hagen Pouseuille

s

$\rho_w$

rho_w

Densidade líquida

kg/m^3

$\pi$

pi

Pi

rad

$R$

R

Raio do tubo

m

$\eta$

eta

Viscosidade

Pa s

Variáveis

$h$

h

Altura da coluna

m

$h_0$

h_0

Altura inicial da coluna líquida

m

$\Delta L$

DL

Comprimento do tubo

m

$j_{s1}$

j_s1

Densidade de fluxo 1

m/s

$j_{s2}$

j_s2

Densidade de fluxo 2

m/s

$\Delta s$

Ds

Elemento de tubo

m

$J_{V1}$

J_V1

Fluxo de volume 1

m^3/s

$J_{V2}$

J_V2

Fluxo de volume 2

m^3/s

$r$

r

Raio do disco

m

$S_1$

S_1

Seção no ponto 1

m^2

$S_2$

S_2

Seção no ponto 2

m^2

$t$

t

Tempo

s

$\Delta t$

Dt

Tempo decorrido

s

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15494, 0)

Equação

>Top, >Modelo

O coluna de tempo característica com Hagen Pouseuille ($\tau_{hp}$) é calculado a partir de la aceleração gravitacional ($g$), la densidade líquida ($\rho_w$), o comprimento do tubo ($\Delta L$), o raio do tubo ($R$), la seção no ponto 2 ($S_2$) e la viscosidade ($\eta$) utilizando:

$\tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$\tau_{hp}$

Coluna de tempo característica com Hagen Pouseuille

$s$

10087

$\Delta L$

Comprimento do tubo

$m$

5430

$\rho_w$

Densidade líquida

$kg/m^3$

5407

$\pi$

Pi

3.1415927

$rad$

5057

$R$

Raio do tubo

$m$

5417

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

$\eta$

Viscosidade

$Pa s$

5422

Relação

Desenvolvimento

ID:(14521, 0)

Equação

>Top, >Modelo

Dado o modelo para o fluxo de um líquido viscoso através de um tubo, e considerando que a altura da coluna determina a pressão, podemos estimar la densidade de fluxo ($j_s$) em função de la altura da coluna ($h$), utilizando la aceleração gravitacional ($g$), la densidade líquida ($\rho_w$), o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$) da seguinte forma:

$j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h$

$j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$h$

Altura da coluna

$m$

5406

$\Delta L$

Comprimento do tubo

$m$

5430

$j_s$

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$\rho_w$

Densidade líquida

$kg/m^3$

5407

$R$

Raio do tubo

$m$

5417

$\eta$

Viscosidade

$Pa s$

5422

Relação

Desenvolvimento

Se considerarmos que o canal de drenagem apresenta resistência hidráulica, podemos modelá-lo com a equação de Hagen-Poiseuille:

$J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

onde a diferença de pressão é determinada pela coluna de água:

$p = \rho_w g h$

e a velocidade é obtida através do fluxo:

$j_s = \displaystyle\frac{ J_V }{ S }$

Dessa forma, obtemos a relação para o cálculo da velocidade em função da altura:

$j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h$

ID:(11064, 0)

Equação

>Top, >Modelo

La altura da coluna ($h$), como função de o tempo ($t$), apresenta um comportamento exponencial com la altura inicial da coluna líquida ($h_0$) e o coluna de tempo característica com Hagen Pouseuille ($\tau_{hp}$):

$h = h_0 e^{-t/\tau_{hp}}$

Condições

Variáveis

$h$

Altura da coluna

$m$

5406

$h_0$

Altura inicial da coluna líquida

$m$

10085

$\tau_{hp}$

Coluna de tempo característica com Hagen Pouseuille

$s$

10087

$t$

Tempo

$s$

5264

Relação

Desenvolvimento

Se na equação

$S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h$

as constantes forem substituídas por

$\tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$

obtemos a equação diferencial linear de primeira ordem

$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$

cuja solução é

$h = h_0 e^{-t/\tau_{hp}}$

ID:(14522, 0)

Equação

>Top, >Modelo

Uma das leis mais básicas na física é a conservação da massa, que é válida em todo o nosso mundo macroscópico. Apenas no mundo microscópico existe uma conversão entre massa e energia, a qual não consideraremos neste caso. No caso de um fluido, isso significa que a massa que entra por um tubo deve ser igual à que sai dele.

Se a densidade for constante, o mesmo se aplica ao volume. Nestes casos, quando tratamos o fluxo como um fluido incompressível, significa que um determinado volume que entra em uma extremidade do tubo deve sair pela outra extremidade. Isso pode ser expresso como a igualdade entre o fluxona posição 1 ($J_1$) e o fluxona posição 2 ($J_2$), com a equação:

$J_{V1} = J_{V2}$

Condições

Variáveis

$J_{V1}$

Fluxo de volume 1

$m^3/s$

8478

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

Relação

ID:(939, 0)

Equação

>Top, >Modelo

O princípio da continuidade determina que o fluxo no primeiro ponto, que é igual a la densidade de fluxo 1 ($j_{s1}$) vezes la seção no ponto 1 ($S_1$), deve ser igual ao fluxo no segundo ponto, dado por la densidade de fluxo 2 ($j_{s2}$) vezes la seção no ponto 2 ($S_2$). A partir disso, conclui-se que:

$S_1 j_{s1} = S_2 j_{s2}$

Condições

Variáveis

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$S_1$

Seção no ponto 1

$m^2$

5257

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

ID:(4350, 0)

Equação

>Top, >Modelo

La densidade de fluxo ($j_s$) está relacionado com la distância percorrida em um tempo ($\Delta s$), que é a distância que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:

$j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Condições

Variáveis

$j_s$

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$\Delta s$

Elemento de tubo

$m$

10291

$\Delta t$

Tempo decorrido

$s$

5103

Relação

ID:(4348, 0)

Equação

>Top, >Modelo

Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) através da seguinte fórmula:

$j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$

$j_s = \displaystyle\frac{ J_V }{ S }$

Condições

Variáveis

$j_s$

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$J_V$

$J_{V1}$

Fluxo de volume 1

$m^3/s$

8478

$S$

$S_1$

Seção no ponto 1

$m^2$

5257

Relação

Desenvolvimento

O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):

$\Delta V = S \Delta s$

Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:

$j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$

Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:

$j_s = \displaystyle\frac{ J_V }{ S }$

ID:(4349, 1)

Equação

>Top, >Modelo

Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) através da seguinte fórmula:

$j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$

$j_s = \displaystyle\frac{ J_V }{ S }$

Condições

Variáveis

$j_s$

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$J_V$

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

Desenvolvimento

O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):

$\Delta V = S \Delta s$

Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:

$j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$

Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:

$j_s = \displaystyle\frac{ J_V }{ S }$

ID:(4349, 2)

Equação

>Top, >Modelo

O fluxo de volume ($J_V$) pode ser calculado com a lei de Hagen-Poiseuille que com os parâmetros la viscosidade ($\eta$), la diferença de pressão ($\Delta p$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) é:

$J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Condições

Variáveis

$\Delta L$

Comprimento do tubo

$m$

5430

$J_V$

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

$\pi$

Pi

3.1415927

$rad$

5057

$R$

Raio do tubo

$m$

5417

$\eta$

Viscosidade

$Pa s$

5422

Relação

Desenvolvimento

Se considerarmos o perfil de velocidade em um raio do cilindro ($v$) para um fluido em um canal cilíndrico, onde la velocidade em um raio do cilindro ($v$) varia em relação a raio de posição em um tubo ($r$) de acordo com a seguinte expressão:

$v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$

envolvendo o raio do tubo ($R$) e la taxa de fluxo máxima ($v_{max}$). Podemos calcular la taxa de fluxo máxima ($v_{max}$) utilizando la viscosidade ($\eta$), la diferença de pressão ($\Delta p$) e o comprimento do tubo ($\Delta L$) da seguinte forma:

$v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

Se integrarmos a velocidade em toda a seção transversal do canal, obteremos o fluxo de volume ($J_V$), definida como a integral de $\pi r v(r)$ em relação a raio de posição em um tubo ($r$) de $0$ a raio do tubo ($R$). Essa integral pode ser simplificada da seguinte maneira:

$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$

A integração resulta na lei de Hagen-Poiseuille resultante:

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

ID:(3178, 0)

Equação

>Top, >Modelo

A diferença de altura, representada por la diferença de altura ($\Delta h$), implica que a pressão em ambas as colunas é diferente. Em particular, la diferença de pressão ($\Delta p$) é uma função de la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$) e la diferença de altura ($\Delta h$), da seguinte forma:

$\Delta p = \rho_w g h$

$\Delta p = \rho_w g \Delta h$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$\Delta h$

$h$

Altura da coluna

$m$

5406

$\rho_w$

Densidade líquida

$kg/m^3$

5407

Relação

Desenvolvimento

Se houver la diferença de pressão ($\Delta p$) entre dois pontos, conforme determinado pela equação:

$\Delta p = p_2 - p_1$

podemos usar la pressão da coluna de água ($p$), que é definida como:

$p_t = p_0 + \rho_w g h$

Isso resulta em:

$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$

Como la diferença de altura ($\Delta h$) é:

$\Delta h = h_2 - h_1$

la diferença de pressão ($\Delta p$) pode ser expressa como:

$\Delta p = \rho_w g \Delta h$

ID:(4345, 0)

Equação

>Top, >Modelo

La superfície de um disco ($S$) de um raio do disco ($r$) é calculada da seguinte forma:

$S_1 = \pi r ^2$

$S = \pi r ^2$

Condições

Variáveis

$\pi$

Pi

3.1415927

$rad$

5057

$r$

Raio do disco

$m$

5275

$S$

$S_1$

Seção no ponto 1

$m^2$

5257

Relação

ID:(3804, 1)

Equação

>Top, >Modelo

La superfície de um disco ($S$) de um raio do disco ($r$) é calculada da seguinte forma:

$S_2 = \pi R ^2$

$S = \pi r ^2$

Condições

Variáveis

$\pi$

Pi

3.1415927

$rad$

5057

$r$

$R$

Raio do tubo

$m$

5417

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

ID:(3804, 2)