User:
Column casting in laminar form
Storyboard 
It is considered a column with water with a hole in its lower part. The emptying is monitored obtaining an output speed depending on the height of the column.
If the data is modeled with Bernoulli but the exit through the hole is modeled with Hagen Poiseville, which corrects the problem of the case in which it was assumed without viscosity.
ID:(1428, 0)
Liquid column exit velocity
Description
If there is a column height ($h$) of liquid with the liquid density ($\rho_w$) under the effect of gravity, using the gravitational Acceleration ($g$), the variación de la Presión ($\Delta p$) is generated according to:
| $ \Delta p = \rho_w g h $ |
This the variación de la Presión ($\Delta p$) produces a flow through the outlet tube with the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$) of a volume flow 1 ($J_{V1}$) according to the Hagen-Poiseuille law:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Since this equation includes the section in point 2 ($S_2$), the flux density 2 ($j_{s2}$) can be calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
With this, we obtain:
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
which corresponds to an average velocity.
To model the system, the key parameters are:
• Interior diameter of the container: 93 mm
• Interior diameter of the evacuation channel: 3.2 mm
• Length of the evacuation channel: 18 mm
The initial liquid height is 25 cm.
ID:(9870, 0)
Decrease in the level of the liquid column
Description
If we analyze the equation
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
which describes the application of Hagen-Poiseuille, we observe that the curve only matches the experimental data under the following conditions:
The velocity is low (when the column is nearly empty).
The radius of the evacuation channel must be reduced from 1.5 mm to 0.6 mm.
This shows that the flow is primarily turbulent and that only at low velocity levels is the velocity low enough for the Reynolds number to be low and the flow to be laminar.
ID:(11065, 0)
Column Emptying Experiment: Height and Reach
Description
If the Tracker program is used, the height of the meniscus of the column and the range of the jet can be measured. The relationship between the two is shown in the following graph:
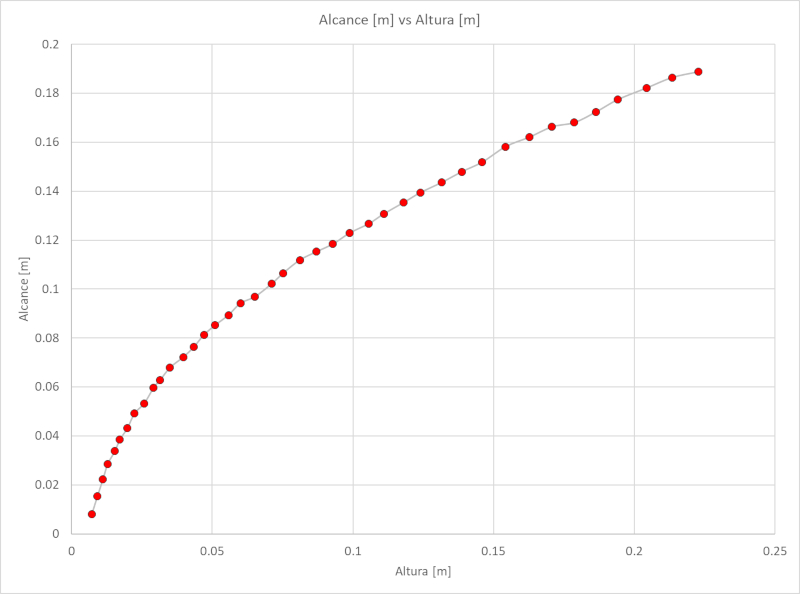
Reach [m] vs Height [m]
The recorded data, which can be downloaded as an Excel table from the following link excel table, are as follows:
| Time [s] | Height [m] | Reach [m] |
| 0 | 2.23E-01 | 1.89E-01 |
| 4 | 2.14E-01 | 1.86E-01 |
| 8 | 2.04E-01 | 1.82E-01 |
| 12 | 1.94E-01 | 1.77E-01 |
| 16 | 1.86E-01 | 1.72E-01 |
| 20 | 1.79E-01 | 1.68E-01 |
| 24 | 1.71E-01 | 1.66E-01 |
| 28 | 1.63E-01 | 1.62E-01 |
| 32 | 1.54E-01 | 1.58E-01 |
| 36 | 1.46E-01 | 1.52E-01 |
| 40 | 1.39E-01 | 1.48E-01 |
| 44 | 1.32E-01 | 1.44E-01 |
| 48 | 1.24E-01 | 1.39E-01 |
| 52 | 1.18E-01 | 1.35E-01 |
| 56 | 1.11E-01 | 1.31E-01 |
| 60 | 1.06E-01 | 1.27E-01 |
| 64 | 9.88E-02 | 1.23E-01 |
| 68 | 9.29E-02 | 1.18E-01 |
| 72 | 8.70E-02 | 1.15E-01 |
| 76 | 8.11E-02 | 1.12E-01 |
| 80 | 7.52E-02 | 1.06E-01 |
| 84 | 7.12E-02 | 1.02E-01 |
| 88 | 6.51E-02 | 9.69E-02 |
| 92 | 6.00E-02 | 9.42E-02 |
| 96 | 5.58E-02 | 8.94E-02 |
| 100 | 5.09E-02 | 8.52E-02 |
| 104 | 4.70E-02 | 8.13E-02 |
| 108 | 4.34E-02 | 7.63E-02 |
| 112 | 3.97E-02 | 7.22E-02 |
| 116 | 3.49E-02 | 6.79E-02 |
| 120 | 3.15E-02 | 6.28E-02 |
| 124 | 2.91E-02 | 5.96E-02 |
| 128 | 2.58E-02 | 5.33E-02 |
| 132 | 2.23E-02 | 4.92E-02 |
| 136 | 1.98E-02 | 4.31E-02 |
| 140 | 1.71E-02 | 3.85E-02 |
| 144 | 1.54E-02 | 3.38E-02 |
| 148 | 1.28E-02 | 2.85E-02 |
| 152 | 1.11E-02 | 2.23E-02 |
| 156 | 9.17E-03 | 1.54E-02 |
| 160 | 7.15E-03 | 7.95E-03 |
Note: E indicates scientific notation (ej. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)
ID:(11062, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $
j_s = rho_w * g * R ^2* h /(8* eta * l )
$ \Delta p = \rho_w g h $
Dp = rho_w * g * Dh
$h = h_0 e^{-t/\tau_{hp}}$
h = h_0 *exp(- t / tau_hp )
$ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$
J_V =- pi * R ^4* Dp /(8* eta * DL )
$ J_{V1} = J_{V2} $
J_V1 = J_V2
$ S_1 = \pi r ^2$
S = pi * r ^2
$ S_2 = \pi R ^2$
S = pi * r ^2
$ S_1 j_{s1} = S_2 j_{s2} $
S_1 * j_s1 = S_2 * j_s2
$ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$
tau_hp = (8* eta * DL * S )/( pi * R ^4 * rho * g * h )
ID:(15494, 0)
Characteristic time column with viscous liquid
Equation
The characteristic time column with Hagen Pouseuille ($\tau_{hp}$) is calculated from the gravitational Acceleration ($g$), the liquid density ($\rho_w$), the tube length ($\Delta L$), the tube radius ($R$), the section in point 2 ($S_2$), and the viscosity ($\eta$) using:
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
ID:(14521, 0)
Column emptying experiment: Model with Hagen Poiseuille
Equation
Given the model for the flow of a viscous liquid through a tube, and considering that the height of the column determines the pressure, we can estimate the flux density ($j_s$) as a function of the column height ($h$), using the gravitational Acceleration ($g$), the liquid density ($\rho_w$), the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$) through:
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
If we consider that the drainage channel presents hydraulic resistance, we can model it using the Hagen-Poiseuille equation:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
where the pressure difference is determined by the water column:
| $ p = \rho_w g h $ |
and the velocity is obtained through the flow:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
In this way, we obtain the relationship for calculating the velocity as a function of height:
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
ID:(11064, 0)
Temporal evolution of the viscous liquid column
Equation
The column height ($h$), as a function of the time ($t$), exhibits an exponential behavior involving the initial height of liquid column ($h_0$) and the characteristic time column with Hagen Pouseuille ($\tau_{hp}$):
| $h = h_0 e^{-t/\tau_{hp}}$ |
If in the equation
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
the constants are replaced by
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
we obtain the first-order linear differential equation
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$
whose solution is
| $h = h_0 e^{-t/\tau_{hp}}$ |
ID:(14522, 0)
Volume conservation
Equation
One of the most basic laws in physics is the conservation of mass, which holds true throughout our macroscopic world. Only in the microscopic world does a conversion between mass and energy exist, which we will not consider in this case. In the case of a fluid, this means that the mass entering through a pipe must be equal to the mass exiting it.
If density is constant, the same applies to volume. In such cases, when we treat the flow as an incompressible fluid, it means that a given volume entering one end of the pipe must exit the other end. This can be expressed as the equality between the flow in Position 1 ($J_1$) and the flow in Position 2 ($J_2$), with the equation:
| $ J_{V1} = J_{V2} $ |
ID:(939, 0)
Continuity by section
Equation
The principle of continuity dictates that the flow at the first point, which is equal to the flux density 1 ($j_{s1}$) times the section in point 1 ($S_1$), must be equal to the flow at the second point, given by the flux density 2 ($j_{s2}$) times the section in point 2 ($S_2$). From this, it follows that:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(4350, 0)
Average flow density
Equation
The flux density ($j_s$) is related to the distance traveled in a time ($\Delta s$), which is the distance that the fluid travels in the time elapsed ($\Delta t$), as follows:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 0)
Volume Flow and its Speed (1)
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Volume Flow and its Speed (2)
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Hagen Poiseuille Equation
Equation
The volume flow ($J_V$) can be calculated with the Hagen-Poiseuille law that with the parameters the viscosity ($\eta$), the pressure difference ($\Delta p$), the tube radius ($R$) and the tube length ($\Delta L$) is:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
If we consider the profile of speed on a cylinder radio ($v$) for a fluid in a cylindrical channel, where the speed on a cylinder radio ($v$) varies with respect to radius of position in a tube ($r$) according to the following expression:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
involving the tube radius ($R$) and the maximum flow rate ($v_{max}$). We can calculate the maximum flow rate ($v_{max}$) using the viscosity ($\eta$), the pressure difference ($\Delta p$), and the tube length ($\Delta L$) as follows:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
If we integrate the velocity across the cross-section of the channel, we obtain the volume flow ($J_V$), defined as the integral of $\pi r v(r)$ with respect to radius of position in a tube ($r$) from $0$ to tube radius ($R$). This integral can be simplified as follows:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
The integration yields the resulting Hagen-Poiseuille law:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(3178, 0)
Pressure difference between columns
Equation
The height difference, denoted by the height difference ($\Delta h$), implies that the pressure in both columns is distinct. In particular, the pressure difference ($\Delta p$) is a function of the liquid density ($\rho_w$), the gravitational Acceleration ($g$), and the height difference ($\Delta h$), as follows:
| $ \Delta p = \rho_w g h $ |
| $ \Delta p = \rho_w g \Delta h $ |
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ \Delta p = p_2 - p_1 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)
Surface of a disk (1)
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S_1 = \pi r ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Surface of a disk (2)
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S_2 = \pi R ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)