Benützer: 
Laminarer Säulenauslauf
Storyboard 
Es handelt sich um einen Wassersäule mit einem Loch im unteren Teil. Das Entleeren wird überwacht, wobei eine Ausgabegeschwindigkeit abhängig von der Höhe der Säule erhalten wird.
Wenn die Daten mit Bernoulli modelliert werden, der Ausgang durch das Loch jedoch mit Hagen Poiseville modelliert wird, wird das Problem des Falls behoben, in dem angenommen wurde, dass es keine Viskosität gibt.
ID:(1428, 0)
Austrittsgeschwindigkeit der Flüssigkeitssäule
Beschreibung
Wenn man eine Höhe der Säule ($h$) Flüssigkeit mit die Flüssigkeitsdichte ($\rho_w$) unter dem Einfluss der Schwerkraft hat, wird mit die Gravitationsbeschleunigung ($g$) eine die Variación de la Presión ($\Delta p$) gemäß folgender Gleichung erzeugt:
| $ \Delta p = \rho_w g h $ |
Diese die Variación de la Presión ($\Delta p$) führt durch das Auslassrohr mit der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) zu einem Fluss von ein Volumenstrom 1 ($J_{V1}$) gemäß dem Hagen-Poiseuille-Gesetz:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Da diese Gleichung die Abschnitt in Punkt 2 ($S_2$) enthält, kann die Flussdichte 2 ($j_{s2}$) berechnet werden mittels:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Damit erhält man:
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
was einer mittleren Geschwindigkeit entspricht.
Um das System zu modellieren, sind die Schlüsseldaten:
• Innendurchmesser des Behälters: 93 mm
• Innendurchmesser des Abflusskanals: 3,2 mm
• Länge des Abflusskanals: 18 mm
Die anfängliche Flüssigkeitshöhe beträgt 25 cm.
ID:(9870, 0)
Absinken des Niveaus der Flüssigkeitssäule
Beschreibung
Wenn wir die Gleichung
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
analysieren, die die Anwendung von Hagen-Poiseuille beschreibt, stellen wir fest, dass die Kurve nur mit den experimentellen Daten in folgenden Fällen übereinstimmt:
Die Geschwindigkeit ist niedrig (wenn die Säule fast leer ist).
Der Radius des Evakuierungskanals muss von 1,5 mm auf 0,6 mm reduziert werden.
Dies zeigt, dass der Fluss hauptsächlich turbulent ist und dass nur bei niedrigen Geschwindigkeiten die Geschwindigkeit niedrig genug ist, damit die Reynolds-Zahl niedrig ist und der Fluss laminar ist.
ID:(11065, 0)
Experiment zum Entleeren von Säulen: Höhe und Reichweite
Beschreibung
Wenn das Tracker-Programm verwendet wird, können die Höhe des Meniskus der Säule und die Reichweite des Strahls gemessen werden. Das Verhältnis zwischen beiden wird im folgenden Diagramm dargestellt:
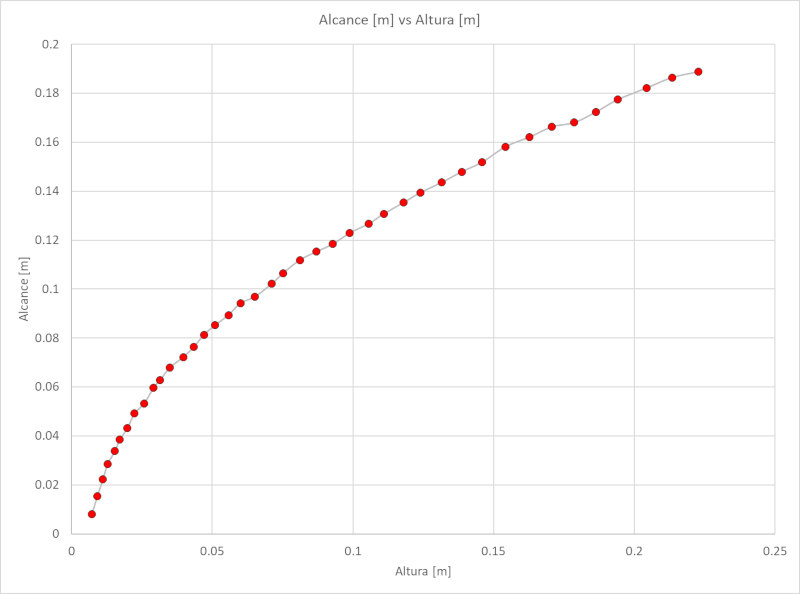
Reichweite [m] vs Höhe [m]
Die aufgezeichneten Daten, die als Excel-Tabelle unter folgendem Link heruntergeladen werden können Excel-Tabelle, lauten wie folgt:
| Zeit [s] | Höhe [m] | Weite [m] |
| 0 | 2.23E-01 | 1.89E-01 |
| 4 | 2.14E-01 | 1.86E-01 |
| 8 | 2.04E-01 | 1.82E-01 |
| 12 | 1.94E-01 | 1.77E-01 |
| 16 | 1.86E-01 | 1.72E-01 |
| 20 | 1.79E-01 | 1.68E-01 |
| 24 | 1.71E-01 | 1.66E-01 |
| 28 | 1.63E-01 | 1.62E-01 |
| 32 | 1.54E-01 | 1.58E-01 |
| 36 | 1.46E-01 | 1.52E-01 |
| 40 | 1.39E-01 | 1.48E-01 |
| 44 | 1.32E-01 | 1.44E-01 |
| 48 | 1.24E-01 | 1.39E-01 |
| 52 | 1.18E-01 | 1.35E-01 |
| 56 | 1.11E-01 | 1.31E-01 |
| 60 | 1.06E-01 | 1.27E-01 |
| 64 | 9.88E-02 | 1.23E-01 |
| 68 | 9.29E-02 | 1.18E-01 |
| 72 | 8.70E-02 | 1.15E-01 |
| 76 | 8.11E-02 | 1.12E-01 |
| 80 | 7.52E-02 | 1.06E-01 |
| 84 | 7.12E-02 | 1.02E-01 |
| 88 | 6.51E-02 | 9.69E-02 |
| 92 | 6.00E-02 | 9.42E-02 |
| 96 | 5.58E-02 | 8.94E-02 |
| 100 | 5.09E-02 | 8.52E-02 |
| 104 | 4.70E-02 | 8.13E-02 |
| 108 | 4.34E-02 | 7.63E-02 |
| 112 | 3.97E-02 | 7.22E-02 |
| 116 | 3.49E-02 | 6.79E-02 |
| 120 | 3.15E-02 | 6.28E-02 |
| 124 | 2.91E-02 | 5.96E-02 |
| 128 | 2.58E-02 | 5.33E-02 |
| 132 | 2.23E-02 | 4.92E-02 |
| 136 | 1.98E-02 | 4.31E-02 |
| 140 | 1.71E-02 | 3.85E-02 |
| 144 | 1.54E-02 | 3.38E-02 |
| 148 | 1.28E-02 | 2.85E-02 |
| 152 | 1.11E-02 | 2.23E-02 |
| 156 | 9.17E-03 | 1.54E-02 |
| 160 | 7.15E-03 | 7.95E-03 |
Hinweis: E ist wissenschaftliche Notation (zB. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)
ID:(11062, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $
j_s = rho_w * g * R ^2* h /(8* eta * l )
$ \Delta p = \rho_w g h $
Dp = rho_w * g * Dh
$h = h_0 e^{-t/\tau_{hp}}$
h = h_0 *exp(- t / tau_hp )
$ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$
J_V =- pi * R ^4* Dp /(8* eta * DL )
$ J_{V1} = J_{V2} $
J_V1 = J_V2
$ S_1 = \pi r ^2$
S = pi * r ^2
$ S_2 = \pi R ^2$
S = pi * r ^2
$ S_1 j_{s1} = S_2 j_{s2} $
S_1 * j_s1 = S_2 * j_s2
$ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$
tau_hp = (8* eta * DL * S )/( pi * R ^4 * rho * g * h )
ID:(15494, 0)
Charakteristische Zeitsäule mit viskoser Flüssigkeit
Gleichung
Der Charakteristische Zeitsäule mit Hagen Pouseuille ($\tau_{hp}$) wird aus die Gravitationsbeschleunigung ($g$), die Flüssigkeitsdichte ($\rho_w$), der Rohrlänge ($\Delta L$), der Rohrradius ($R$), die Abschnitt in Punkt 2 ($S_2$) und die Viskosität ($\eta$) berechnet mittels:
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
ID:(14521, 0)
Experiment zum Entleeren von Säulen: Model mit Hagen Poiseuille
Gleichung
Angesichts des Modells für den Fluss einer viskosen Flüssigkeit durch ein Rohr und der Tatsache, dass die Höhe der Säule den Druck bestimmt, können wir die Flussdichte ($j_s$) in Abhängigkeit von die Höhe der Säule ($h$) unter Verwendung von die Gravitationsbeschleunigung ($g$), die Flüssigkeitsdichte ($\rho_w$), der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) wie folgt abschätzen:
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
Wenn wir davon ausgehen, dass der Entwässerungskanal einen hydraulischen Widerstand aufweist, können wir ihn mit der Hagen-Poiseuille-Gleichung modellieren:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
wobei der Druckunterschied durch die Wassersäule bestimmt wird:
| $ p = \rho_w g h $ |
und die Geschwindigkeit durch den Durchfluss bestimmt wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Auf diese Weise erhalten wir die Beziehung zur Berechnung der Geschwindigkeit in Abhängigkeit von der Höhe:
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
ID:(11064, 0)
Zeitliche Entwicklung der viskosen Flüssigkeitssäule
Gleichung
Die Höhe der Säule ($h$) als Funktion von der Zeit ($t$) zeigt ein exponentielles Verhalten mit die Anfangshöhe der Flüssigkeitssäule ($h_0$) und der Charakteristische Zeitsäule mit Hagen Pouseuille ($\tau_{hp}$):
| $h = h_0 e^{-t/\tau_{hp}}$ |
Wenn in der Gleichung
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
die Konstanten durch
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
ersetzt werden, erhalten wir die lineare Differentialgleichung erster Ordnung
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$
deren Lösung lautet
| $h = h_0 e^{-t/\tau_{hp}}$ |
ID:(14522, 0)
Volumen Erhaltung
Gleichung
Eine der grundlegendsten Gesetze in der Physik ist die Erhaltung der Masse, die in unserer makroskopischen Welt gilt. Nur in der mikroskopischen Welt existiert eine Umwandlung zwischen Masse und Energie, die wir in diesem Fall nicht berücksichtigen werden. Im Falle eines Fluids bedeutet dies, dass die Masse, die durch ein Rohr eintritt, gleich der Masse sein muss, die es verlässt.
Wenn die Dichte konstant ist, gilt dasselbe für das Volumen. In solchen Fällen, wenn wir den Fluss als ein inkompressibles Fluid behandeln, bedeutet dies, dass ein bestimmtes Volumen, das an einem Ende des Rohrs eintritt, am anderen Ende austreten muss. Dies kann als Gleichheit zwischen der Fließen in Position 1 ($J_1$) und der Fließen in Position 2 ($J_2$) ausgedrückt werden, mit der Gleichung:
| $ J_{V1} = J_{V2} $ |
ID:(939, 0)
Kontinuität nach Abschnitten
Gleichung
Das Kontinuitätsprinzip besagt, dass der Fluss am ersten Punkt, der gleich die Flussdichte 1 ($j_{s1}$) mal die Abschnitt in Punkt 1 ($S_1$) ist, dem Fluss am zweiten Punkt entsprechen muss, der durch die Flussdichte 2 ($j_{s2}$) mal die Abschnitt in Punkt 2 ($S_2$) gegeben ist. Daraus folgt:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(4350, 0)
Durchschnittliche Strömungsdichte
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$), was die Strecke ist, die die Flüssigkeit in der Abgelaufene Zeit ($\Delta t$) zurücklegt, wie folgt:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 0)
Volumenstrom und seine Geschwindigkeit (1)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Volumenstrom und seine Geschwindigkeit (2)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Hagen Poiseuille-Gleichung
Gleichung
Der Volumenstrom ($J_V$) lässt sich mit dem Hagen-Poiseuille-Gesetz berechnen, das mit den Parametern die Viskosität ($\eta$), die Druckunterschied ($\Delta p$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) lautet:
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Wenn wir das Profil von Geschwindigkeit auf einer Zylinder-Radio ($v$) für ein Fluid in einem zylindrischen Kanal betrachten, in dem die Geschwindigkeit auf einer Zylinder-Radio ($v$) in Abhängigkeit von Positionsradius in einem Rohr ($r$) gemäß folgendem Ausdruck variiert:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
unter Verwendung von der Rohrradius ($R$) und die Maximale Durchflussrate ($v_{max}$). Können wir die Maximale Durchflussrate ($v_{max}$) mithilfe von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und der Rohrlänge ($\Delta L$) wie folgt berechnen:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Wenn wir die Geschwindigkeit über den Querschnitt des Kanals integrieren, erhalten wir der Volumenstrom ($J_V$), definiert als das Integral von $\pi r v(r)$ bezüglich Positionsradius in einem Rohr ($r$) von $0$ bis Rohrradius ($R$). Dieses Integral kann wie folgt vereinfacht werden:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
Die Integration führt zur resultierenden Hagen-Poiseuille-Gesetz:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(3178, 0)
Druckunterschied zwischen Säulen
Gleichung
Der Höhenunterschied, dargestellt durch die Höhendifferenz ($\Delta h$), bedeutet, dass der Druck in beiden Säulen unterschiedlich ist. Insbesondere ist die Druckunterschied ($\Delta p$) eine Funktion von die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Höhendifferenz ($\Delta h$), wie folgt:
| $ \Delta p = \rho_w g h $ |
| $ \Delta p = \rho_w g \Delta h $ |
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ \Delta p = p_2 - p_1 $ |
können wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedrückt werden:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)
Oberfläche einer Scheibe (1)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_1 = \pi r ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Oberfläche einer Scheibe (2)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_2 = \pi R ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)