Utilisateur:
Vitesse de sortie de la colonne liquide
Description 
Si lon a une hauteur de la colonne ($h$) de liquide avec a densité du liquide ($\rho_w$) sous leffet de la gravité, en utilisant a accélération gravitationnelle ($g$), on génère ($$) selon :
| $ \Delta p = \rho_w g h $ |
Cette ($$) produit un débit à travers le tube de sortie avec le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$) de un volumique flux 1 ($J_{V1}$) conformément à la loi de Hagen-Poiseuille :
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Étant donné que cette équation inclut a section au point 2 ($S_2$), a densité de flux 2 ($j_{s2}$) peut être calculé via :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Avec cela, on obtient :
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
ce qui correspond à une vitesse moyenne.
Pour modéliser le système, les paramètres clés sont :
• Diamètre intérieur du récipient : 93 mm
• Diamètre intérieur du canal dévacuation : 3,2 mm
• Longueur du canal dévacuation : 18 mm
La hauteur initiale du liquide est de 25 cm.
ID:(9870, 0)
Diminution du niveau de la colonne de liquide
Description
Si nous analysons l'équation
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
qui décrit l'application de Hagen-Poiseuille, nous constatons que la courbe ne correspond qu'aux données expérimentales dans les cas suivants :
La vitesse est faible (lorsque la colonne est presque vide).
Le rayon du canal d\'évacuation doit être réduit de 1,5 mm à 0,6 mm.
Cela montre que l\'écoulement est principalement turbulent et que seule à des niveaux de faible vitesse, la vitesse est suffisamment basse pour que le nombre de Reynolds soit faible et que l\'écoulement soit laminaire.
ID:(11065, 0)
Column casting experiment: height and reach
Description
Si le programme Tracker est utilisé, il est possible de mesurer la hauteur du ménisque de la colonne et la portée du jet. La relation entre les deux est représentée dans le graphique suivant :
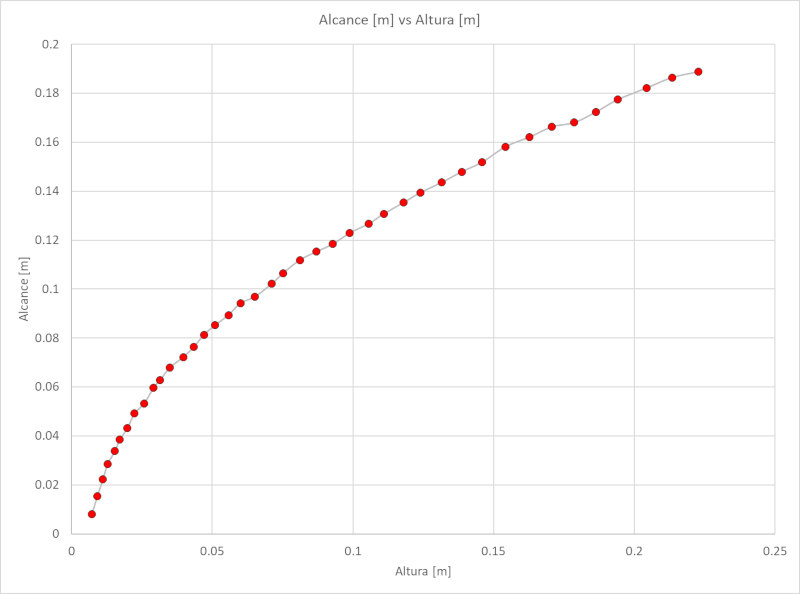
Les données enregistrées, qui peuvent être téléchargées sous forme de tableau Excel depuis le lien suivant tableau Excel, sont les suivantes :
| Zeit [s] | Höhe [m] | Weite [m] |
| 0 | 2.23E-01 | 1.89E-01 |
| 4 | 2.14E-01 | 1.86E-01 |
| 8 | 2.04E-01 | 1.82E-01 |
| 12 | 1.94E-01 | 1.77E-01 |
| 16 | 1.86E-01 | 1.72E-01 |
| 20 | 1.79E-01 | 1.68E-01 |
| 24 | 1.71E-01 | 1.66E-01 |
| 28 | 1.63E-01 | 1.62E-01 |
| 32 | 1.54E-01 | 1.58E-01 |
| 36 | 1.46E-01 | 1.52E-01 |
| 40 | 1.39E-01 | 1.48E-01 |
| 44 | 1.32E-01 | 1.44E-01 |
| 48 | 1.24E-01 | 1.39E-01 |
| 52 | 1.18E-01 | 1.35E-01 |
| 56 | 1.11E-01 | 1.31E-01 |
| 60 | 1.06E-01 | 1.27E-01 |
| 64 | 9.88E-02 | 1.23E-01 |
| 68 | 9.29E-02 | 1.18E-01 |
| 72 | 8.70E-02 | 1.15E-01 |
| 76 | 8.11E-02 | 1.12E-01 |
| 80 | 7.52E-02 | 1.06E-01 |
| 84 | 7.12E-02 | 1.02E-01 |
| 88 | 6.51E-02 | 9.69E-02 |
| 92 | 6.00E-02 | 9.42E-02 |
| 96 | 5.58E-02 | 8.94E-02 |
| 100 | 5.09E-02 | 8.52E-02 |
| 104 | 4.70E-02 | 8.13E-02 |
| 108 | 4.34E-02 | 7.63E-02 |
| 112 | 3.97E-02 | 7.22E-02 |
| 116 | 3.49E-02 | 6.79E-02 |
| 120 | 3.15E-02 | 6.28E-02 |
| 124 | 2.91E-02 | 5.96E-02 |
| 128 | 2.58E-02 | 5.33E-02 |
| 132 | 2.23E-02 | 4.92E-02 |
| 136 | 1.98E-02 | 4.31E-02 |
| 140 | 1.71E-02 | 3.85E-02 |
| 144 | 1.54E-02 | 3.38E-02 |
| 148 | 1.28E-02 | 2.85E-02 |
| 152 | 1.11E-02 | 2.23E-02 |
| 156 | 9.17E-03 | 1.54E-02 |
| 160 | 7.15E-03 | 7.95E-03 |
Remarque : E est la notation scientifique (zB. 1.2E+3 = 1.2x10^3 = 1200, y 1.2E-3 = 1.2x10^-3 = 0.0012)
ID:(11062, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $
j_s = rho_w * g * R ^2* h /(8* eta * l )
$ \Delta p = \rho_w g h $
Dp = rho_w * g * Dh
$h = h_0 e^{-t/\tau_{hp}}$
h = h_0 *exp(- t / tau_hp )
$ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$
J_V =- pi * R ^4* Dp /(8* eta * DL )
$ J_{V1} = J_{V2} $
J_V1 = J_V2
$ S_1 = \pi r ^2$
S = pi * r ^2
$ S_2 = \pi R ^2$
S = pi * r ^2
$ S_1 j_{s1} = S_2 j_{s2} $
S_1 * j_s1 = S_2 * j_s2
$ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$
tau_hp = (8* eta * DL * S )/( pi * R ^4 * rho * g * h )
ID:(15494, 0)
Colonne de temps caractéristique avec liquide visqueux
Équation
Le colonne horaire caractéristique avec Hagen Pouseuille ($\tau_{hp}$) est calculé à partir de a accélération gravitationnelle ($g$), a densité du liquide ($\rho_w$), le longueur du tube ($\Delta L$), le rayon du tube ($R$), a section au point 2 ($S_2$) et a viscosité ($\eta$) à l'aide de :
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
ID:(14521, 0)
Expérience de coulée de colonne: modèle avec Hagen Poiseuille
Équation
Étant donné le modèle pour l'écoulement d'un liquide visqueux à travers un tube, et en tenant compte du fait que la hauteur de la colonne détermine la pression, nous pouvons estimer a densité de flux ($j_s$) en fonction de a hauteur de la colonne ($h$), en utilisant a accélération gravitationnelle ($g$), a densité du liquide ($\rho_w$), le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$) comme suit :
| $ j_{s2} = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
Si nous considérons que le canal de drainage présente une résistance hydraulique, nous pouvons le modéliser avec l'équation de Hagen-Poiseuille :
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
où la différence de pression est déterminée par la colonne d'eau :
| $ p = \rho_w g h $ |
et la vitesse est obtenue à travers le débit :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
De cette manière, nous obtenons la relation pour calculer la vitesse en fonction de la hauteur :
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
ID:(11064, 0)
Evolution temporelle de la colonne de liquide visqueux
Équation
A hauteur de la colonne ($h$), en fonction de le temps ($t$), présente un comportement exponentiel avec a hauteur initiale de la colonne de liquide ($h_0$) et le colonne horaire caractéristique avec Hagen Pouseuille ($\tau_{hp}$) :
| $h = h_0 e^{-t/\tau_{hp}}$ |
Si dans l'équation
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
les constantes sont remplacées par
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
nous obtenons l'équation différentielle linéaire du premier ordre
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$
dont la solution est
| $h = h_0 e^{-t/\tau_{hp}}$ |
ID:(14522, 0)
Débit volumique instantané
Équation
L'une des lois les plus fondamentales en physique est la conservation de la masse, qui est valable dans tout notre monde macroscopique. Seul le monde microscopique connaît une conversion entre masse et énergie, que nous ne considérerons pas dans ce cas. Dans le cas d'un fluide, cela signifie que la masse entrant par un tuyau doit être égale à celle qui en sort.
Si la densité est constante, cela s'applique également au volume. Dans de tels cas, lorsque nous traitons l'écoulement comme un fluide incompressible, cela signifie qu'un volume donné entrant par une extrémité du tuyau doit sortir par l'autre extrémité. Cela peut être exprimé par l'égalité entre le flux en position 1 ($J_1$) et le flux en position 2 ($J_2$), avec l'équation :
| $ J_{V1} = J_{V2} $ |
ID:(939, 0)
Débit volumique instantané
Équation
Le principe de continuité stipule que le débit au premier point, égal à A densité de flux 1 ($j_{s1}$) multiplié par a section au point 1 ($S_1$), doit être égal au débit au second point, donné par a densité de flux 2 ($j_{s2}$) multiplié par a section au point 2 ($S_2$). Il en résulte que :
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(4350, 0)
Densité de flux moyenne
Équation
A densité de flux ($j_s$) est lié à A distance parcourue en un temps ($\Delta s$), qui est la distance parcourue par le fluide dans le temps écoulé ($\Delta t$), comme suit :
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 0)
Flux volumique et sa vitesse (1)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Flux volumique et sa vitesse (2)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_{s1} =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Loi de Hagen Poiseuille
Équation
Le volumique flux ($J_V$) peut être calculé avec la loi de Hagen-Poiseuille qui avec les paramètres a viscosité ($\eta$), a différence de pression ($\Delta p$), le rayon du tube ($R$) et le longueur du tube ($\Delta L$) est :
| $ J_{V2} =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Si nous examinons le profil de vitesse dans un rayon du cylindre ($v$) pour un fluide dans un canal cylindrique, où A vitesse dans un rayon du cylindre ($v$) varie en fonction de rayon de position dans un tube ($r$) selon l'expression suivante :
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
avec le rayon du tube ($R$) et a vitesse maximal ($v_{max}$). Nous pouvons calculer a vitesse maximal ($v_{max}$) en utilisant a viscosité ($\eta$), a différence de pression ($\Delta p$), et le longueur du tube ($\Delta L$) comme suit :
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Si nous intégrons la vitesse sur toute la section transversale du canal, nous obtenons le volumique flux ($J_V$), défini comme l'intégrale de $\pi r v(r)$ par rapport à rayon de position dans un tube ($r$) de $0$ à rayon du tube ($R$). Cette intégrale peut être simplifiée comme suit :
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
L'intégration donne la loi de Hagen-Poiseuille résultante :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(3178, 0)
Différence de pression entre les colonnes
Équation
La différence de hauteur, représentée par a différence de hauteur ($\Delta h$), implique que la pression dans les deux colonnes est différente. En particulier, a différence de pression ($\Delta p$) est une fonction de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), et a différence de hauteur ($\Delta h$), comme suit :
| $ \Delta p = \rho_w g h $ |
| $ \Delta p = \rho_w g \Delta h $ |
S'il existe a différence de pression ($\Delta p$) entre deux points, comme le détermine l'équation :
| $ \Delta p = p_2 - p_1 $ |
nous pouvons utiliser a pression de la colonne d'eau ($p$), qui est définie comme suit :
| $ p_t = p_0 + \rho_w g h $ |
Cela donne :
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Comme a différence de hauteur ($\Delta h$) est définie comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de pression ($\Delta p$) peut être exprimée comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)
Surface d'un disque (1)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_1 = \pi r ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Surface d'un disque (2)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_2 = \pi R ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)