Utilizador:
Medição de viscosidade
Descrição
Se uma pequena esfera de raio $a$ é deixada cair em um meio com viscosidade $\eta$, ela acelerará até que a força gravitacional,
$mg=\displaystyle\frac{4\pi}{3}a^3\rho_sg$
onde $\rho_s$ é a densidade do material da esfera, seja igualada pela força viscosa,
$6\pi \eta a v$
sendo $v$ a velocidade.
Portanto, é possível estimar a viscosidade do meio medindo a velocidade, uma vez que a equação é satisfeita:
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
onde o raio pode ser medido diretamente.
Aqui você pode observar o comportamento da esfera:
ID:(9871, 0)
Experimento de despejo de coluna
Descrição
Isso significa que à medida que a coluna vai esvaziando e a altura $h$ diminui, a velocidade $v$ também diminui de forma proporcional.
Os parâmetros-chave são:
• Diâmetro interno do recipiente: 93 mm
• Diâmetro interno do canal de evacuação: 3 mm
• Comprimento do canal de evacuação: 18 mm
Esses parâmetros são importantes para compreender e analisar o processo de esvaziamento da coluna e como a velocidade de saída varia com a altura.
ID:(9870, 0)
Experimento de esvaziamento de coluna: efeito de viscosidade
Descrição
Si analisarmos a equação
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
que descreve a aplicação de Hagen-Poiseuille, podemos observar que a curva só se ajusta aos dados experimentais nos seguintes casos:
A velocidade é baixa (quando a coluna está quase vazia)
O raio do canal de evacuação deve ser reduzido de 1,5 mm para 0,6 mm.
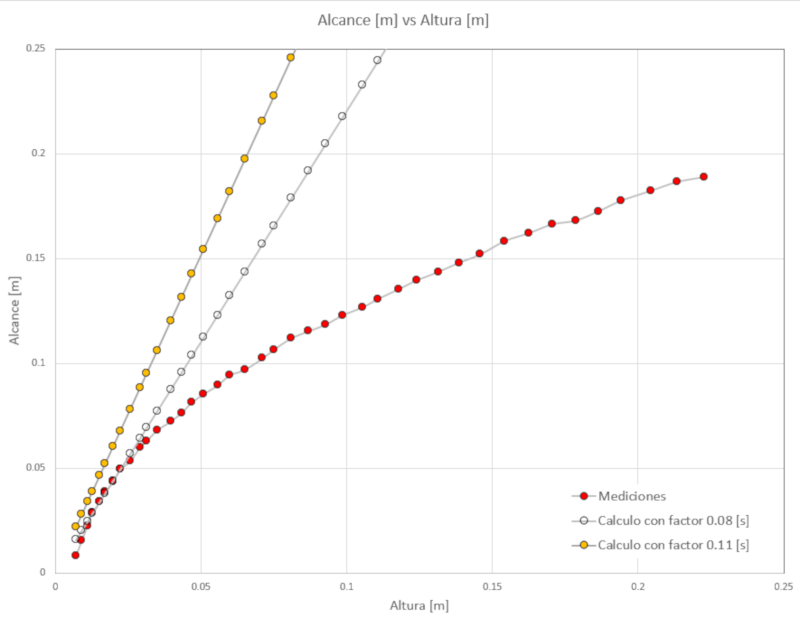
Isso indica que o fluxo é principalmente turbulento e que apenas em níveis de baixa velocidade a velocidade é suficientemente baixa para que o número de Reynolds seja baixo o suficiente para que o fluxo seja laminar.
ID:(11065, 0)
Cálculo de viscosidade
Imagem
Observando o percurso percorrido pela esfera ao longo do tempo, podemos ver que em grande parte ela se move a uma velocidade constante de cerca de 0,31 metros em 25 segundos, ou seja, 0,0124 m/s.
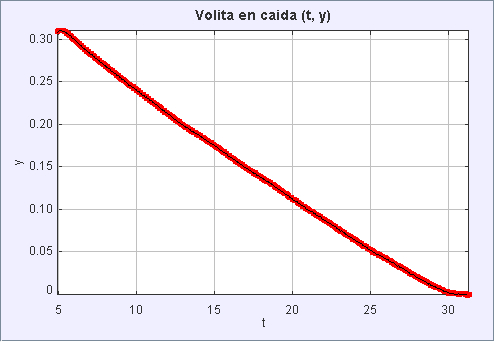
Ao rearranjarmos a igualdade entre a força gravitacional e a força de resistência de Stokes:
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
obtemos:
$\eta = \displaystyle\frac{2 a^2\rho_sg}{9 v}$
Considerando que a esfera tem um raio de 2 mm e pesa 8 mg, podemos determinar sua densidade como sendo aproximadamente $\rho_s\sim 2,38 g/cm^3$. Com isso, obtemos que a viscosidade é aproximadamente $\eta\sim 1,67 Pas$.
ID:(9881, 0)
Modelo
Conceito
Variáveis
Parâmetros
Parâmetro selecionado
Cálculos
Equação
$h = h_0 e^{-t/\tau_{hp}}$
h = h_0 *exp(- t / tau_hp )
$ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $
S *DIFF(h,t,1) = - pi * R ^4 * rho * g * h /(8* eta * DL )
$ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$
S*DIFF(h,t,1) = pi * R ^2*sqrt(2* g * h )
$ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$
tau_hp = (8* eta * DL * S )/( pi * R ^4 * rho * g * h )
$ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $
v = rho * g * R ^2* h /(8* eta * l )
ID:(15494, 0)
Coluna de tempo característica com líquido viscoso
Equação
Se observarmos a equação para o escoamento de uma coluna de líquido viscoso:
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
podemos condensar as constantes em uma unidade de tempo característica:
 $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
Este valor se torna um tempo característico para o escoamento de uma coluna com área de seção transversal $S$ de um líquido viscoso com viscosidade $\eta$, à medida que ele flui por um tubo de raio $R$.
ID:(14521, 0)
Altura da coluna de líquido não viscoso ao longo do tempo
Equação
No caso de um líquido não viscoso fluindo de forma laminar, a diferença de pressão gerada pela coluna é a seguinte:
| $ \Delta p = \rho_w g \Delta h $ |
Isso resulta em um fluxo de velocidade $v$ através de um tubo de acordo com o princípio de Bernoulli:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Dada a velocidade e o raio do tubo, podemos calcular o fluxo, que está relacionado com o fluxo dentro da coluna através da lei da continuidade. Por sua vez, isso se relaciona com a variação da altura $h", como descrito em:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
Usando a equação de Bernoulli, podemos analisar o caso de uma coluna de água que gera uma diferença de pressão:
| $ \Delta p = \rho_w g \Delta h $ |
e induz um fluxo de velocidade $v$ através de um tubo, de acordo com:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Portanto, podemos estimar a velocidade como:
$v = \sqrt{2 g h}$
Essa velocidade, através de uma seção de tubo com raio $R$, resulta em um fluxo:
$J = \pi R^2 v$
Se a coluna tem uma área de seção transversal $S$ e sua altura diminui em relação à variação da altura $h$ ao longo do tempo $t$, podemos aplicar a lei da continuidade, que estabelece:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
Portanto, a equação que descreve essa situação é:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
ID:(9882, 0)
Experimento de esvaziamento de coluna: modelo com Bernoulli
Descrição
Vamos considerar o sistema de um balde cilíndrico com um orifício de drenagem. Quando o tampão é removido, a água começa a fluir de acordo com a pressão existente. De acordo com o princípio de Bernoulli, dentro do balde ($v\sim 0$), a velocidade é zero, e temos:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$
enquanto fora do balde ($h=0$), apenas a componente cinética existe:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$
Como ambas as expressões são iguais, temos:
$\displaystyle\frac{1}{2}\rho v^2=\rho g h$
o que nos dá a velocidade como:
$v=\sqrt{2 g h}$
Para comparar com o experimento, podemos usar essa expressão para estimar, com:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
a distância que o jato de água deveria percorrer. Se plotarmos graficamente, observamos:
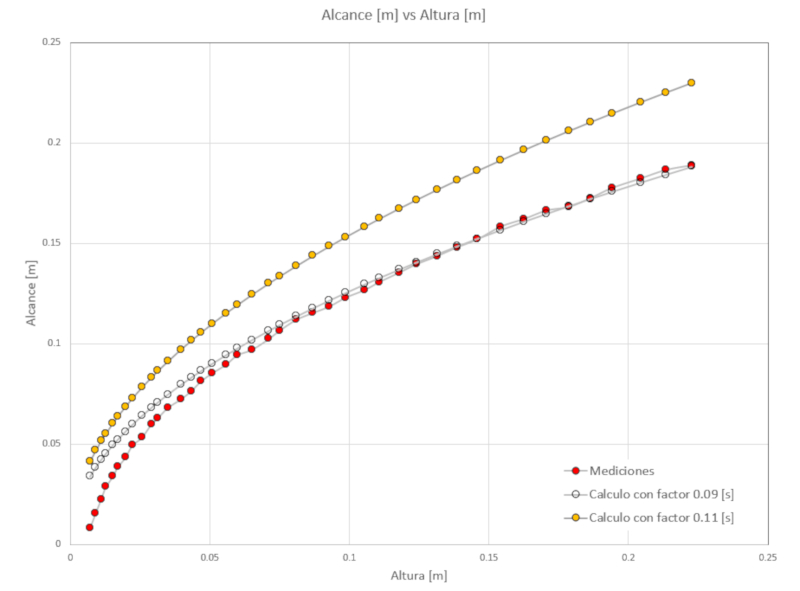
onde:
• os pontos vermelhos correspondem às medições experimentais,
• os pontos azuis correspondem à distância calculada usando um fator de 0,11,
• os pontos transparentes correspondem à distância calculada usando um fator de 0,09.
Portanto, podemos concluir que o modelo de Bernoulli superestima a velocidade com que o balde se esvazia. Isso ocorre porque na região do orifício de drenagem, os efeitos da viscosidade não são negligenciáveis, e, portanto, a velocidade é menor.
ID:(11063, 0)
Experimento de Fundição de Colunas: Modelo com Hagen Poiseuille
Equação
Dado o modelo para o fluxo de um líquido viscoso através de um tubo e considerando que a altura da coluna determina a pressão, podemos estimar a velocidade em função da altura da coluna:
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
Se considerarmos que o canal de drenagem apresenta resistência hidráulica, podemos modelá-lo com a equação de Hagen-Poiseuille:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
onde a diferença de pressão é determinada pela coluna de água:
| $ p = \rho_w g h $ |
e a velocidade é obtida através do fluxo:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Dessa forma, obtemos a relação para o cálculo da velocidade em função da altura:
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
ID:(11064, 0)
Altura da coluna de líquido viscoso ao longo do tempo
Equação
O fluxo laminar de um fluido com viscosidade $\eta$ através de um tubo de raio $R$ é descrito pela lei de Hagen-Poiseuille:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
A diferença de pressão é determinada pela altura da coluna $\Delta h$:
| $ \Delta p = \rho_w g \Delta h $ |
que diminui à medida que o líquido flui para fora. Ao aplicarmos a equação de continuidade, podemos demonstrar que a altura diminui ao longo do tempo da seguinte maneira:
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
Se o fluxo através do tubo é descrito pela equação:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
e a diferença de pressão $\Delta p$ é proporcional à altura da coluna $\Delta h = h:
| $ \Delta p = \rho_w g \Delta h $ |
podemos aplicar a conservação do fluxo $J_{V1}=J_V$ entre o tubo e a coluna $J_{V2}$:
| $ J_{V1} = J_{V2} $ |
,
onde o fluxo na coluna $J_{V2}$ com área de seção transversal $S$ é dado por:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Aqui, a densidade de fluxo $j_s$ corresponde à velocidade média, que é igual à taxa de variação da altura ao longo do tempo:
$j_s = \displaystyle\frac{dh}{dt}$
Dessa forma, obtemos a equação para a altura da coluna em função do tempo:
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
ID:(14520, 0)
Evolução temporal da coluna de líquido viscoso
Equação
A equação que descreve a evolução da coluna de líquido viscoso que está drenando é a seguinte:
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
Podemos reescrever esta equação usando o tempo característico:
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
Após a integração, obtemos:
| $h = h_0 e^{-t/\tau_{hp}}$ |
Se na equação
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
as constantes forem substituídas por
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
obtemos a equação diferencial linear de primeira ordem
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$
cuja solução é
| $h = h_0 e^{-t/\tau_{hp}}$ |
onde $h_0$ representa a altura inicial.
ID:(14522, 0)