Relativistic effects
Storyboard 
Relativistic effects occur at speeds close to the speed of light, that is, the parameters that are measured in a system traveling at a given speed give different results than those measured in a system at rest. In particular the lengths of the objects are reduced and the time intervals are lengthened as the mass increases. However, the load of the bodies is not affected.
ID:(1587, 0)
Electric field in a system at rest
Definition 
In the case of a system of plates moving horizontally, the electric field will depend on the surface charge density on the plates:

ID:(11787, 0)
Electric field in a moving system
Image 
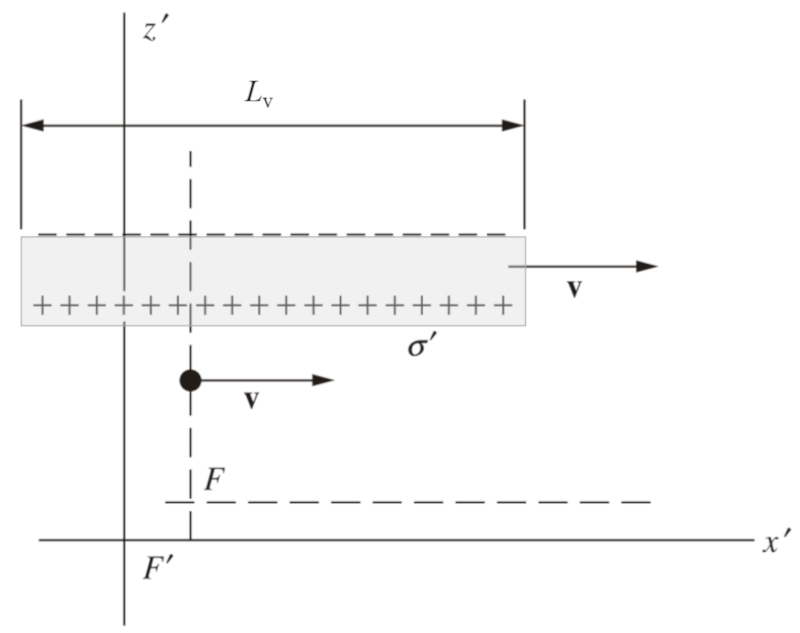
If the plates are in motion, their horizontal length will contract due to the effects of relativity. Although charges are not affected by the motion, the charge concentration per unit area will increase as the plates contract. This increase in charge concentration per area will result in an increase in the electric field between the plates:
ID:(11788, 0)
Argument for charge independence of movement
Note 
In Gauss's law, the choice of the surface around the charge is arbitrary. This means that when a charge moves, one can always find a Gaussian surface such that its integral remains unchanged. According to this law, it implies that the charge itself will not change:
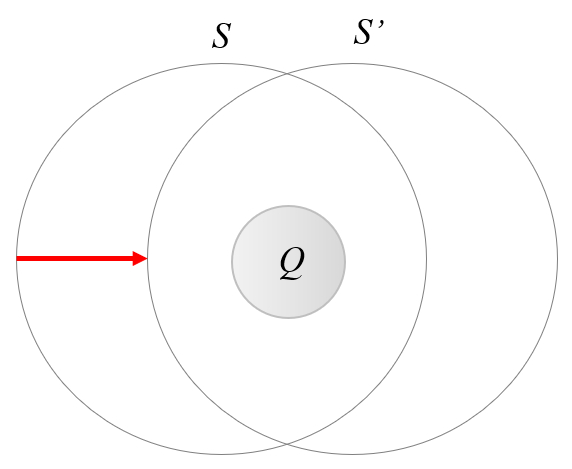
Therefore:
Electric charges are independent of the velocity at which the system moves.
ID:(11793, 0)
Gedankenexperiment on mass and charge
Quote 
A 'Gedankenexperiment' (thought experiment) that can be conducted involves imagining a box with two charges fixed to an arm that rotates. The theory of relativity implies that due to the motion, its mass will increase. If we hang this box from a dynamometer (a kind of market scale), it will extend, indicating a greater weight. However, the electric field measured outside the box will not have changed:
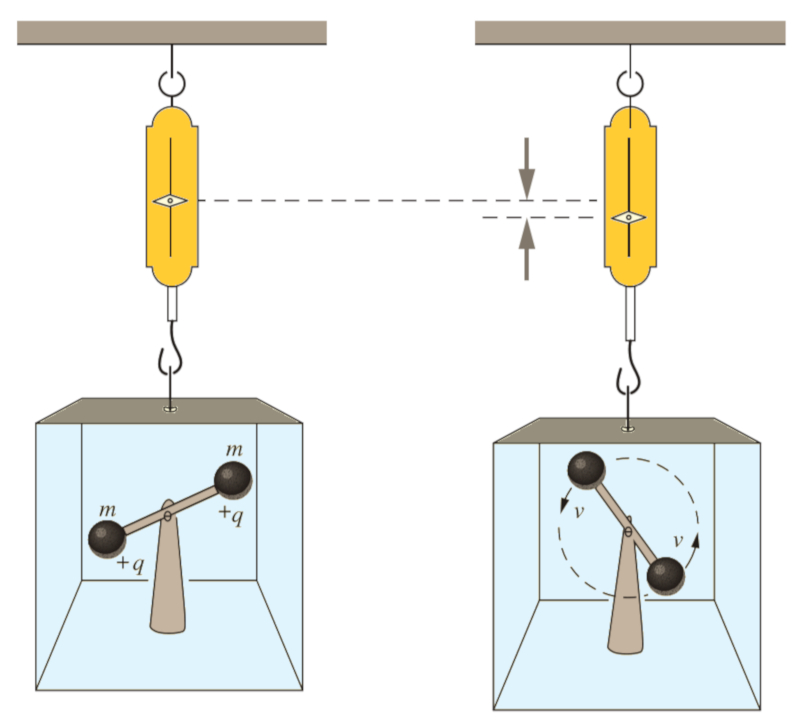
The concept of 'Gedankenexperiment' (thought experiment) was introduced by Einstein to facilitate the deduction of various laws of special relativity.
ID:(11794, 0)
Relativistic effects
Description 
Relativistic effects occur at speeds close to the speed of light, that is, the parameters that are measured in a system traveling at a given speed give different results than those measured in a system at rest. In particular the lengths of the objects are reduced and the time intervals are lengthened as the mass increases. However, the load of the bodies is not affected.
Variables
Calculations
Calculations
Equations
Examples
In the case of a system of plates moving horizontally, the electric field will depend on the surface charge density on the plates:

(ID 11787)
If the plates are in motion, their horizontal length will contract due to the effects of relativity. Although charges are not affected by the motion, the charge concentration per unit area will increase as the plates contract. This increase in charge concentration per area will result in an increase in the electric field between the plates:

(ID 11788)
In Gauss's law, the choice of the surface around the charge is arbitrary. This means that when a charge moves, one can always find a Gaussian surface such that its integral remains unchanged. According to this law, it implies that the charge itself will not change:

Therefore:
Electric charges are independent of the velocity at which the system moves.
(ID 11793)
Given that the charge density is defined as:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
and the cross-sectional area $S$ contracts in the direction of motion as described by:
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
we can calculate the relative charge density as:
| $ \sigma_v = \gamma \sigma_0 $ |
It's important to note that this relationship holds true only if the charge does not vary with the motion of the system.
(ID 11789)
As the electric field between two plates is described by the equations:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
In the relativistic case, the charge density per unit area is represented by the following equation:
| $ \sigma_v = \gamma \sigma_0 $ |
Therefore, we can conclude that the electric field experiences an increase in its magnitude, as given by the expression:
| $ E_{d,v} = \gamma E_{d,0} $ |
(ID 11790)
Considering that the force experienced by a test charge is described by:
| $ F = q E $ |
and the second law of Newton in its general form (in terms of momentum $p$ rather than acceleration) is expressed as:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
we can conclude that the equation of motion in a stationary system is:
| $ \displaystyle\frac{dp}{dt} = q E $ |
(ID 11791)
In the relativistic case, the electric field is given by:
| $ E_{d,v} = \gamma E_{d,0} $ |
coupled with the equation of motion:
| $ \displaystyle\frac{dp}{dt} = q E $ |
and the definition of momentum:
| $ p = m_i v $ |
This implies that for the dynamics to remain invariant under relativistic transformations, the mass must depend on the velocity of the system in the following manner:
| $ m_v = \gamma m_0 $ |
(ID 11792)
A 'Gedankenexperiment' (thought experiment) that can be conducted involves imagining a box with two charges fixed to an arm that rotates. The theory of relativity implies that due to the motion, its mass will increase. If we hang this box from a dynamometer (a kind of market scale), it will extend, indicating a greater weight. However, the electric field measured outside the box will not have changed:

The concept of 'Gedankenexperiment' (thought experiment) was introduced by Einstein to facilitate the deduction of various laws of special relativity.
(ID 11794)
ID:(1587, 0)
