Benützer:
Relativistische Effekte
Storyboard 
Relativistische Effekte treten bei Geschwindigkeiten nahe der Lichtgeschwindigkeit auf, dh die Parameter, die in einem System gemessen werden, das sich mit einer bestimmten Geschwindigkeit bewegt, ergeben andere Ergebnisse als diejenigen, die in einem System in Ruhe gemessen werden. Insbesondere werden die Längen der Objekte verringert und die Zeitintervalle mit zunehmender Masse verlängert. Die Belastung der Körper wird jedoch nicht beeinflusst.
ID:(1587, 0)
Elektrisches Feld in einem ruhenden System
Bild
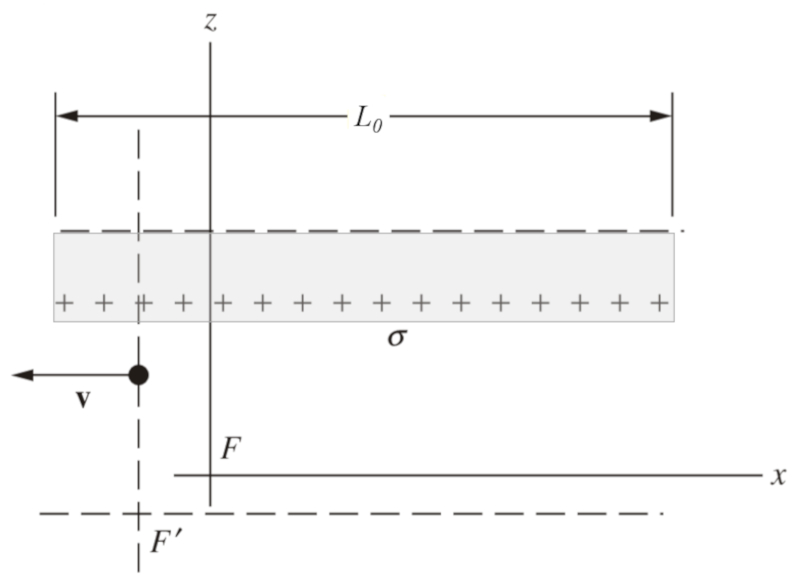
Im Fall eines Systems von Platten, die sich horizontal bewegen, hängt das elektrische Feld von der Flächenladungsdichte auf den Platten ab:
ID:(11787, 0)
Elektrisches Feld in einem bewegten System
Bild
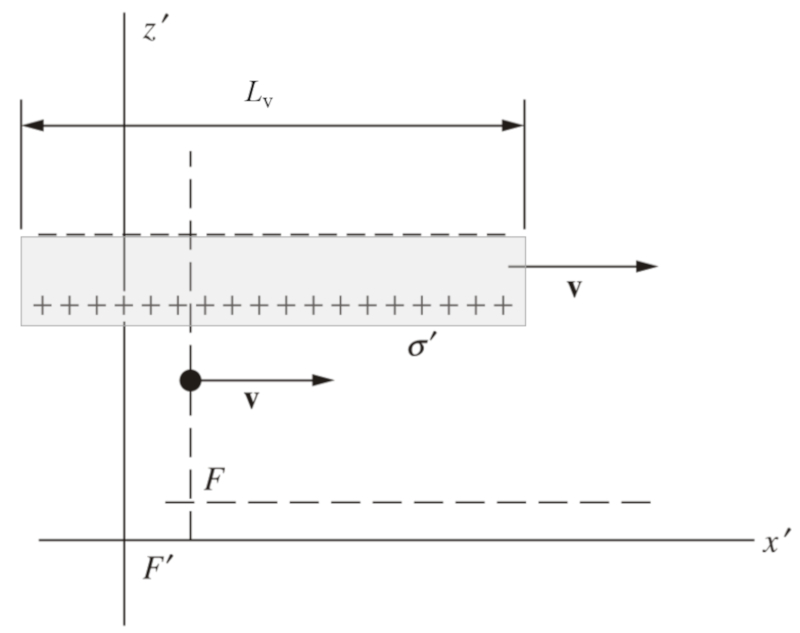
Wenn sich die Platten bewegen, wird ihre horizontale Länge aufgrund der relativistischen Effekte verkürzt. Obwohl die Ladungen von der Bewegung nicht beeinflusst werden, wird die Ladungskonzentration pro Flächeneinheit aufgrund der Kontraktion der Platten erhöht. Diese Zunahme der Ladungskonzentration pro Fläche führt zu einer Zunahme des elektrischen Feldes zwischen den Platten:
ID:(11788, 0)
Argument für die Ladungsunabhängigkeit der Bewegung
Bild
In Gaussschem Gesetz ist die Wahl der Oberfläche um die Ladung herum willkürlich. Dies bedeutet, dass bei einer Bewegung einer Ladung immer eine Gaußsche Fläche gefunden werden kann, sodass ihr Integral unverändert bleibt. Gemäß diesem Gesetz bedeutet dies, dass die Ladung selbst sich nicht ändern wird:
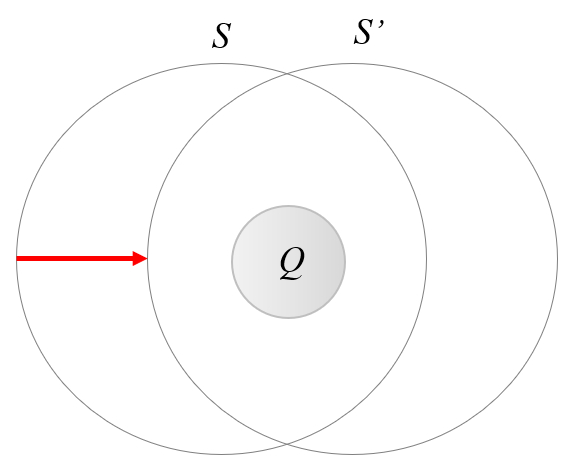
Daher:
Elektrische Ladungen sind unabhängig von der Geschwindigkeit, mit der sich das System bewegt.
ID:(11793, 0)
Relativistische Ladungsdichte
Gleichung
Da die Ladungsdichte definiert ist als:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
und der Querschnitt $S$ in Richtung der Bewegung schrumpft, wie durch:
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
beschrieben, können wir die relative Ladungsdichte wie folgt berechnen:
 $ \sigma_v = \gamma \sigma_0 $ |
Es ist wichtig zu beachten, dass diese Beziehung nur dann gültig ist, wenn die Ladung sich nicht mit der Bewegung des Systems ändert.
ID:(11789, 0)
Relativistisches elektrisches Feld
Gleichung
Certainly, here's an improved version of the text in German while keeping the code lines intact and maintaining the specified text length:
"Da das elektrische Feld zwischen zwei Platten durch die folgenden Gleichungen beschrieben wird:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
Im relativistischen Fall wird die Ladungsdichte pro Flächeneinheit durch die folgende Gleichung dargestellt:
| $ \sigma_v = \gamma \sigma_0 $ |
Daher können wir schlussfolgern, dass das elektrische Feld an Intensität zunimmt, wie durch den Ausdruck gegeben:
| $ E_{d,v} = \gamma E_{d,0} $ |
ID:(11790, 0)
Bewegungsgleichung in einem System in Ruhe
Gleichung
Angesichts der Tatsache, dass die von einer Testladung erfahrene Kraft wie folgt beschrieben wird:
| $ F = q E $ |
und das zweite Newtonsche Gesetz in seiner allgemeinen Form (in Bezug auf den Impuls $p$ anstelle der Beschleunigung) wie folgt ausgedrückt wird:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
können wir schlussfolgern, dass die Bewegungsgleichung in einem ruhenden System wie folgt lautet:
| $ \displaystyle\frac{dp}{dt} = q E $ |
ID:(11791, 0)
Relative Masse
Gleichung
Im relativistischen Fall wird das elektrische Feld durch folgende Gleichung beschrieben:
| $ E_{d,v} = \gamma E_{d,0} $ |
in Verbindung mit der Bewegungsgleichung:
| $ \displaystyle\frac{dp}{dt} = q E $ |
und der Definition des Impulses:
| $ p = m_i v $ |
Dies impliziert, dass die Masse in Abhängigkeit von der Geschwindigkeit des Systems in folgender Weise variieren muss, um die Dynamik invariant unter relativistischen Transformationen zu halten:
| $ m_v = \gamma m_0 $ |
ID:(11792, 0)
Gedankenexperiment über Masse und Ladung
Bild
Ein 'Gedankenexperiment' kann durchgeführt werden, indem man sich eine Box mit zwei Ladungen vorstellt, die an einem drehbaren Arm befestigt sind. Die Relativitätstheorie impliziert, dass aufgrund der Bewegung ihre Masse zunehmen wird. Wenn wir diese Box an einem Dynamometer (einer Art Marktwaage) aufhängen, wird es sich ausdehnen und auf ein höheres Gewicht hinweisen. Der elektrische Feld gemessen außerhalb der Box wird sich jedoch nicht verändert haben:
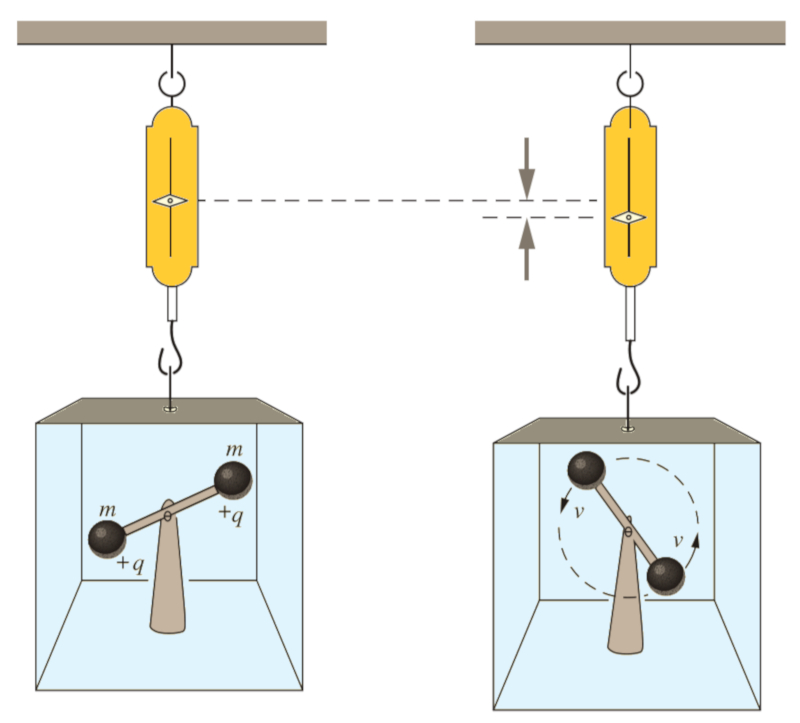
Das Konzept des 'Gedankenexperiments' wurde von Einstein eingeführt, um die Ableitung verschiedener Gesetze der speziellen Relativitätstheorie zu erleichtern.
ID:(11794, 0)