Potencial elétrico
Storyboard 
Sempre que o conceito de força é introduzido, e consequentemente o de energia, é possível modelar a força usando energia potencial. Da mesma forma, para a força descrita pela lei de Coulomb, pode-se derivar uma energia potencial, que neste contexto é conhecida como potencial elétrico.
ID:(1561, 0)
Potencial elétrico
Storyboard 
Sempre que o conceito de força é introduzido, e consequentemente o de energia, é possível modelar a força usando energia potencial. Da mesma forma, para a força descrita pela lei de Coulomb, pode-se derivar uma energia potencial, que neste contexto é conhecida como potencial elétrico.
Variáveis
Cálculos
Cálculos
Equações
La diferença potencial ($\Delta\varphi$) igual soma de o campo elétrico ($\vec{E}$) ao longo de um caminho integrado sobre o elemento do caminho percorrido ($d\vec{s}$):
Como la diferença potencial ($\Delta\varphi$) calculado considerando o potencial elétrico ($\varphi$) menos o potencial elétrico básico ($\varphi_0$):
portanto
Como la variação infinitesimal de trabalho ($dW$) est relacionado com la força ($\vec{F}$) e o elemento do caminho percorrido ($d\vec{s}$) por:
e a for a pode ser expressa em fun o de o campo elétrico ($\vec{E}$) e la carga de teste ($q$) como:
a energia associada ao campo el trico pode ser calculada usando:
La variação infinitesimal de potencial ($d\varphi$) La variação infinitesimal de trabalho ($dW$) multiplicado por la carga de teste ($q$):
Portanto, com o campo elétrico ($\vec{E}$) e o elemento do caminho percorrido ($d\vec{s}$):
Isso resulta em:
A unidade de medida para o potencial el trico Newton metro por Coulomb (N m/C ou J/C), que denominado Volt.
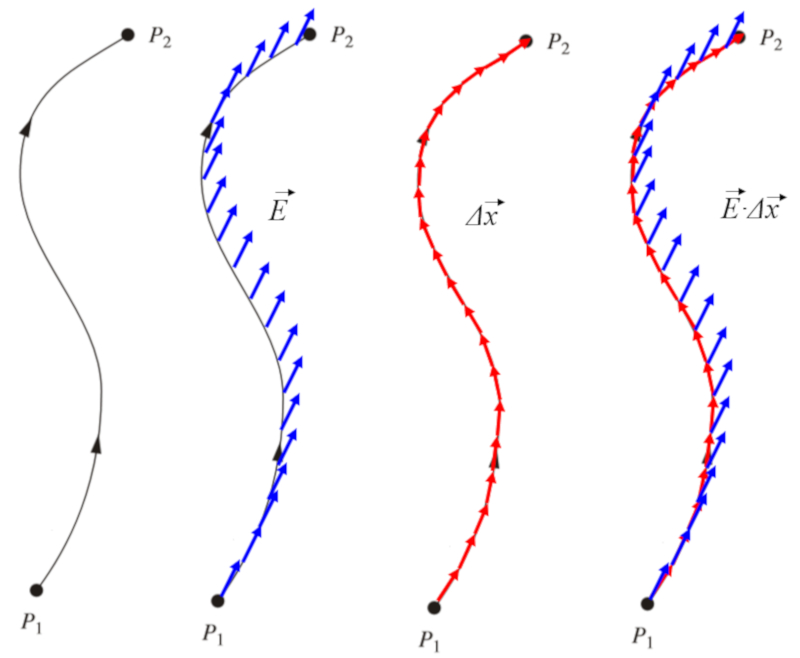
Se somarmos as contribui es de la variação infinitesimal de potencial ($d\varphi$) com o campo elétrico ($\vec{E}$) sobre um elemento do caminho percorrido ($d\vec{s}$):
obt m-se la diferença de potencial ($d\varphi$):
$d\varphi_1+d\varphi_2+d\varphi_3+\ldots = \displaystyle\sum_i d\varphi_i = \Delta\varphi$
e a soma dos campos ao longo dos caminhos:
$\vec{E}_1\cdot d\vec{s}_1+\vec{E}_2\cdot d\vec{s}_2+\vec{E}_3\cdot d\vec{s}_3+\ldots = \displaystyle\sum_i \vec{E}_i \cdot d\vec{s}_i$
que no limite cont nuo pode ser escrito como a integral de:
Ao calcular a integral de o campo elétrico ($E$) sobre um caminho fechado o elemento do caminho percorrido ($d\vec{s}$), ela pode ser decomposta em duas partes: uma de P1 para P2 e outra de volta de P2 para P1. Isso resulta em
$\displaystyle\oint_C \vec{E}\cdot d\vec{s} = \displaystyle\oint_{P1}^{P2} \vec{E}\cdot d\vec{s} - \displaystyle\oint_{P2}^{P1} \vec{E}\cdot d\vec{s} = 0$
portanto, com
Portanto,
Se uma part cula carregada percorre um caminho fechado em um campo el trico, o campo fornecer a mesma quantidade de energia que a part cula necessita para completar o caminho.
Como la variação infinitesimal de potencial ($d\varphi$) o produto de o campo elétrico ($\vec{E}$) com o elemento do caminho percorrido ($d\vec{s}$)
e considerando os componentes de o campo elétrico ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
junto com os de o elemento do caminho percorrido ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
a express o pode ser simplificada para
$d\varphi = -E_x dx - E_y dy - E_z dz$
Com a varia o do potencial
e o gradiente calculado como
conclui-se que o gradiente do potencial igual ao negativo do campo el trico.
Exemplos
Se m ltiplos valores de ERROR:5480,0 forem considerados ao longo de um caminho, poss vel calcular a energia por carga, correspondente a o potencial elétrico ($\varphi$), necess ria para mover uma carga ao longo desse caminho com uma for a por carga que corresponde a o campo elétrico ($\vec{E}$):
Isso representado graficamente como:
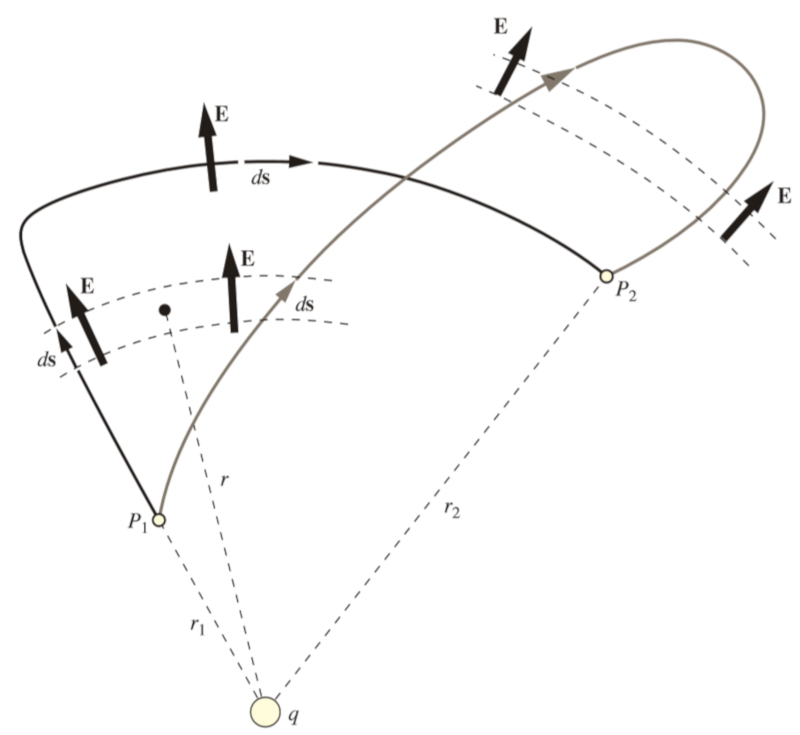
Se considerarmos dois caminhos distintos,
• um em que se chega a uma certa dist ncia da carga e depois se aproxima dela de forma perpendicular ao campo el trico,
• outro em que se afasta mais da origem e depois retorna carga, compensando a dist ncia adicional pelo sinal,
observar-se- que ambos os caminhos produzem o mesmo resultado:
Portanto, podemos concluir que
O potencial el trico entre dois pontos igual ao integral de linha do campo el trico ao longo de um segmento, sendo este integral independente do caminho escolhido.
Com esse conhecimento, poss vel proceder estimativa de campos el tricos escolhendo o caminho mais simples para a integra o ou soma de campos ao longo dos segmentos.
La variação infinitesimal de trabalho ($dW$) com o campo elétrico ($\vec{E}$), la carga de teste ($q$) e o elemento do caminho percorrido ($d\vec{s}$) igual a
No contexto da energia para uma carga la carga de teste ($q$), surge novamente o problema de um par metro que, ao ser medido, depende dos instrumentos de medi o. Portanto, faz sentido definir a energia por unidade de carga. Assim, la variação infinitesimal de potencial ($d\varphi$) introduzido como la variação infinitesimal de trabalho ($dW$) vezes la carga de teste ($q$):
Um sinal negativo inclu do porque se entende que esta a energia consumida, ou seja, subtra da do sistema.
La variação infinitesimal de potencial ($d\varphi$) com o campo elétrico ($\vec{E}$) e o elemento do caminho percorrido ($d\vec{s}$) o mesmo
La diferença potencial ($\Delta\varphi$) igual soma de o campo elétrico ($\vec{E}$) ao longo de um caminho integrado sobre o elemento do caminho percorrido ($d\vec{s}$):
La diferença potencial ($\Delta\varphi$) calculado considerando o potencial elétrico ($\varphi$) menos o potencial elétrico básico ($\varphi_0$):
O potencial elétrico ($\varphi$) pode ser calculado a partir de o potencial elétrico básico ($\varphi_0$) e o campo elétrico ($\vec{E}$) integrados ao longo de um caminho sobre o elemento do caminho percorrido ($d\vec{s}$):
A integral do produto de o campo elétrico ($E$) multiplicado na dire o do caminho, ou seja, integrado sobre o elemento do caminho percorrido ($d\vec{s}$) ao longo de um caminho fechado, zero:
O campo elétrico ($\vec{E}$) igual a menos que o gradiente de o potencial elétrico ($\varphi$):
ID:(1561, 0)