Elektrisches Potenzial
Storyboard 
Jedes Mal, wenn das Konzept der Kraft und damit das Konzept der Energie eingeführt wird, kann die Kraft unter Verwendung potenzieller Energie modelliert werden. Auf die gleiche Weise kann eine potentielle Energie für die durch das Coulombsche Gesetz definierte Kraft abgeleitet werden, die in diesem Fall als elektrisches Potential bezeichnet wird.
ID:(1561, 0)
Elektrisches Potenzial
Storyboard 
Jedes Mal, wenn das Konzept der Kraft und damit das Konzept der Energie eingeführt wird, kann die Kraft unter Verwendung potenzieller Energie modelliert werden. Auf die gleiche Weise kann eine potentielle Energie für die durch das Coulombsche Gesetz definierte Kraft abgeleitet werden, die in diesem Fall als elektrisches Potential bezeichnet wird.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Potentialdifferenz ($\Delta\varphi$) entspricht der Summe von der Elektrisches Feld ($\vec{E}$) entlang eines integrierten Pfades ber der Wegelement zurückgelegt ($d\vec{s}$):
Da die Potentialdifferenz ($\Delta\varphi$) berechnet wird, indem man der Elektrisches Potential ($\varphi$) minus der Elektrisches Grundpotential ($\varphi_0$) betrachtet:
deshalb
Da die Unendlich kleine Variation der Arbeit ($dW$) in Beziehung zu die Kraft ($\vec{F}$) und der Wegelement zurückgelegt ($d\vec{s}$) steht durch:
und die Kraft in Abh ngigkeit von der Elektrisches Feld ($\vec{E}$) und die Test Ladung ($q$) ausgedr ckt werden kann als:
kann die mit dem elektrischen Feld verbundene Energie berechnet werden mit:
Die Infinitesimale Variation des Potenzials ($d\varphi$) ist die Unendlich kleine Variation der Arbeit ($dW$) mal die Test Ladung ($q$):
Daher, mit der Elektrisches Feld ($\vec{E}$) und der Wegelement zurückgelegt ($d\vec{s}$):
Dies ergibt:
Die Einheit zur Messung des elektrischen Potentials ist Newtonmeter pro Coulomb (N m/C oder J/C), was als Volt bezeichnet wird.
Wenn die Beitr ge von die Infinitesimale Variation des Potenzials ($d\varphi$) mit der Elektrisches Feld ($\vec{E}$) ber ein Wegelement zurückgelegt ($d\vec{s}$) summiert werden:
erhalten wir die Potentialdifferenz ($d\varphi$):
$d\varphi_1+d\varphi_2+d\varphi_3+\ldots = \displaystyle\sum_i d\varphi_i = \Delta\varphi$
und die Summe der Felder entlang der Wege:
$\vec{E}_1\cdot d\vec{s}_1+\vec{E}_2\cdot d\vec{s}_2+\vec{E}_3\cdot d\vec{s}_3+\ldots = \displaystyle\sum_i \vec{E}_i \cdot d\vec{s}_i$
was im kontinuierlichen Grenzfall als das Integral von:
geschrieben werden kann.
Bei der Berechnung des Integrals von der Elektrisches Feld ($E$) ber einen geschlossenen Pfad der Wegelement zurückgelegt ($d\vec{s}$) kann das Integral in zwei Teile zerlegt werden: einen von P1 nach P2 und einen zur ck von P2 nach P1. Dadurch ergibt sich
$\displaystyle\oint_C \vec{E}\cdot d\vec{s} = \displaystyle\oint_{P1}^{P2} \vec{E}\cdot d\vec{s} - \displaystyle\oint_{P2}^{P1} \vec{E}\cdot d\vec{s} = 0$
daher, mit
Deshalb,
Wenn ein geladenes Teilchen einen geschlossenen Weg in einem elektrischen Feld zur cklegt, wird das Feld die gleiche Menge an Energie bereitstellen, wie sie vom Teilchen ben tigt wird, um den Weg zu vollenden.
Da die Infinitesimale Variation des Potenzials ($d\varphi$) das Produkt von der Elektrisches Feld ($\vec{E}$) und der Wegelement zurückgelegt ($d\vec{s}$) ist
und unter Ber cksichtigung der Komponenten von der Elektrisches Feld ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
zusammen mit denen von der Wegelement zurückgelegt ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
kann der Ausdruck vereinfacht werden zu
$d\varphi = -E_x dx - E_y dy - E_z dz$
Mit der Ver nderung des Potentials
und dem berechneten Gradienten
folgt, dass der Gradient des Potentials gleich dem negativen elektrischen Feld ist.
Beispiele
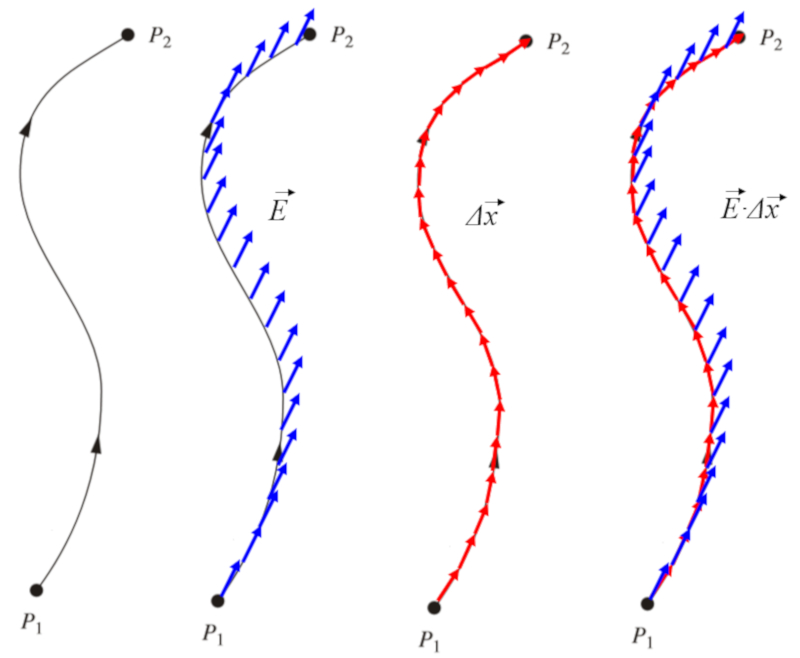
Wenn entlang eines Pfades mehrere Werte von ERROR:5480,0 betrachtet werden, l sst sich die Energie pro Ladung berechnen, die dem Wert der Elektrisches Potential ($\varphi$) entspricht. Diese Energie ist notwendig, um eine Ladung entlang dieses Weges mit einer Kraft pro Ladung, die der Elektrisches Feld ($\vec{E}$) entspricht, zu bewegen:
Dies wird grafisch wie folgt dargestellt:
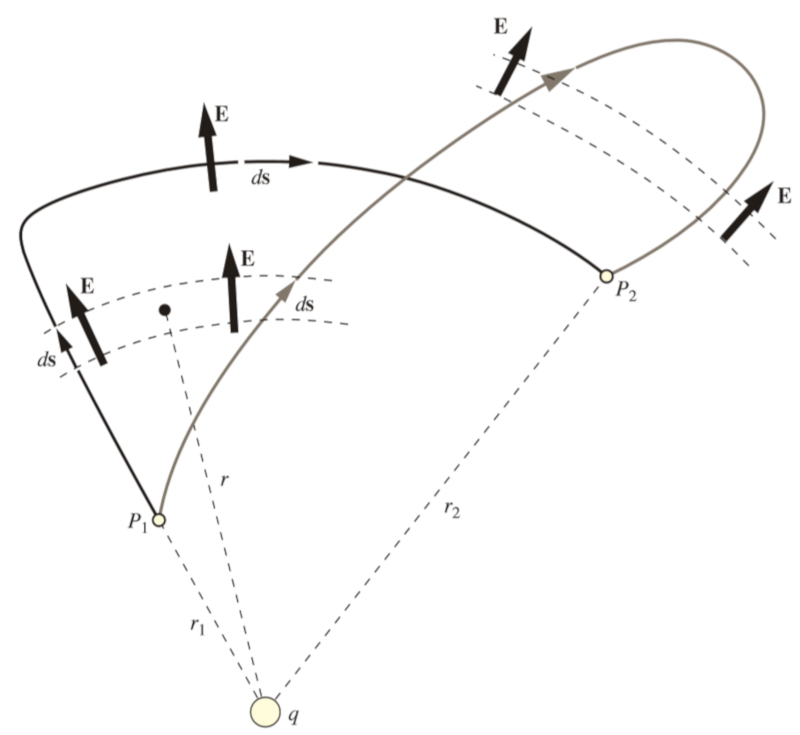
Wenn wir zwei verschiedene Wege betrachten,
• einen, bei dem man sich einer Ladung aus einer bestimmten Entfernung n hert und sich dann senkrecht zum elektrischen Feld auf sie zu bewegt,
• einen anderen, bei dem man sich weiter vom Ursprung entfernt und dann zur Ladung zur ckkehrt, wobei der zus tzliche Weg durch das Vorzeichen ausgeglichen wird,
wird beobachtet, dass beide Wege das gleiche Ergebnis liefern:
Daher k nnen wir folgern, dass
Das elektrische Potential zwischen zwei Punkten entspricht dem Linienintegral des elektrischen Feldes entlang eines Segments, wobei das Integral unabh ngig vom gew hlten Weg ist.
Mit diesem Wissen kann man weiterhin elektrische Felder absch tzen, indem man den einfachsten Weg f r die Integration oder Summation von Feldern entlang von Segmenten w hlt.
Die Unendlich kleine Variation der Arbeit ($dW$) ist mit der Elektrisches Feld ($\vec{E}$), die Test Ladung ($q$) und der Wegelement zurückgelegt ($d\vec{s}$) gleich
In Bezug auf die Energie f r eine Ladung die Test Ladung ($q$) tritt erneut das Problem auf, dass ein Parameter, der gemessen wird, von den Messinstrumenten abh ngt. Daher ist es sinnvoll, die Energie pro Ladungseinheit zu definieren. So wird die Infinitesimale Variation des Potenzials ($d\varphi$) als die Unendlich kleine Variation der Arbeit ($dW$) mal die Test Ladung ($q$) eingef hrt:
Ein negatives Vorzeichen wird hinzugef gt, da es sich um die Energie handelt, die verbraucht wird, also vom System abgezogen wird.
Die Infinitesimale Variation des Potenzials ($d\varphi$) ist mit der Elektrisches Feld ($\vec{E}$) und der Wegelement zurückgelegt ($d\vec{s}$) identisch
Die Potentialdifferenz ($\Delta\varphi$) entspricht der Summe von der Elektrisches Feld ($\vec{E}$) entlang eines ber der Wegelement zurückgelegt ($d\vec{s}$) integrierten Pfads:
Die Potentialdifferenz ($\Delta\varphi$) wird unter Ber cksichtigung von der Elektrisches Potential ($\varphi$) minus der Elektrisches Grundpotential ($\varphi_0$) berechnet:
Der Elektrisches Potential ($\varphi$) kann aus der Elektrisches Grundpotential ($\varphi_0$) und der Elektrisches Feld ($\vec{E}$) berechnet werden, die entlang eines Pfads ber der Wegelement zurückgelegt ($d\vec{s}$) integriert werden:
Das Integral des Produkts von der Elektrisches Feld ($E$) multipliziert in Richtung des Pfades, also integriert ber der Wegelement zurückgelegt ($d\vec{s}$) entlang eines geschlossenen Pfades, ist Null:
Der Elektrisches Feld ($\vec{E}$) ist gleich kleiner als der Gradient von der Elektrisches Potential ($\varphi$):
ID:(1561, 0)