Potentiel électrique
Storyboard 
Chaque fois que le concept de force est introduit, et par conséquent celui d'énergie, il est possible de modéliser la force à l'aide d'une énergie potentielle. De même, pour la force décrite par la loi de Coulomb, on peut dériver une énergie potentielle, qui dans ce contexte est appelée potentiel électrique.
ID:(1561, 0)
Potentiel électrique
Storyboard 
Chaque fois que le concept de force est introduit, et par conséquent celui d'énergie, il est possible de modéliser la force à l'aide d'une énergie potentielle. De même, pour la force décrite par la loi de Coulomb, on peut dériver une énergie potentielle, qui dans ce contexte est appelée potentiel électrique.
Variables
Calculs
Calculs
Équations
A différence potentielle ($\Delta\varphi$) est gal la somme de le champ électrique ($\vec{E}$) le long d'un chemin int gr sur le élément de chemin parcouru ($d\vec{s}$) :
Comme a différence potentielle ($\Delta\varphi$) est calcul en consid rant le potentiel électrique ($\varphi$) moins le potentiel électrique de base ($\varphi_0$) :
donc
tant donn que a variation infinitésimale du travail ($dW$) est li a force ($\vec{F}$) et le élément de chemin parcouru ($d\vec{s}$) par:
et que la force peut tre exprim e en fonction de le champ électrique ($\vec{E}$) et a charge d'essai ($q$) comme suit:
l' nergie associ e au champ lectrique peut tre calcul e en utilisant:
A variation infinitésimale du potentiel ($d\varphi$) est a variation infinitésimale du travail ($dW$) multipli par a charge d'essai ($q$) :
Donc, avec le champ électrique ($\vec{E}$) et le élément de chemin parcouru ($d\vec{s}$) :
Cela donne :
L'unit de mesure du potentiel lectrique est le newton-m tre par coulomb (N m/C ou J/C), que l'on appelle le volt.
Si l'on additionne les contributions de a variation infinitésimale du potentiel ($d\varphi$) avec le champ électrique ($\vec{E}$) sur un élément de chemin parcouru ($d\vec{s}$) :
on obtient a différence de potentiel ($d\varphi$) :
$d\varphi_1+d\varphi_2+d\varphi_3+\ldots = \displaystyle\sum_i d\varphi_i = \Delta\varphi$
et la somme des champs le long des chemins :
$\vec{E}_1\cdot d\vec{s}_1+\vec{E}_2\cdot d\vec{s}_2+\vec{E}_3\cdot d\vec{s}_3+\ldots = \displaystyle\sum_i \vec{E}_i \cdot d\vec{s}_i$
qui, dans la limite continue, peut tre crite comme l'int grale de :
Lors du calcul de l'int grale de le champ électrique ($E$) sur un chemin ferm le élément de chemin parcouru ($d\vec{s}$), celle-ci peut tre d compos e en deux parties : une de P1 P2 et une autre de P2 P1. Cela donne
$\displaystyle\oint_C \vec{E}\cdot d\vec{s} = \displaystyle\oint_{P1}^{P2} \vec{E}\cdot d\vec{s} - \displaystyle\oint_{P2}^{P1} \vec{E}\cdot d\vec{s} = 0$
donc, avec
Par cons quent,
Si une particule charg e parcourt un chemin ferm dans un champ lectrique, le champ fournira la m me quantit d' nergie que celle requise par la particule pour compl ter le chemin.
Puisque a variation infinitésimale du potentiel ($d\varphi$) est le produit de le champ électrique ($\vec{E}$) et le élément de chemin parcouru ($d\vec{s}$)
et en consid rant les composantes de le champ électrique ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
ainsi que celles de le élément de chemin parcouru ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
l'expression peut tre simplifi e
$d\varphi = -E_x dx - E_y dy - E_z dz$
Avec la variation du potentiel
et le gradient calcul comme
il est conclu que le gradient du potentiel est gal au n gatif du champ lectrique.
Exemples
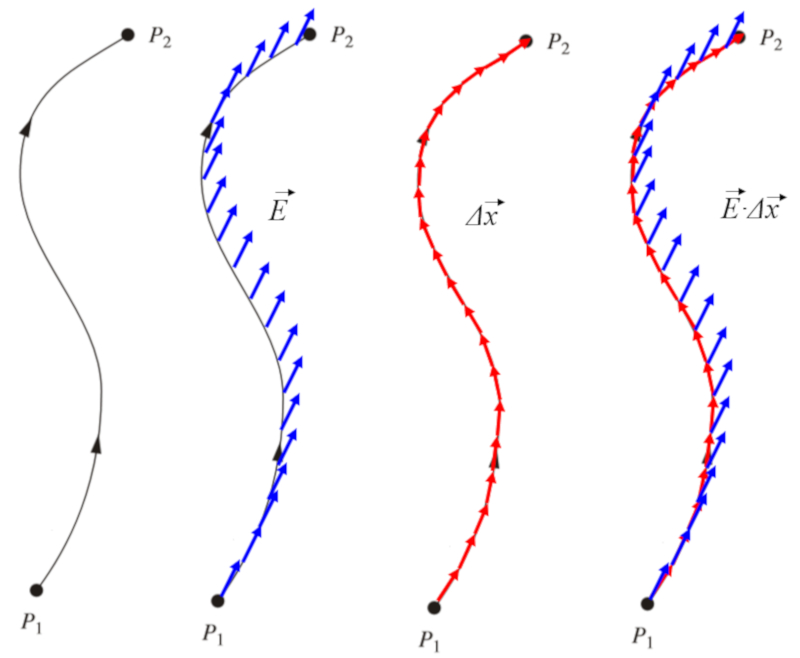
Si plusieurs valeurs de ERROR:5480,0 sont prises en compte le long d'un chemin, il est possible de calculer l' nergie par charge, correspondant le potentiel électrique ($\varphi$), n cessaire pour d placer une charge le long de ce chemin avec une force par charge correspondant le champ électrique ($\vec{E}$) :
Ceci est repr sent graphiquement comme suit :
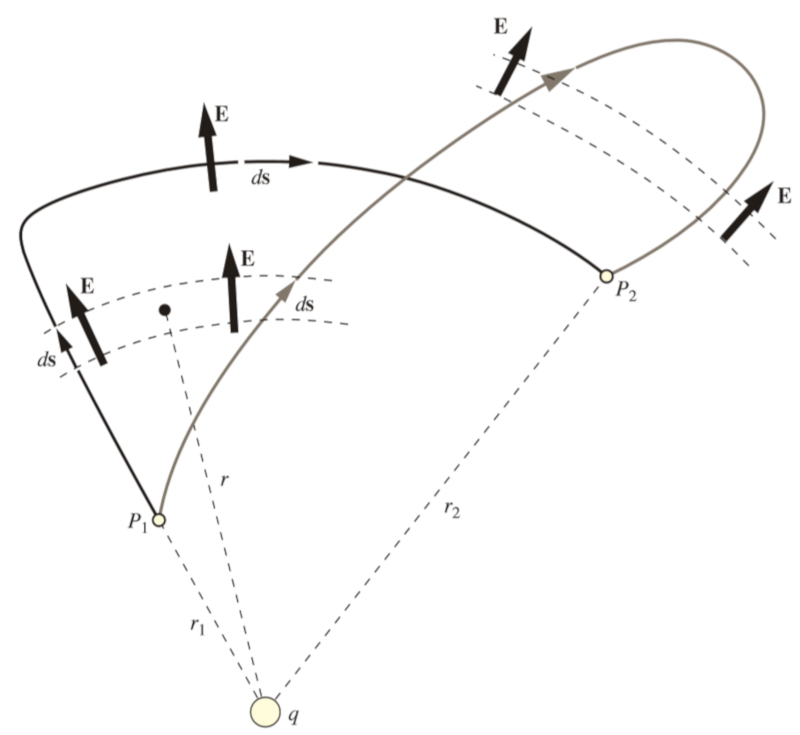
Si nous consid rons deux chemins diff rents,
• un o l'on s'approche d'une charge partir d'une certaine distance puis on se dirige vers elle perpendiculairement au champ lectrique,
• un autre o l'on s' loigne davantage de l'origine puis on revient vers la charge, compensant la distance suppl mentaire par le signe,
il sera observ que les deux chemins donnent le m me r sultat :
Par cons quent, nous pouvons conclure que
Le potentiel lectrique entre deux points est gal l'int grale curviligne du champ lectrique le long d'un segment, cette int grale tant ind pendante du chemin choisi.
Avec cette connaissance, on peut proc der l'estimation des champs lectriques en choisissant le chemin le plus simple pour l'int gration ou la sommation des champs le long des segments.
A variation infinitésimale du travail ($dW$) est avec le champ électrique ($\vec{E}$), a charge d'essai ($q$) et le élément de chemin parcouru ($d\vec{s}$) est gal
Dans le contexte de l' nergie pour une charge a charge d'essai ($q$), le probl me se pose nouveau d'un param tre qui, lorsqu'il est mesur , d pend des instruments de mesure. Par cons quent, il est logique de d finir l' nergie par unit de charge. Ainsi, a variation infinitésimale du potentiel ($d\varphi$) est introduit comme a variation infinitésimale du travail ($dW$) multipli par a charge d'essai ($q$) :
Un signe n gatif est inclus car on consid re qu'il s'agit de l' nergie consomm e, c'est- -dire soustraite du syst me.
A variation infinitésimale du potentiel ($d\varphi$) est identique le champ électrique ($\vec{E}$) et le élément de chemin parcouru ($d\vec{s}$)
A différence potentielle ($\Delta\varphi$) est gal la somme de le champ électrique ($\vec{E}$) le long d'un chemin int gr sur le élément de chemin parcouru ($d\vec{s}$)xa0:
A différence potentielle ($\Delta\varphi$) est calcul en consid rant le potentiel électrique ($\varphi$) moins le potentiel électrique de base ($\varphi_0$)xa0:
Le potentiel électrique ($\varphi$) peut tre calcul partir de le potentiel électrique de base ($\varphi_0$) et le champ électrique ($\vec{E}$) int gr s le long d'un chemin sur le élément de chemin parcouru ($d\vec{s}$)xa0:
L'int grale du produit de le champ électrique ($E$) multipli dans la direction du chemin, c'est- -dire int gr sur le élément de chemin parcouru ($d\vec{s}$) le long d'un chemin ferm , est nullexa0:
Le champ électrique ($\vec{E}$) est gal moins que le gradient de le potentiel électrique ($\varphi$)xa0:
ID:(1561, 0)