Electric potential
Storyboard 
Whenever the concept of force is introduced, and consequently that of energy, it is possible to model the force using potential energy. Similarly, for the force described by Coulomb's law, a potential energy can be derived, which in this context is known as electric potential.
ID:(1561, 0)
Electric potential
Storyboard 
Whenever the concept of force is introduced, and consequently that of energy, it is possible to model the force using potential energy. Similarly, for the force described by Coulomb's law, a potential energy can be derived, which in this context is known as electric potential.
Variables
Calculations
Calculations
Equations
The potential difference ($\Delta\varphi$) is equal to the sum of the electric field ($\vec{E}$) along an integrated path over the path element traveled ($d\vec{s}$):
As the potential difference ($\Delta\varphi$) is calculated by considering the electric potential ($\varphi$) minus the base electrical potential ($\varphi_0$):
therefore
Since the infinitesimal variation of work ($dW$) is related to the force ($\vec{F}$) and the path element traveled ($d\vec{s}$) by:
and the force can be expressed as a function of the electric field ($\vec{E}$) and the test charge ($q$) as:
the energy associated with the electric field can be calculated using:
The infinitesimal variation of potential ($d\varphi$) is the infinitesimal variation of work ($dW$) times the test charge ($q$):
Therefore, with the electric field ($\vec{E}$) and the path element traveled ($d\vec{s}$):
This results in:
The unit of measurement for electric potential is Newton meter per Coulomb (N m/C or J/C), commonly referred to as the Volt.
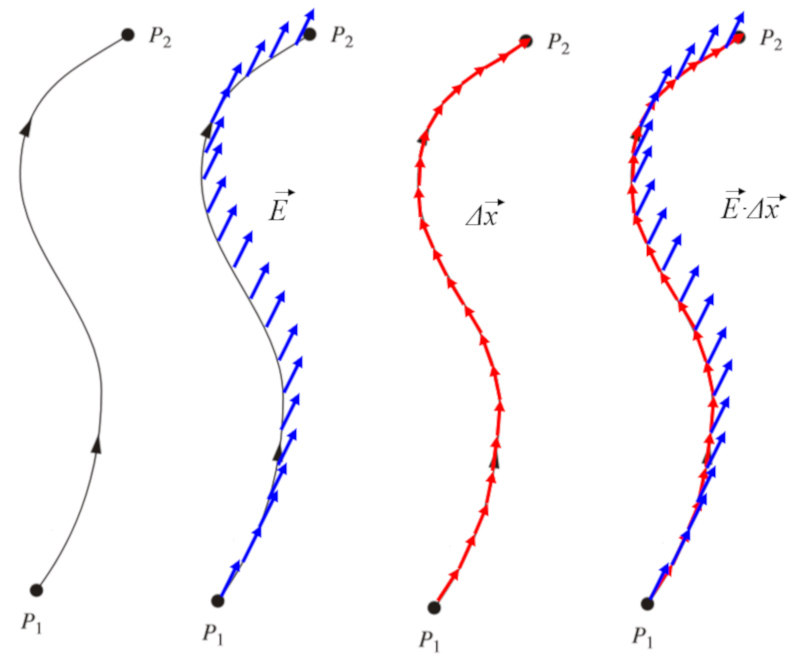
If the contributions of the infinitesimal variation of potential ($d\varphi$) with the electric field ($\vec{E}$) over a path element traveled ($d\vec{s}$) are summed:
we get the potential difference ($d\varphi$):
$d\varphi_1+d\varphi_2+d\varphi_3+\ldots = \displaystyle\sum_i d\varphi_i = \Delta\varphi$
and the sum of the fields along paths:
$\vec{E}_1\cdot d\vec{s}_1+\vec{E}_2\cdot d\vec{s}_2+\vec{E}_3\cdot d\vec{s}_3+\ldots = \displaystyle\sum_i \vec{E}_i \cdot d\vec{s}_i$
which in the continuous limit can be written as the integral of:
When calculating the integral of the electric eield ($E$) over a closed path the path element traveled ($d\vec{s}$), it can be decomposed into two parts: one from P1 to P2 and another back from P2 to P1. This gives us
$\displaystyle\oint_C \vec{E}\cdot d\vec{s} = \displaystyle\oint_{P1}^{P2} \vec{E}\cdot d\vec{s} - \displaystyle\oint_{P2}^{P1} \vec{E}\cdot d\vec{s} = 0$
therefore, with
Therefore,
If a charged particle travels a closed path in an electric field, the field will provide the same amount of energy as it requires from the particle to complete the path.
Since the infinitesimal variation of potential ($d\varphi$) is the product of the electric field ($\vec{E}$) and the path element traveled ($d\vec{s}$)
and considering the components of the electric field ($\vec{E}$)
$\vec{E} = \hat{x} E_x + \hat{y} E_y + \hat{z} E_z$
along with those of the path element traveled ($d\vec{s}$)
$d\vec{s} = \hat{x} dx + \hat{y} dy + \hat{z} dz$
the expression can be simplified to
$d\varphi = -E_x dx - E_y dy - E_z dz$
With the variation of potential
and the gradient calculated as
it is concluded that the gradient of the potential is equal to the negative of the electric field.
Examples
If multiple values of ERROR:5480,0 are considered along a path, it is possible to calculate the energy per charge, corresponding to the electric potential ($\varphi$), needed to move a charge along this path with a force per charge that corresponds to the electric field ($\vec{E}$):
This is represented graphically as:
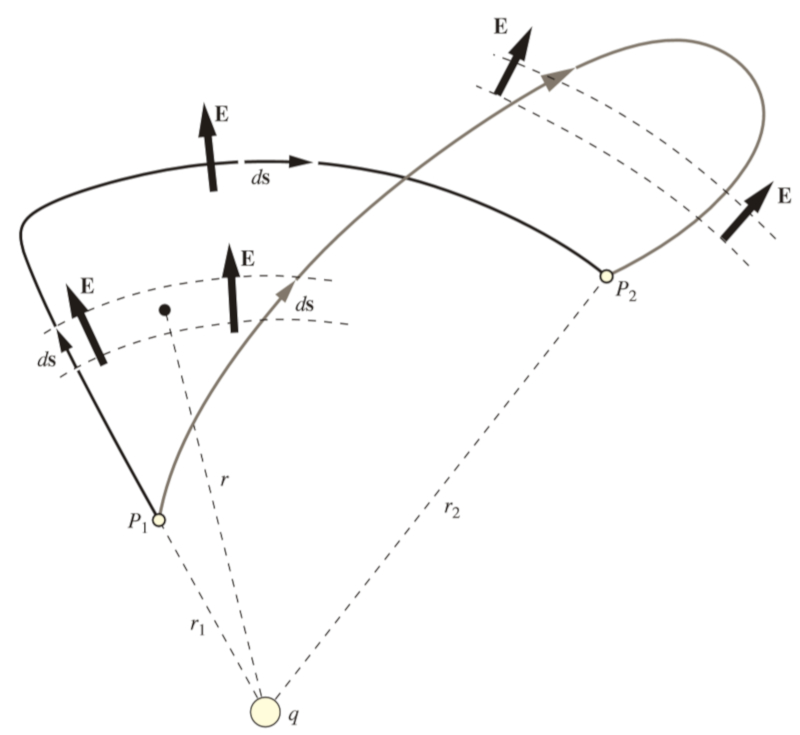
If we consider two different paths,
• one in which you approach a charge from a distance and then move toward it perpendicular to the electric field,
• another in which you move further away from the origin and then return to the charge, offsetting the extra distance by the sign,
it will be observed that both paths yield the same result:
Therefore, we can conclude that
The electric potential between two points is equal to the line integral of the electric field along a segment, with the integral being independent of the chosen path.
With this knowledge, one can proceed to estimate electric fields by choosing the simplest path for the integration or summation of fields along segments.
The infinitesimal variation of work ($dW$) is with the electric field ($\vec{E}$), the test charge ($q$) and the path element traveled ($d\vec{s}$) is equal to
In the context of energy for a charge the test charge ($q$), the issue arises again of a parameter that, when measured, depends on the measurement instruments. Therefore, it makes sense to define energy per unit charge. Thus, the infinitesimal variation of potential ($d\varphi$) is introduced as the infinitesimal variation of work ($dW$) times the test charge ($q$):
A negative sign is included because it is understood that this is the energy being consumed, i.e., subtracted from the system.
The infinitesimal variation of potential ($d\varphi$) is with the electric field ($\vec{E}$) and the path element traveled ($d\vec{s}$) the same
The potential difference ($\Delta\varphi$) is equal to the sum of the electric field ($\vec{E}$) along a path integrated over the path element traveled ($d\vec{s}$):
The potential difference ($\Delta\varphi$) is calculated considering the electric potential ($\varphi$) minus the base electrical potential ($\varphi_0$):
The electric potential ($\varphi$) can be calculated from the base electrical potential ($\varphi_0$) and the electric field ($\vec{E}$) integrated along a path over the path element traveled ($d\vec{s}$):
The integral of the product of the electric eield ($E$) multiplied in the direction of the path, that is, integrated over the path element traveled ($d\vec{s}$) along a closed path, is zero:
The electric field ($\vec{E}$) is equal to less than the gradient of the electric potential ($\varphi$):
ID:(1561, 0)