Usuario:
Circuitos RC
Descripción 
Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$C$
C
Capacidad del condensador
F
$I$
I
Corriente
A
$\Delta\varphi_C$
Dphi_C
Diferencia de potencial en la capacitancia
V
$\Delta V$
DV
Diferencia de potencial en la fuente
V
$R$
R
Resistencia
Ohm
$t$
t
Tiempo
s
Cálculos
Primero, seleccione la ecuación: 
a 
,
luego, seleccione la variable: 
a 
a ,
luego, seleccione la variable:
a
Símbolo
Ecuación
Resuelto
Traducido
Cálculos
Símbolo
Ecuación
Resuelto
Traducido
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
El circuito RC es un circuito con una capacitancia y una resistencia tal como se ve en esta iamagen:
(ID 12071)
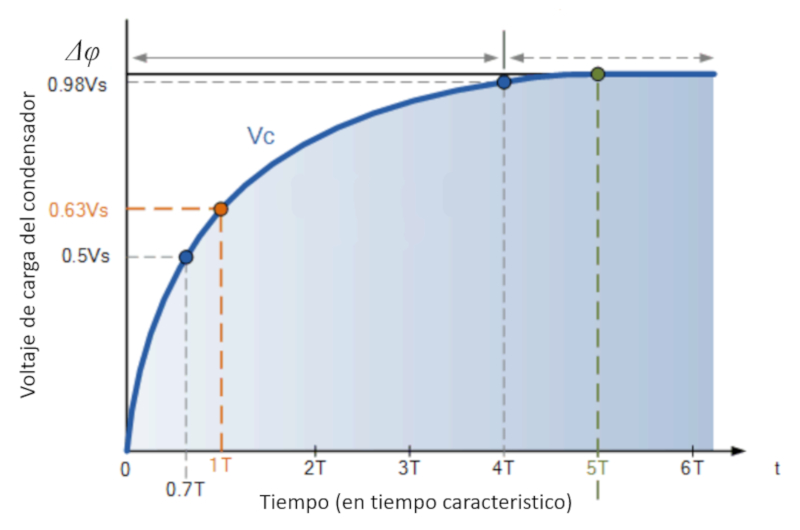
Cuando se conecta la bater a al circuito se puede cargar el condensador:
(ID 12072)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12073)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12075)
Cuando se cierra el circuito se puede descargar el condensador:
(ID 12074)
ID:(1622, 0)