Usuario:


Elementos LC
Storyboard

>Modelo

ID:(1636, 0)


Resistencia de una inductancia
Definición

ID:(12270, 0)


Elementos LC
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$C$
C
Capacitancia
F
$I_C$
I_C
Corriente por la capacitancia
A
$I_L$
I_L
Corriente por la inductancia
A
$I_p$
I_p
Corriente por LC en paralelo
A
$I_s$
I_s
Corriente por LC en serie
A
$\Delta\varphi_p$
Dphi_p
Diferencia de potencial de L y C en paralelo
V
$\Delta\varphi_s$
Dphi_s
Diferencia de potencial de L y C en serie
V
$\Delta\varphi_C$
Dphi_C
Diferencia de potencial en la capacitancia
V
$\Delta\varphi_L$
Dphi_L
Diferencia de potencial en la inductancia
V
$\omega$
omega
Frecuencia angular de la corriente alterna
rad/s
$L$
L
Inductancia
kg m^2/C^2
$X_p$
X_p
Resistencia de L y C en paralelo
Ohm
$X_s$
X_s
Resistencia de L y C en serie
Ohm
$X_C$
X_C
Resistencia de la capacitancia
Ohm
$X_L$
X_L
Resistencia de la inductancia
Ohm

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Una inductancia genera seg n la ley de Lenz un campo que se opone a la corriente que circula por ella lo que se observa como una resistencia. El diagrama para una inductancia conectada a una diferencia de de potencial se muestra a continuaci n:

(ID 12270)

Bajo la corriente alterna una capacitancia es peri dicamente polarizada y despolarizada existiendo tambi n una resistencia a dicha situaci n. En este caso se tiene que la capacitancia conectada se describe con el siguiente diagrama:

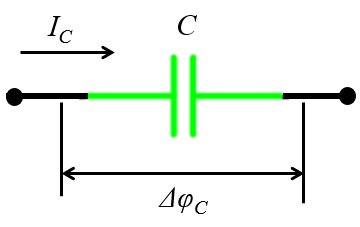
(ID 12271)

Si se conecta una inductancia y capacitancia en serie con los respectivas ca das de potenciales lo que se muestra en el siguiente diagrama:

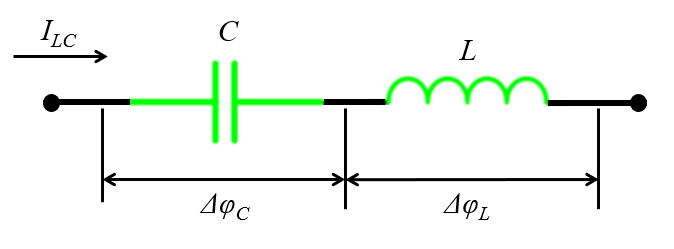
(ID 12272)

Si se conecta una inductancia y capacitancia en paralelo con los respectivas ca das de potenciales lo que se muestra en el siguiente diagrama:

(ID 12273)

ID:(1636, 0)