User:
R-LC elements and resonance
Description 
Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\omega$
omega
Angular frequency of alternating current
rad/s
$Z_p$
Z_p
Apparent resistance of L and C in parallel
Ohm
$Z_s$
Z_s
Apparent resistance of L and C in series
Ohm
$C$
C
Capacitance
F
$I_{Rp}$
I_Rp
Current through R in LC series
A
$I_{Rs}$
I_Rs
Current through R in parallel LC
A
$I_R$
I_R
Current through resistance
A
$I_X$
I_X
Current times apparent resistance
A
$L$
L
Inductance
kg m^2/C^2
$\phi$
phi
Phase shift
rad
$\Delta\varphi_{Rp}$
Dphi_Rp
Potential difference across R with L and C in parallel
V
$\Delta\varphi_{Rs}$
Dphi_Rs
Potential difference across R with L and C in series
V
$\Delta\varphi_X$
Dphi_X
Potential difference in apparent resistance
V
$\Delta\varphi_R$
Dphi_R
Potential difference in resistance
V
$X$
X
Reactance
Ohm
$R$
R
Resistance
Ohm
Calculations
First, select the equation: 
to 
,
then, select the variable: 
to 
to ,
then, select the variable:
to
Symbol
Equation
Solved
Translated
Calculations
Symbol
Equation
Solved
Translated
Variable
Given
Calculate
Target :
Equation
To be used
Equations
None
(ID 12293)
Examples
Si se conecta una resistencia en serie con una inductancia y capacitancia que est n conectadas en paralelo se tiene el siguiente diagrama:
(ID 12288)
Si se conecta una resistencia en paralelo con una inductancia y capacitancia que est n conectadas en paralelo se tiene el siguiente diagrama:
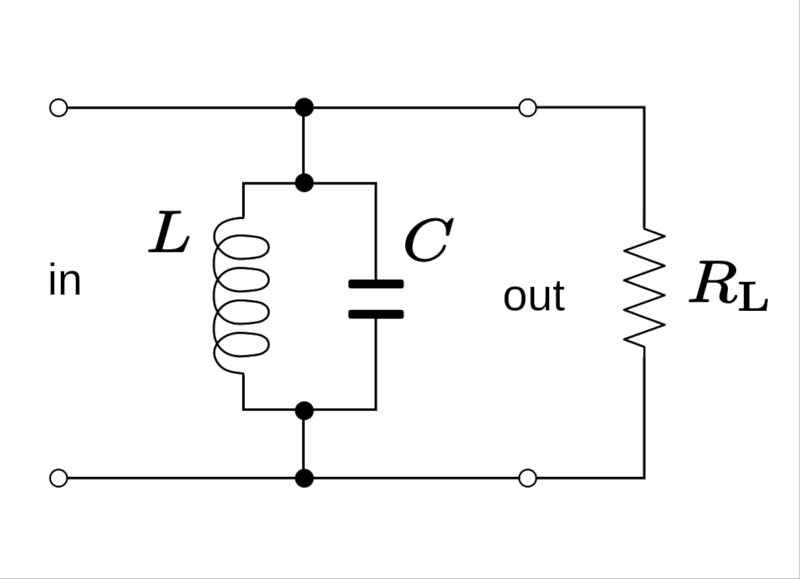
(ID 12289)
ID:(1637, 0)