Benützer:


R-LC-Elemente und Resonanz
Storyboard

>Modell

ID:(1637, 0)


R-LC-Elemente und Resonanz
Beschreibung

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$L$
L
Induktivität
kg m^2/C^2
$C$
C
Kapazität
F
$\phi$
phi
Phasenverschiebung
rad
$\Delta\varphi_{Rs}$
Dphi_Rs
Potentialdifferenz über R mit L und C in Reihe
V
$\Delta\varphi_{Rp}$
Dphi_Rp
Potentialdifferenz über R mit L und C parallel
V
$\Delta\varphi_X$
Dphi_X
Potenzieller Unterschied im scheinbaren Widerstand
V
$\Delta\varphi_R$
Dphi_R
Potenzieller Widerstandsunterschied
V
$X$
X
Reaktanz
Ohm
$Z_s$
Z_s
Scheinbarer Widerstand von L und C in Reihe
Ohm
$Z_p$
Z_p
Scheinbarer Widerstand von L und C parallel
Ohm
$I_X$
I_X
Strom durch den Scheinwiderstand
A
$I_{Rs}$
I_Rs
Strom durch R im Parallel-LC
A
$I_{Rp}$
I_Rp
Strom durch R in der LC-Reihe
A
$I_R$
I_R
Strom durch Widerstand
A
$R$
R
Widerstand
Ohm
$\omega$
omega
Winkelfrequenz von Wechselstrom
rad/s

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Si se conecta una resistencia en serie con una inductancia y capacitancia que est n conectadas en paralelo se tiene el siguiente diagrama:

(ID 12288)

Si se conecta una resistencia en paralelo con una inductancia y capacitancia que est n conectadas en paralelo se tiene el siguiente diagrama:

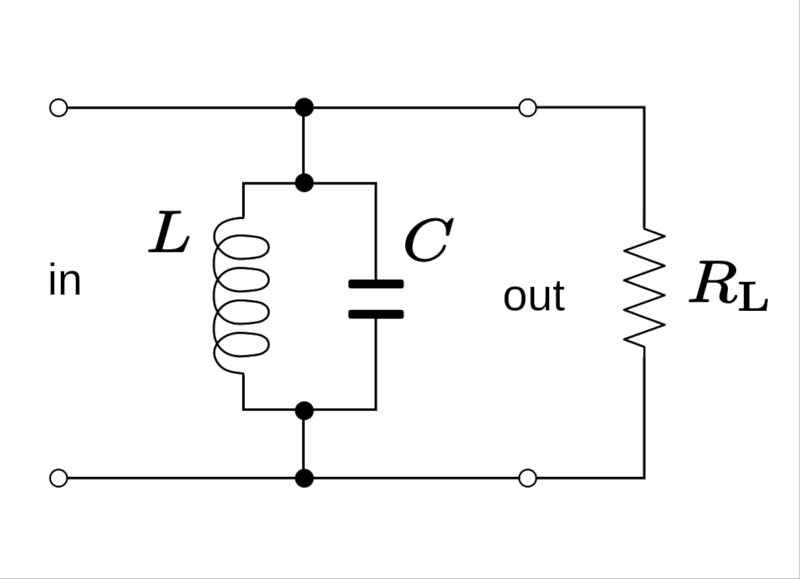
(ID 12289)

ID:(1637, 0)