Modelo de primavera sob forças
Storyboard 
No limite de pequenas deformações, onde as forças entre os átomos do sólido são proporcionais à distância do ponto de equilíbrio, o sólido pode ser modelado como uma série de massas interconectadas por molas.
ID:(1884, 0)
Modelo de primavera sob forças
Storyboard 
No limite de pequenas deformações, onde as forças entre os átomos do sólido são proporcionais à distância do ponto de equilíbrio, o sólido pode ser modelado como uma série de massas interconectadas por molas.
Variáveis
Cálculos
Cálculos
Equações
Como a la constante total de gancho de molas em paralelo ($k_p$) de la constante de Hook de mola i ($k_i$)
segue-se que, no caso de la microscopia constante de Hook ($k_m$) ser igual a
$k_p = N_p k_m$
la constante total de gancho de molas em paralelo ($k_p$) corresponde, neste caso, constante de Hook de uma se o de espessura monoat mica. Para obter a constante para o corpo inteiro, necess rio somar todas as se es em s rie, e para isso, trabalhamos com a rela o para a soma de la constante total de gancho de molas em série ($k_s$), dada por
Com o n mero de se es sendo igual a o número de molas em série ($N_s$), e se assumirmos que todas s o iguais, obtemos
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
ou seja,
$k = \displaystyle\frac{N_p}{N_s}k_m$
Por fim, com as rela es para o comprimento do corpo ($L$) e o comprimento microscópico da mola ($l$)
e com la seção de elemento ($S$) e la seção microscópica da mola ($s$)
obtemos finalmente
Quando aplicamos for as la força ($F$) nas extremidades das molas, as molas se alongar o (ou comprimir o) em la alongamento de mola i ($u_i$) e la constante de Hook de mola i ($k_i$) respectivamente. Se o ponto de contato entre ambas as molas estiver em repouso, a soma das for as que atuam sobre ele deve ser igual a zero, ou seja, elas devem ser iguais a la força ($F$). Portanto, para cada mola $i$, deve ser satisfeita a seguinte rela o:
$F = k_iu_i$
A elonga o total ser igual soma das elonga es individuais:
$u = \displaystyle\sum_iu_i$
E usando a lei de Hooke, isso pode ser expresso como:
$u = \displaystyle\sum_i\frac{F}{k_i}$
Se introduzirmos uma constante total para o caso de conex o em s rie la constante total de gancho de molas em série ($k_s$), tal que
$F = k_su$
Ent o, teremos:
Com a Lei de Hooke para la força elástica ($F_k$), la constante de Hooke ($k$) e la alongamento ($u$) da seguinte forma:
e a express o para la constante de Hooke ($k$) em termos de o comprimento do corpo ($L$), la seção de elemento ($S$), o comprimento microscópico da mola ($l$), la seção microscópica da mola ($s$) e la microscopia constante de Hook ($k_m$):
juntamente com a express o para o módulo de Elasticidade ($E$):
o resultado :
Uma vez que cada mola est exposta mesma for a aplicada la força ($F$), as molas com constantes la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) se deformar o em magnitudes la alongamento de mola 1 ($u_1$) e la alongamento de mola 2 ($u_2$), respectivamente, de acordo com as seguintes equa es:
$F = k_1u_1$
$F = k_2u_2$
A elonga o total ser a soma das duas elonga es:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Portanto, o sistema se comporta como se tivesse uma constante de mola igual a:
Uma vez que cada mola pode ter uma constante el stica diferente, representada por la constante de Hook de mola i ($k_i$), a for a contribu da por cada mola tamb m varia. De acordo com a lei de Hooke, as for as $F_i$ podem ser expressas como:
$F_i = k_i u$
Como a for a total $F$ corresponde soma das for as individuais, temos:
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
Portanto, uma constante el stica total pode ser definida como:
Dado que cada mola est sujeita mesma ERROR:5343,0, as for as ser o diferentes se as constantes da mola forem diferentes. Portanto, se la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) forem as constantes da mola, as for as ser o as seguintes:
$F_1 = k_1 u$
$F_2 = k_2 u$
Como resultado, a for a total ser :
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Assim, o sistema se comporta como se tivesse uma constante de mola igual a:
Exemplos
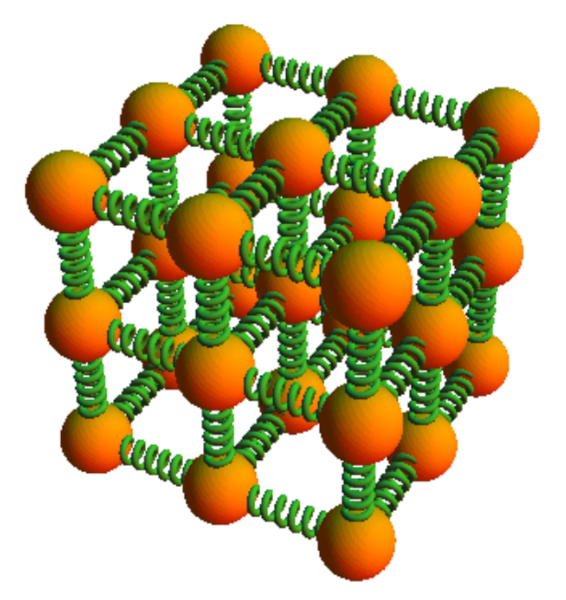
A intera o entre os tomos que comp em um s lido tal que cada tomo se encontra em equil brio, o que significa que a soma de todas as for as de seus vizinhos sobre ele nula. Quando um tomo deslocado de sua posi o de equil brio, essa soma deixa de ser nula. Em uma primeira aproxima o, pode-se assumir que, para pequenos deslocamentos, a for a proporcional dist ncia a partir da posi o de equil brio. Al m disso, a for a que depende da dist ncia percorrida se assemelha de uma mola. Em outras palavras, os tomos em um s lido se comportam como se estivessem conectados por molas quando sujeitos a pequenas deforma es:
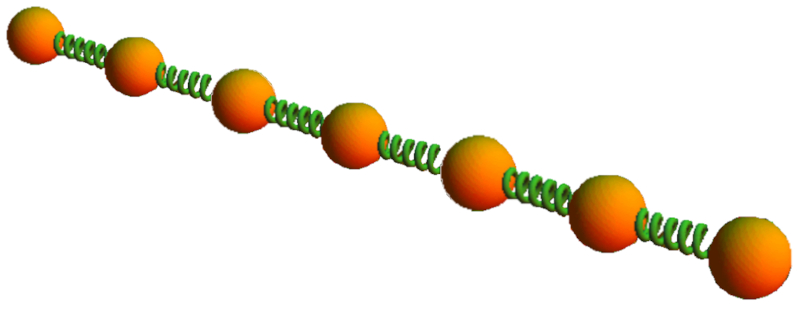
Se voc deseja modelar como um s lido se deforma sob a influ ncia de uma for a, pode primeiro considerar o comportamento de uma subunidade, como duas molas conectadas uma atr s da outra, conforme mostrado na imagem:
Esse tipo de arranjo das molas chamado de em s rie. Ele se caracteriza pelo fato de que a for a la força ($F$) a mesma em ambas as molas, e elas se deformam de acordo com la constante de Hooke ($k$). Portanto, a constante el stica equivalente la alongamento ($u$) calculada como a soma de la alongamento de mola 1 ($u_1$) e la alongamento de mola 2 ($u_2$), que, por sua vez, de acordo com a lei de Hooke:
igual a la força ($F$) dividido pelas constantes la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$), respectivamente:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Portanto, o sistema de duas molas pode ser tratado como uma nica mola cuja constante el stica equivalente la constante total de gancho de molas em série ($k_s$) calculada da seguinte forma:
No caso de dois molas com constantes la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$), que podem ser modeladas por uma nica mola com uma constante la constante total de gancho de molas em série ($k_s$) calculada usando a seguinte equa o:
Para o caso mais geral de molas com constantes ERROR:10228,0, a equa o pode ser generalizada da seguinte forma:
Isso nos permite modelar uma estrutura macro da seguinte maneira:
Se deseja modelar como um s lido se deforma sob a influ ncia de uma for a, primeiro poss vel considerar o comportamento de uma subunidade, como dois molas conectadas lado a lado, conforme mostrado na imagem:
Esse tipo de disposi o das molas chamado de em paralelo. caracterizado porque la alongamento ($u$) em ambas as molas o mesmo e cada mola contribui com ERROR:4975,0 em fun o de la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) de acordo com a lei de Hooke:
Portanto, temos que:
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Assim, o sistema de duas molas pode ser tratado como uma nica mola cuja constante el stica equivalente la constante total de gancho de molas em paralelo ($k_p$) calculada da seguinte forma:
No caso de dois molas com constantes la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) que podem ser modelados por uma nica mola com uma constante la constante total de gancho de molas em paralelo ($k_p$) calculada mediante a seguinte equa o:
Para o caso mais geral de molas com constantes ERROR:10228,0, a equa o pode ser generalizada da seguinte forma:
Isso nos permite modelar uma estrutura macro da seguinte forma:
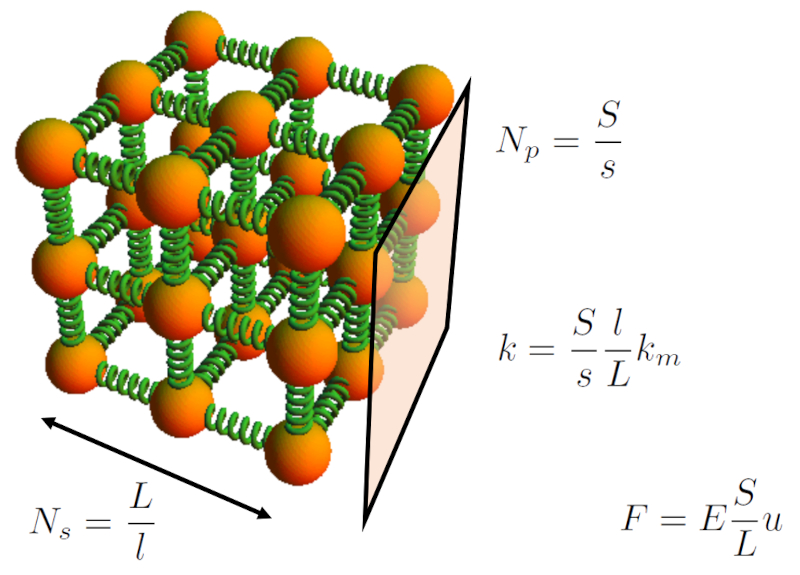
O s lido modelado como uma rede de molas cuja quantidade estimada com base em o comprimento do corpo ($L$) e la seção de elemento ($S$) em rela o a o comprimento microscópico da mola ($l$) e la seção microscópica da mola ($s$).
De acordo com essa estrutura, as molas de la microscopia constante de Hook ($k_m$) s o inicialmente somadas em paralelo sobre la seção de elemento ($S$), seguidas pela soma em s rie ao longo de ERROR:5355,0.
O resultado ent o inserido na lei de Hooke para la força elástica ($F_k$), la constante de Hooke ($k$) e la força elástica ($F_k$) usando a equa o:
resultando na equa o para a deforma o longitudinal de um s lido no limite el stico:
Se tivermos dois resistores com valores la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) conectados em s rie, as extens es se somam, fazendo com que cada resistor individual atue com base em seu inverso. Dessa forma, o inverso de la constante total de gancho de molas em série ($k_s$) igual soma dos inversos das constantes individuais la constante de Hook de mola i ($k_i$):
No caso de dois resistores com valores la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$), quando est o conectados em paralelo, eles agem como se houvesse uma resist ncia equivalente la constante total de gancho de molas em série ($k_s$) dada pela seguinte equa o:
Esse conceito pode ser generalizado para la constante de Hook de mola i ($k_i$) da seguinte forma:
Se voc tiver dois resistores com valores la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$) conectados em paralelo, seus efeitos se somam, agindo como se houvesse uma resist ncia equivalente la constante total de gancho de molas em paralelo ($k_p$) igual soma das constantes individuais:
No caso de dois resistores com valores la constante de Hook de mola 1 ($k_1$) e la constante de Hook de mola 2 ($k_2$), quando est o conectados em paralelo, eles se comportam como se houvesse uma resist ncia equivalente la constante total de gancho de molas em paralelo ($k_p$) dada pela seguinte equa o:
Esse conceito pode ser generalizado para la constante de Hook de mola i ($k_i$) da seguinte forma:
Para calcular o equivalente macrosc pico da constante da mola microsc pica, necess rio somar todas as micro-molas tanto em paralelo quanto em s rie. Para isso, necess rio conhecer o n mero de molas conectadas em paralelo.
O n mero de molas conectadas em paralelo pode ser determinado com la seção de elemento ($S$) e la seção microscópica da mola ($s$). O número de molas em paralelo ($N_p$) calculado dividindo la seção de elemento ($S$) por la seção microscópica da mola ($s$):
Para calcular a constante macrosc pica equivalente da constante da mola microsc pica, todas as micro molas devem ser somadas tanto em paralelo quanto em s rie. Para fazer isso, necess rio conhecer, em particular, o n mero de molas conectadas em s rie.
Se desejarmos estimar o número de molas em série ($N_s$), suficiente conhecer o comprimento do corpo ($L$) e o comprimento microscópico da mola ($l$). O número de molas em série ($N_s$) calculado dividindo o comprimento do corpo ($L$) por o comprimento microscópico da mola ($l$):
Para uma barra com um comprimento do corpo ($L$) e ERROR:5352,0, pode-se calcular o número de molas em paralelo ($N_p$) e o número de molas em série ($N_s$) com o comprimento microscópico da mola ($l$) e la seção microscópica da mola ($s$).
Com esses valores, o valor da constante de uma se o inteira pode ser calculado multiplicando por o número de molas em paralelo ($N_p$) com la microscopia constante de Hook ($k_m$). Dessa forma, poss vel calcular la constante de Hooke ($k$) dividindo o valor obtido por o número de molas em série ($N_s$):
$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$
Se as express es para o n mero de elementos forem introduzidas com o comprimento microscópico da mola ($l$) e la seção microscópica da mola ($s$), obtemos a seguinte express o:
A express o para la constante de Hooke ($k$) dada por
possui dois par metros macrosc picos, que s o o comprimento do corpo ($L$) e la seção de elemento ($S$). Os demais, la microscopia constante de Hook ($k_m$), o comprimento microscópico da mola ($l$) e la seção microscópica da mola ($s$), s o microsc picos e, portanto, dependem do material que est sendo descrito. Portanto, faz sentido definir esses fatores como o módulo de Elasticidade ($E$), de modo que:
Como a Lei de Hooke relaciona la força elástica ($F_k$) atrav s de la constante de Hooke ($k$) e la alongamento ($u$) da seguinte forma:
poss vel substituir la constante de Hooke ($k$) pela express o microsc pica e, usando a defini o de o módulo de Elasticidade ($E$), obt m-se com o comprimento do corpo ($L$) e la seção de elemento ($S$) que:
ID:(1884, 0)