Federmodell unter Kräften
Storyboard 
Im Bereich kleiner Verformungen, in dem die Kräfte zwischen den Atomen des Festkörpers proportional zum Abstand vom Gleichgewichtspunkt sind, kann der Festkörper als eine Reihe miteinander verbundener Massen mit Federn modelliert werden.
ID:(1884, 0)
Federmodell unter Kräften
Storyboard 
Im Bereich kleiner Verformungen, in dem die Kräfte zwischen den Atomen des Festkörpers proportional zum Abstand vom Gleichgewichtspunkt sind, kann der Festkörper als eine Reihe miteinander verbundener Massen mit Federn modelliert werden.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wie die Gesamte Hook-Konstante paralleler Federn ($k_p$) von die Hook Konstant der Feder i ($k_i$) ist
ergibt sich, dass im Fall von die Mikroskopische Hook-Konstante ($k_m$) gleich
$k_p = N_p k_m$
die Gesamte Hook-Konstante paralleler Federn ($k_p$) in diesem Fall der Hook'sche Konstante eines monoatomaren Dickenabschnitts entspricht. Um die Konstante f r den gesamten K rper zu erhalten, m ssen alle Abschnitte in Serie summiert werden, und daf r verwenden wir die Beziehung f r die Summe von die Insgesamt Haken Constant von Federn in Serie ($k_s$), wie sie in
gegeben ist.
Mit der Anzahl der Abschnitte, die gleich der Anzahl der Federn in Serie ($N_s$) sind, und wenn wir annehmen, dass sie alle gleich sind, erhalten wir
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
was bedeutet
$k = \displaystyle\frac{N_p}{N_s}k_m$
Schlie lich, mit den Beziehungen f r der Körperlänge ($L$) und der Mikroskopische Länge des Frühlings ($l$)
und mit die Körper Sektion ($S$) und die Mikroskopische Abschnitt des Frühlings ($s$)
erhalten wir schlie lich
Wenn wir Kr fte die Kraft ($F$) an den Enden der Federn anwenden, werden die Federn sich um die Federdehnung i ($u_i$) bzw. Die Hook Konstant der Feder i ($k_i$) verl ngern (oder komprimieren). Wenn der Kontaktpunkt zwischen beiden Federn ruht, muss die Summe der auf ihn wirkenden Kr fte null ergeben, das hei t, sie m ssen gleich die Kraft ($F$) sein. Daher muss f r jede Feder $i$ gelten:
$F = k_iu_i$
Die Gesamtdehnung wird gleich der Summe der einzelnen Dehnungen sein:
$u = \displaystyle\sum_iu_i$
Und unter Verwendung des Hookschen Gesetzes wird dies ausgedr ckt als:
$u = \displaystyle\sum_i\frac{F}{k_i}$
Wenn wir eine Gesamtkonstante f r den Fall einer Reihenschaltung die Insgesamt Haken Constant von Federn in Serie ($k_s$) einf hren, sodass
$F = k_su$
Dann haben wir:
Mit dem Hookeschen Gesetz f r die Federkraft ($F_k$), die Hookes Konstante ($k$) und die Verlängerung ($u$) wie folgt:
und dem Ausdruck f r die Hookes Konstante ($k$) in Bezug auf der Körperlänge ($L$), die Körper Sektion ($S$), der Mikroskopische Länge des Frühlings ($l$), die Mikroskopische Abschnitt des Frühlings ($s$) und die Mikroskopische Hook-Konstante ($k_m$):
in Kombination mit dem Ausdruck f r der Elastizitätsmodul ($E$):
ergibt sich:
Da jede Feder der gleichen angewandten Kraft die Kraft ($F$) ausgesetzt ist, werden die Federn mit den Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) sich jeweils um die Betr ge die Federdehnung 1 ($u_1$) und die Federdehnung 2 ($u_2$) verformen, gem den folgenden Gleichungen:
$F = k_1u_1$
$F = k_2u_2$
Die Gesamtdehnung ergibt sich aus der Summe beider Dehnungen:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Daher verh lt sich das System, als ob es eine Federkonstante h tte, die gleich ist:
Da jede Feder eine unterschiedliche Federkonstante haben kann, die durch die Hook Konstant der Feder i ($k_i$) dargestellt wird, variiert auch die von jeder Feder beigesteuerte Kraft. Gem dem Hooke'schen Gesetz lassen sich die Kr fte $F_i$ wie folgt ausdr cken:
$F_i = k_i u$
Da die Gesamtkraft $F$ der Summe der einzelnen Kr fte entspricht, ergibt sich:
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
Daher kann eine Gesamtfederkonstante definiert werden:
Da jede Feder der gleichen ERROR:5343,0 ausgesetzt ist, werden die Kr fte unterschiedlich sein, wenn die Federkonstanten unterschiedlich sind. Daher, wenn die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) die Federkonstanten sind, werden die Kr fte wie folgt sein:
$F_1 = k_1 u$
$F_2 = k_2 u$
Als Ergebnis ergibt sich die Gesamtkraft:
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Daher verh lt sich das System, als ob es eine Federkonstante h tte, die gleich ist:
Beispiele
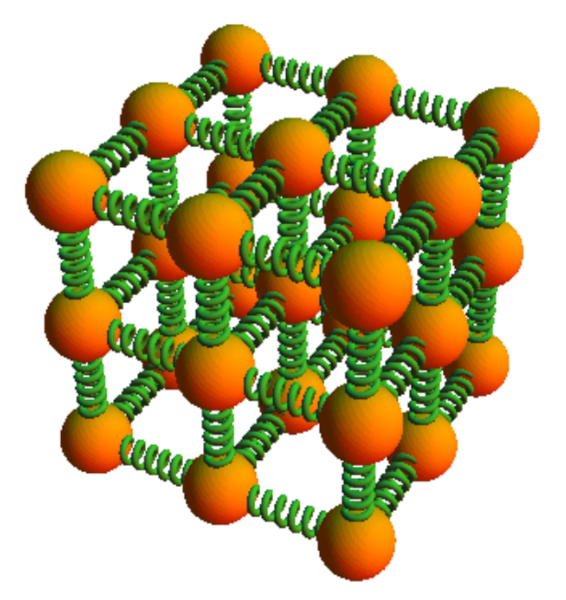
Die Wechselwirkung zwischen den Atomen, die einen Festk rper bilden, ist so beschaffen, dass jedes Atom im Gleichgewicht ist, das bedeutet, die Summe aller Kr fte von seinen Nachbarn ist null. Wenn ein Atom aus dieser Gleichgewichtsposition verschoben wird, ist die Summe nicht mehr null. In einer ersten N herung kann angenommen werden, dass f r kleine Verschiebungen die Kraft proportional zur Entfernung von der Gleichgewichtsposition ist. Dar ber hinaus hnelt die Kraft, die von der zur ckgelegten Strecke abh ngt, der einer Feder. Mit anderen Worten: Atome in einem Festk rper verhalten sich bei kleinen Verformungen so, als w ren sie durch Federn miteinander verbunden:
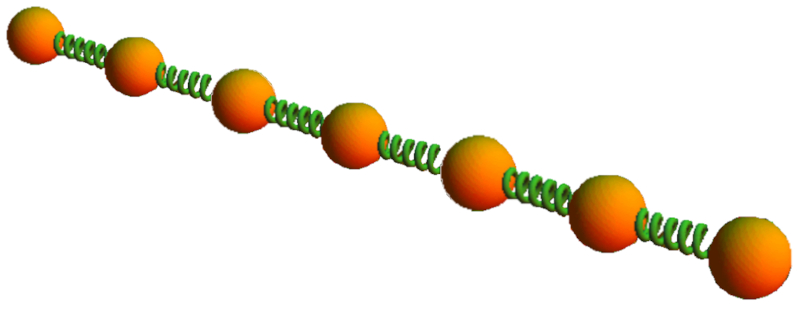
Wenn Sie das Verhalten eines Festk rpers unter Einwirkung einer Kraft modellieren m chten, k nnen Sie zun chst das Verhalten einer Teileinheit in Betracht ziehen, wie zum Beispiel zwei hintereinander geschaltete Federn, wie in der Abbildung gezeigt:
Diese Art der Anordnung der Federn wird als in Serie bezeichnet. Sie zeichnet sich dadurch aus, dass die Kraft die Kraft ($F$) in beiden Federn gleich ist und sie sich gem die Hookes Konstante ($k$) verformen. Daher wird die quivalente Federkonstante die Verlängerung ($u$) als Summe von die Federdehnung 1 ($u_1$) und die Federdehnung 2 ($u_2$) berechnet, die wiederum nach dem Hooke'schen Gesetz:
gleich die Kraft ($F$) geteilt durch die Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) ist:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Daher kann das System aus zwei Federn als eine einzige Feder behandelt werden, deren quivalente Federkonstante die Insgesamt Haken Constant von Federn in Serie ($k_s$) wie folgt berechnet wird:
Im Fall von zwei Federn mit den Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), die durch eine einzelne Feder mit einer Konstanten die Insgesamt Haken Constant von Federn in Serie ($k_s$) modelliert werden k nnen, die mithilfe der folgenden Gleichung berechnet wird:
F r den allgemeineren Fall von Federn mit Konstanten ERROR:10228,0 kann die Gleichung wie folgt verallgemeinert werden:
Dadurch k nnen wir eine Makrostruktur auf folgende Weise modellieren:
Wenn man modellieren m chte, wie sich ein Festk rper unter dem Einfluss einer Kraft verformt, kann man zun chst das Verhalten einer Teilkomponente betrachten, wie zum Beispiel zwei Federn, die nebeneinander verbunden sind, wie in der Abbildung gezeigt:
Diese Art der Anordnung der Federn wird als parallel bezeichnet. Sie zeichnet sich dadurch aus, dass die Verlängerung ($u$) in beiden Federn gleich ist und jede Feder ERROR:4975,0 gem die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) nach dem Hooke'schen Gesetz beitr gt:
Daraus folgt:
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Daher kann das System aus zwei Federn als eine einzige Feder behandelt werden, deren quivalente Federkonstante die Gesamte Hook-Konstante paralleler Federn ($k_p$) wie folgt berechnet wird:
Im Fall von zwei Federn mit den Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), die durch eine einzige Feder mit einer Konstanten die Gesamte Hook-Konstante paralleler Federn ($k_p$) modelliert werden k nnen, die mithilfe der folgenden Gleichung berechnet wird:
F r den allgemeineren Fall von Federn mit Konstanten ERROR:10228,0 kann die Gleichung wie folgt verallgemeinert werden:
Dies erm glicht es uns, eine Makrostruktur wie folgt zu modellieren:
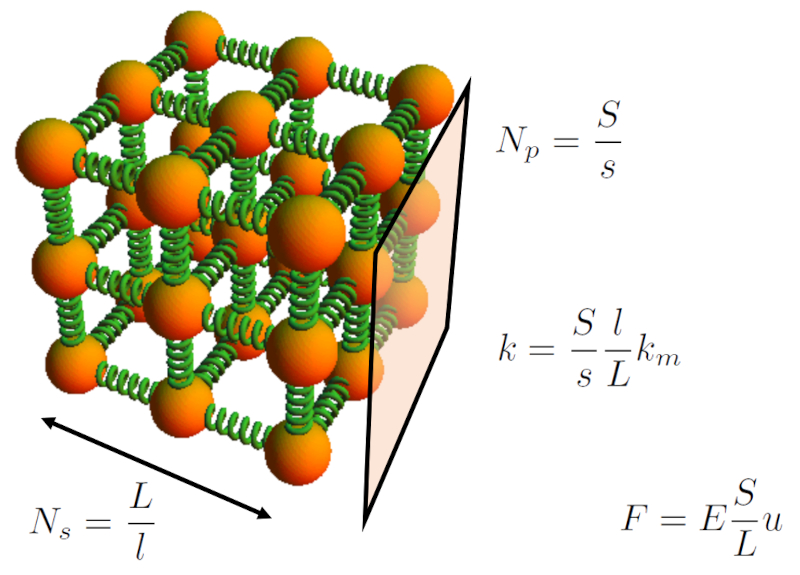
Der Festk rper wird als Netzwerk von Federn modelliert, deren Anzahl basierend auf der Körperlänge ($L$) und die Körper Sektion ($S$) in Bezug auf der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) abgesch tzt wird.
Gem dieser Struktur werden die Federn von die Mikroskopische Hook-Konstante ($k_m$) zuerst parallel ber die Körper Sektion ($S$) summiert, gefolgt von der Serienaddition entlang von ERROR:5355,0.
Das Ergebnis wird dann in das Hookesche Gesetz f r die Federkraft ($F_k$), die Hookes Konstante ($k$) und die Federkraft ($F_k$) mit der Gleichung eingesetzt:
was die Gleichung f r die longitudinale Deformation eines Festk rpers an der elastischen Grenze ergibt:
Wenn wir zwei Widerst nde mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) in Serie schalten, addieren sich die Dehnungen, wodurch jeder einzelne Widerstand basierend auf seinem Kehrwert wirkt. Auf diese Weise ist der Kehrwert von die Insgesamt Haken Constant von Federn in Serie ($k_s$) gleich der Summe der Kehrwerte der individuellen Konstanten die Hook Konstant der Feder i ($k_i$):
In dem Fall von zwei Widerst nden mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), wenn sie parallel geschaltet sind, verhalten sie sich so, als ob es einen quivalenten Widerstand die Insgesamt Haken Constant von Federn in Serie ($k_s$) g be, der gem der folgenden Gleichung berechnet wird:
Dieses Konzept kann f r die Hook Konstant der Feder i ($k_i$) wie folgt verallgemeinert werden:
Wenn Sie zwei Widerst nde mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) parallel schalten, addieren sich ihre Effekte, sodass sie sich wie ein quivalenter Widerstand die Gesamte Hook-Konstante paralleler Federn ($k_p$) verhalten, der gleich der Summe der individuellen Konstanten ist:
F r den Fall von zwei Widerst nden mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), wenn sie parallel geschaltet sind, verhalten sie sich so, als g be es einen quivalenten Widerstand die Gesamte Hook-Konstante paralleler Federn ($k_p$), der durch die folgende Gleichung gegeben ist:
Dieses Konzept kann f r die Hook Konstant der Feder i ($k_i$) verallgemeinert werden als:
Um die makroskopische quivalente der mikroskopischen Federkonstanten zu berechnen, m ssen alle Mikrofedern sowohl in Reihe als auch parallel addiert werden. Daf r muss man insbesondere die Anzahl der in Parallel geschalteten Federn kennen.
Die Anzahl der in Parallel geschalteten Federn kann mit die Körper Sektion ($S$) und die Mikroskopische Abschnitt des Frühlings ($s$) bestimmt werden. Der Anzahl der Federn in Parallel ($N_p$) wird durch die Division von die Körper Sektion ($S$) durch die Mikroskopische Abschnitt des Frühlings ($s$) berechnet:
Um die makroskopische quivalente der mikroskopischen Federkonstante zu berechnen, m ssen alle Mikrofedern sowohl in Parallel- als auch in Reihenschaltung addiert werden. Daf r ist es erforderlich, insbesondere die Anzahl der in Serie geschalteten Federn zu kennen.
Wenn wir der Anzahl der Federn in Serie ($N_s$) sch tzen m chten, gen gt es, der Körperlänge ($L$) und der Mikroskopische Länge des Frühlings ($l$) zu kennen. Der Anzahl der Federn in Serie ($N_s$) wird durch Division von der Körperlänge ($L$) durch der Mikroskopische Länge des Frühlings ($l$) berechnet:
F r eine Stange mit ERROR:5355.1 und die Körper Sektion ($S$) k nnen Sie der Anzahl der Federn in Parallel ($N_p$) und der Anzahl der Federn in Serie ($N_s$) mit der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) berechnen. Mit diesen Werten k nnen Sie die Federkonstante f r einen gesamten Abschnitt berechnen, indem Sie mit der Anzahl der Federn in Parallel ($N_p$) und die Mikroskopische Hook-Konstante ($k_m$) multiplizieren. Auf diese Weise k nnen Sie die Hookes Konstante ($k$) berechnen, indem Sie den erhaltenen Wert durch der Anzahl der Federn in Serie ($N_s$) teilen:
$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$
Wenn Sie die Ausdr cke f r die Anzahl der Elemente mit der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) einf hren, erhalten Sie den folgenden Ausdruck:
Der Ausdruck f r die Hookes Konstante ($k$) gegeben durch
hat zwei makroskopische Parameter, n mlich der Körperlänge ($L$) und die Körper Sektion ($S$). Die brigen die Mikroskopische Hook-Konstante ($k_m$), der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) sind mikroskopisch und h ngen daher vom beschriebenen Material ab. Daher macht es Sinn, diese Faktoren als der Elastizitätsmodul ($E$) zu definieren, sodass:
Da das Hookesche Gesetz die Federkraft ($F_k$) durch die Hookes Konstante ($k$) und die Verlängerung ($u$) auf folgende Weise in Beziehung setzt:
kann man die Hookes Konstante ($k$) durch den mikroskopischen Ausdruck ersetzen und unter Verwendung der Definition von der Elastizitätsmodul ($E$) ergibt sich mit der Körperlänge ($L$) und die Körper Sektion ($S$), dass:
ID:(1884, 0)