Modèle à ressort sous forces
Storyboard 
À la limite des petites déformations, où les forces entre les atomes du solide sont proportionnelles à la distance par rapport au point d'équilibre, le solide peut être modélisé comme une série de masses interconnectées par des ressorts.
ID:(1884, 0)
Modèle à ressort sous forces
Storyboard 
À la limite des petites déformations, où les forces entre les atomes du solide sont proportionnelles à la distance par rapport au point d'équilibre, le solide peut être modélisé comme une série de masses interconnectées par des ressorts.
Variables
Calculs
Calculs
Équations
Comme a constante de crochet totale des ressorts en parallèle ($k_p$) de a constante de Hook à ressort i ($k_i$) est
il s'ensuit que, dans le cas o a microscopie constante de Hook ($k_m$) est gal
$k_p = N_p k_m$
a constante de crochet totale des ressorts en parallèle ($k_p$) correspond, dans ce cas, la constante de Hook d'une section d' paisseur monoatomique. Pour obtenir la constante pour l'ensemble du corps, il est n cessaire de sommer toutes les sections en s rie, et pour cela, nous travaillons avec la relation pour la somme de a constante de crochet totale des ressorts en série ($k_s$), donn e par
Avec le nombre de sections tant gal le nombre de ressorts en série ($N_s$), et si nous supposons qu'elles sont toutes gales, nous obtenons
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
c'est- -dire
$k = \displaystyle\frac{N_p}{N_s}k_m$
Enfin, avec les relations pour le la longueur du corps ($L$) et le longueur du ressort microscopique ($l$)
et avec a section d'élément ($S$) et a section de ressort microscopique ($s$)
nous obtenons finalement
Lorsque nous appliquons des forces a force ($F$) aux extr mit s des ressorts, les ressorts vont s'allonger (ou se comprimer) de a élongation du ressort je ($u_i$) et a constante de Hook à ressort i ($k_i$) respectivement. Si le point de contact entre les deux ressorts est au repos, la somme des forces qui agissent sur lui doit tre gale z ro, c'est- -dire qu'elles doivent tre gales a force ($F$). Par cons quent, pour chaque ressort $i$, il doit satisfaire
$F = k_iu_i$
L'allongement total sera gal la somme des allongements individuels :
$u = \displaystyle\sum_iu_i$
Et en utilisant la loi de Hooke, cela peut s'exprimer comme suit :
$u = \displaystyle\sum_i\frac{F}{k_i}$
Si nous introduisons une constante totale pour le cas d'une connexion en s rie a constante de crochet totale des ressorts en série ($k_s$), de telle sorte que
$F = k_su$
Alors nous avons :
Avec la loi de Hooke pour a force élastique ($F_k$), a constante de Hooke ($k$) et a élongation ($u$) comme suit :
et l'expression de a constante de Hooke ($k$) en fonction de le la longueur du corps ($L$), a section d'élément ($S$), le longueur du ressort microscopique ($l$), a section de ressort microscopique ($s$) et a microscopie constante de Hook ($k_m$) :
combin e avec l'expression de le module d'élasticité ($E$) :
le r sultat est :
tant donn que chaque ressort est soumis la m me force appliqu e a force ($F$), les ressorts avec les constantes a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) se d forment respectivement de magnitudes a élongation du ressort 1 ($u_1$) et a élongation du ressort 2 ($u_2$), conform ment aux quations suivantes :
$F = k_1u_1$
$F = k_2u_2$
L'allongement total sera la somme des deux allongements :
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Par cons quent, le syst me se comporte comme s'il avait une constante de ressort gale :
tant donn que chaque ressort peut avoir une constante de raideur diff rente, repr sent e par a constante de Hook à ressort i ($k_i$), la force contribu e par chaque ressort varie galement. Selon la loi de Hooke, les forces $F_i$ peuvent tre exprim es comme suit :
$F_i = k_i u$
Comme la force totale $F$ correspond la somme des forces individuelles, nous avons :
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
Par cons quent, une constante de raideur totale peut tre d finie comme suit :
Puisque chaque ressort est soumis la m me ERROR:5343,0, les forces seront diff rentes si les constantes des ressorts le sont. Par cons quent, si a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) sont les constantes des ressorts, les forces seront les suivantes :
$F_1 = k_1 u$
$F_2 = k_2 u$
En cons quence, la force totale sera :
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Ainsi, le syst me se comporte comme s'il avait une constante de ressort gale :
Exemples
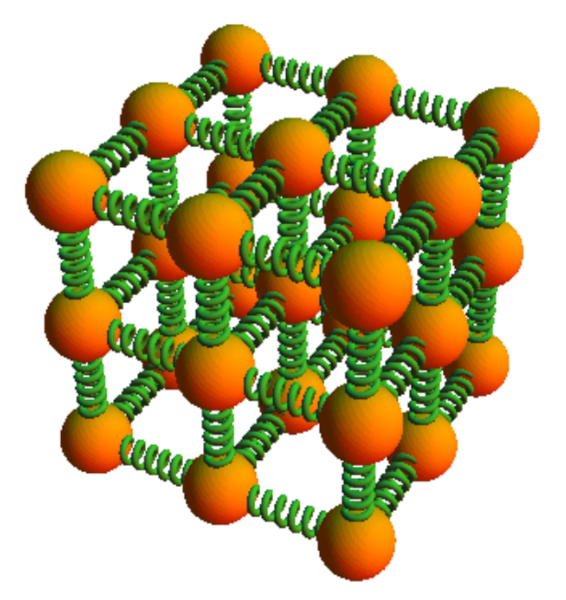
L'interaction entre les atomes constituant un solide est telle que chaque atome se trouve en quilibre, ce qui signifie que la somme de toutes les forces provenant de ses voisins est nulle. Lorsqu'un atome est d plac de sa position d' quilibre, cette somme n'est plus nulle. Dans une premi re approximation, on peut supposer que, pour de petits d placements, la force est proportionnelle la distance par rapport la position d' quilibre. De plus, la force, qui d pend de la distance parcourue, ressemble celle d'un ressort. En d'autres termes, les atomes dans un solide se comportent comme s'ils taient reli s par des ressorts lorsqu'ils sont soumis de petites d formations :
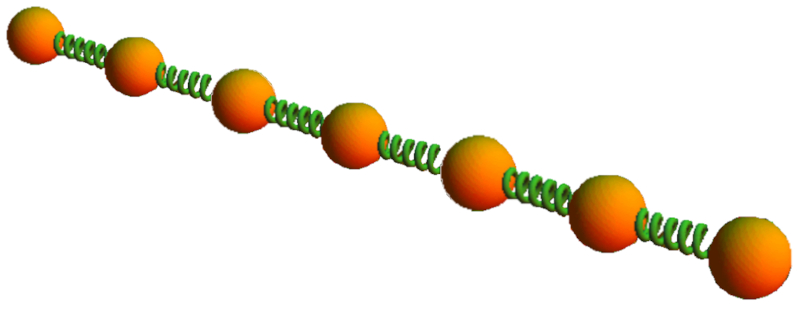
Si vous souhaitez mod liser la d formation d'un solide sous l'influence d'une force, vous pouvez d'abord consid rer le comportement d'une sous-unit , comme deux ressorts connect s l'un derri re l'autre, comme illustr dans l'image :
Ce type d'arrangement des ressorts est appel en s rie. Il se caract rise par le fait que la force a force ($F$) est la m me dans les deux ressorts, et ils se d forment selon a constante de Hooke ($k$). Par cons quent, la constante de raideur quivalente a élongation ($u$) est calcul e comme la somme de a élongation du ressort 1 ($u_1$) et a élongation du ressort 2 ($u_2$), qui, leur tour, selon la loi de Hooke :
est gale a force ($F$) divis par les constantes a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$), respectivement :
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Par cons quent, le syst me de deux ressorts peut tre trait comme un seul ressort dont la constante de raideur quivalente a constante de crochet totale des ressorts en série ($k_s$) est calcul e comme suit :
Dans le cas de deux ressorts avec des constantes a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) qui peuvent tre mod lis s par un seul ressort avec une constante a constante de crochet totale des ressorts en série ($k_s$) calcul e l'aide de l' quation suivante :
Pour le cas plus g n ral de ressorts avec des constantes ERROR:10228,0, l' quation peut tre g n ralis e comme suit :
Cela nous permet de mod liser une structure macro de la mani re suivante :
Si l'on souhaite mod liser la d formation d'un solide sous l'influence d'une force, on peut d'abord consid rer le comportement d'une sous-unit , telle que deux ressorts connect s c te c te, comme illustr dans l'image :
Ce type d'agencement des ressorts est appel en parall le. Il se caract rise par le fait que a élongation ($u$) est le m me pour les deux ressorts et que chaque ressort contribue ERROR:4975,0 en fonction de a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) selon la loi de Hooke :
Par cons quent, on a :
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Ainsi, le syst me de deux ressorts peut tre trait comme un seul ressort dont la constante lastique quivalente a constante de crochet totale des ressorts en parallèle ($k_p$) est calcul e de la mani re suivante :
Dans le cas de deux ressorts avec des constantes a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) qui peuvent tre mod lis s par un seul ressort avec une constante a constante de crochet totale des ressorts en parallèle ($k_p$) calcul e l'aide de l' quation suivante :
Pour le cas plus g n ral de ressorts avec des constantes ERROR:10228,0, l' quation peut tre g n ralis e comme suit :
Cela nous permet de mod liser une structure macro de la mani re suivante :
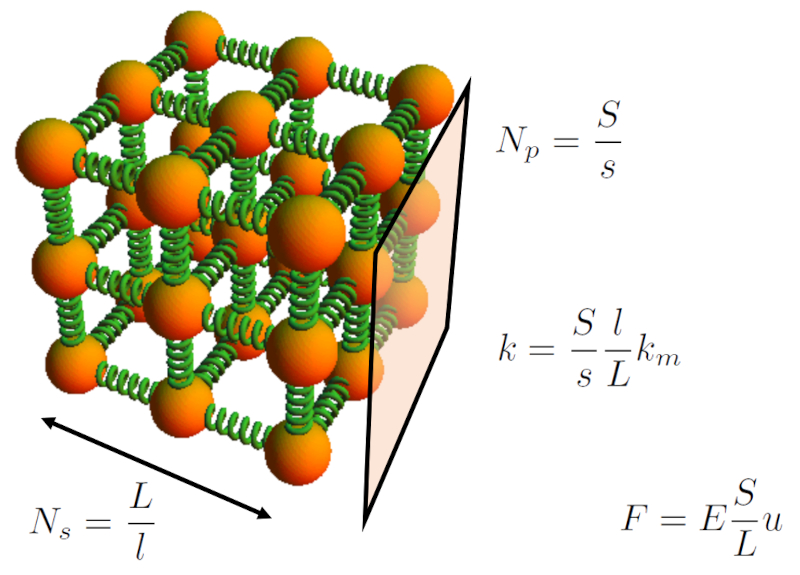
Le solide est mod lis comme un r seau de ressorts dont la quantit est estim e en fonction de le la longueur du corps ($L$) et a section d'élément ($S$) par rapport le longueur du ressort microscopique ($l$) et a section de ressort microscopique ($s$).
Selon cette structure, les ressorts de a microscopie constante de Hook ($k_m$) sont d'abord additionn s en parall le sur a section d'élément ($S$), suivis par une addition en s rie le long de ERROR:5355,0.
Le r sultat est ensuite introduit dans la loi de Hooke pour a force élastique ($F_k$), a constante de Hooke ($k$) et a force élastique ($F_k$) en utilisant l' quation :
ce qui donne l' quation pour la d formation longitudinale d'un solide la limite lastique :
Si nous avons deux r sistances avec des valeurs a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) connect es en s rie, les allongements s'additionnent, ce qui fait que chaque r sistance individuelle agit en fonction de son inverse. De cette mani re, l'inverse de a constante de crochet totale des ressorts en série ($k_s$) est gal la somme des inverses des constantes individuelles a constante de Hook à ressort i ($k_i$) :
Dans le cas de deux r sistances ayant des valeurs a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$), lorsqu'elles sont connect es en parall le, elles agissent comme s'il y avait une r sistance quivalente a constante de crochet totale des ressorts en série ($k_s$) donn e par l' quation suivante :
Ce concept peut tre g n ralis pour a constante de Hook à ressort i ($k_i$) comme suit :
Si vous avez deux r sistances avec les valeurs a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$) connect es en parall le, leurs effets s'additionnent, agissant comme s'il y avait une r sistance quivalente a constante de crochet totale des ressorts en parallèle ($k_p$) gale la somme des constantes individuelles :
Dans le cas de deux r sistances avec des valeurs a constante de Hook à ressort 1 ($k_1$) et a constante de Hook à ressort 2 ($k_2$), lorsqu'elles sont connect es en parall le, elles se comportent comme s'il y avait une r sistance quivalente a constante de crochet totale des ressorts en parallèle ($k_p$) donn e par l' quation suivante :
Ce concept peut tre g n ralis pour a constante de Hook à ressort i ($k_i$) comme suit :
Pour calculer l' quivalent macroscopique de la constante de ressort microscopique, il faut additionner tous les micro ressorts la fois en parall le et en s rie. Pour ce faire, il est n cessaire de conna tre en particulier le nombre de ressorts connect s en parall le.
Le nombre de ressorts connect s en parall le peut tre d termin avec a section d'élément ($S$) et a section de ressort microscopique ($s$). Le nombre de ressorts en parallèle ($N_p$) est calcul en divisant a section d'élément ($S$) par a section de ressort microscopique ($s$) :
Pour calculer la constante macroscopique quivalente de la constante de ressort microscopique, toutes les micro-ressorts doivent tre additionn s la fois en parall le et en s rie. Pour ce faire, il est n cessaire de conna tre, en particulier, le nombre de ressorts connect s en s rie.
Si nous souhaitons estimer le nombre de ressorts en série ($N_s$), il suffit de conna tre le la longueur du corps ($L$) et le longueur du ressort microscopique ($l$). Le nombre de ressorts en série ($N_s$) est calcul en divisant le la longueur du corps ($L$) par le longueur du ressort microscopique ($l$) :
Pour une barre avec ERROR:5355.1 et a section d'élément ($S$), vous pouvez calculer le nombre de ressorts en parallèle ($N_p$) et le nombre de ressorts en série ($N_s$) en utilisant le longueur du ressort microscopique ($l$) et a section de ressort microscopique ($s$). Avec ces valeurs, vous pouvez calculer la constante de ressort pour toute une section en multipliant par le nombre de ressorts en parallèle ($N_p$) avec a microscopie constante de Hook ($k_m$). De cette mani re, vous pouvez calculer a constante de Hooke ($k$) en divisant la valeur obtenue par le nombre de ressorts en série ($N_s$) :
$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$
Si vous introduisez les expressions pour le nombre d' l ments avec le longueur du ressort microscopique ($l$) et a section de ressort microscopique ($s$), vous obtenez l'expression suivante :
L'expression pour a constante de Hooke ($k$) donn e par
comprend deux param tres macroscopiques, qui sont le la longueur du corps ($L$) et a section d'élément ($S$). Les autres, a microscopie constante de Hook ($k_m$), le longueur du ressort microscopique ($l$) et a section de ressort microscopique ($s$), sont microscopiques et d pendent donc du mat riau d crit. Par cons quent, il est logique de d finir ces facteurs comme le module d'élasticité ($E$), de sorte que :
Comme la loi de Hooke relie a force élastique ($F_k$) travers a constante de Hooke ($k$) et a élongation ($u$) de la mani re suivante :
vous pouvez remplacer a constante de Hooke ($k$) par l'expression microscopique et en utilisant la d finition de le module d'élasticité ($E$), vous obtenez avec le la longueur du corps ($L$) et a section d'élément ($S$) que :
ID:(1884, 0)