Spring model under forces
Storyboard 
At the limit of small deformations, where the forces between solid atoms are proportional to the distance from the equilibrium point, the solid can be modeled as a series of interconnected masses with springs.
ID:(1884, 0)
Spring model under forces
Storyboard 
At the limit of small deformations, where the forces between solid atoms are proportional to the distance from the equilibrium point, the solid can be modeled as a series of interconnected masses with springs.
Variables
Calculations
Calculations
Equations
As the the total Hook constant of springs in parallel ($k_p$) of the spring Hook constant i ($k_i$) is
it follows that in the case of the microscopic Hook constant ($k_m$) being equal to
$k_p = N_p k_m$
the total Hook constant of springs in parallel ($k_p$) corresponds, in this case, to the Hook's constant of a monoatomic thickness section. To obtain the constant for the entire body, one must sum all the sections in series, and for this, we work with the relationship for the sum of the total Hook constant of springs in series ($k_s$), given by
With the number of sections being equal to the number of springs in series ($N_s$), and if we assume that they are all equal, we obtain
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
meaning
$k = \displaystyle\frac{N_p}{N_s}k_m$
Finally, with the relationships for the body length ($L$) and the microscopic length of spring ($l$)
and with the body Section ($S$) and the microscopic section of spring ($s$)
we ultimately obtain
When we apply forces the force ($F$) at the ends of the springs, the springs will elongate (or compress) by the spring elongation i ($u_i$) and the spring Hook constant i ($k_i$) respectively. If the point of contact between both springs is at rest, the sum of the forces acting on it must add up to zero, meaning they must be equal to the force ($F$). Therefore, for each spring $i$, it must satisfy
$F = k_iu_i$
The total elongation will be equal to the sum of the individual elongations:
$u = \displaystyle\sum_iu_i$
And using Hooke's law, this can be expressed as:
$u = \displaystyle\sum_i\frac{F}{k_i}$
If we introduce a total constant for the case of a series connection the total Hook constant of springs in series ($k_s$), such that
$F = k_su$
Then we have:
With Hooke's Law for the elastic Force ($F_k$), the hooke Constant ($k$), and the elongation ($u$) as follows:
and the expression for the hooke Constant ($k$) in terms of the body length ($L$), the body Section ($S$), the microscopic length of spring ($l$), the microscopic section of spring ($s$), and the microscopic Hook constant ($k_m$):
combined with the expression for the modulus of Elasticity ($E$):
the result is:
Since each spring is exposed to the same applied force the force ($F$), the springs with constants the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) will deform by magnitudes the spring elongation 1 ($u_1$) and the spring elongation 2 ($u_2$) respectively, according to the following equations:
$F = k_1u_1$
$F = k_2u_2$
The total elongation will be the sum of both elongations:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Therefore, the system behaves as if it had a spring constant equal to:
Since each spring can have a different spring constant, represented by the spring Hook constant i ($k_i$), the force contributed by each spring also varies. According to Hooke's law, the forces $F_i$ can be expressed as:
$F_i = k_i u$
As the total force $F$ corresponds to the sum of individual forces, we have:
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
Therefore, a total spring constant can be defined as:
Since each spring is subjected to the same the elongation ($u$), the forces will be different if the spring constants are different. Therefore, if the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) are the spring constants, the forces will be:
$F_1 = k_1 u$
$F_2 = k_2 u$
As a result, the total force will be:
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Thus, the system behaves as if it had a spring constant equal to:
Examples
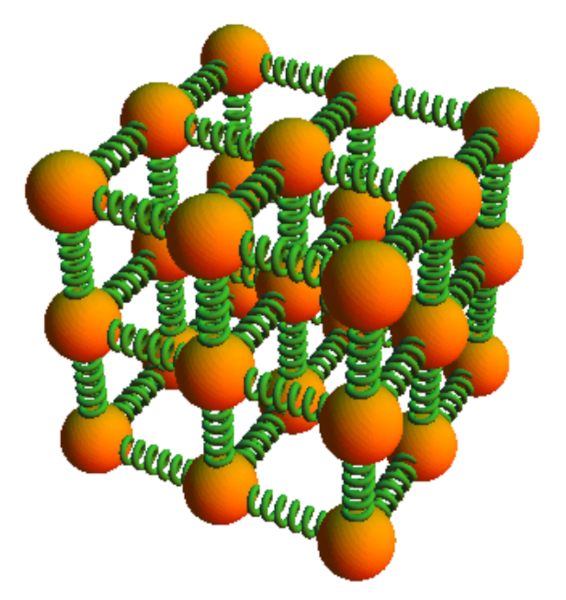
The interaction between the atoms composing a solid is such that each atom is in equilibrium, meaning the sum of all the forces from its neighbors is zero. When an atom is displaced from this equilibrium position, the sum is no longer zero. In a first approximation, it can be assumed that for small displacements, the force is proportional to the distance from the equilibrium point. Furthermore, the force, which depends on the distance traveled, resembles that of a spring. In other words, atoms in a solid behave as if they were connected by springs when subjected to small deformations:
If you want to model how a solid deforms under the influence of a force, you can first consider the behavior of a subunit, such as two springs connected one behind the other, as shown in the image:
This type of arrangement of the springs is called in series. It is characterized by the fact that the force the force ($F$) is the same in both springs, and they deform according to the hooke Constant ($k$). Therefore, the equivalent spring constant the elongation ($u$) is calculated as the sum of the spring elongation 1 ($u_1$) and the spring elongation 2 ($u_2$), which, in turn, by Hooke's law:
is equal to the force ($F$) divided by the constants the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$), respectively:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Therefore, the system of two springs can be treated as a single spring whose equivalent spring constant the total Hook constant of springs in series ($k_s$) is calculated as follows:
In the case of two springs with constants the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) that can be modeled by a single spring with a constant the total Hook constant of springs in series ($k_s$) calculated using the following equation:
For the more general case of springs with constants ERROR:10228,0, the equation can be generalized as follows:
This allows us to model a macro structure in the following way:
If one wishes to model how a solid deforms under the influence of a force, the behavior of a subunit can first be considered, such as two springs connected side by side, as shown in the image:
This type of arrangement of the springs is called in parallel. It is characterized because the elongation ($u$) in both springs is the same and each spring contributes the force ($F$) according to the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) as per Hooke's law:
Thus, it follows that:
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Therefore, the system of two springs can be treated as a single spring whose equivalent spring constant the total Hook constant of springs in parallel ($k_p$) is calculated as follows:
In the case of two springs with constants the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) that can be modeled by a single spring with a constant the total Hook constant of springs in parallel ($k_p$) calculated using the following equation:
For the more general case of springs with constants ERROR:10228,0, the equation can be generalized as follows:
This allows us to model a macro structure as follows:
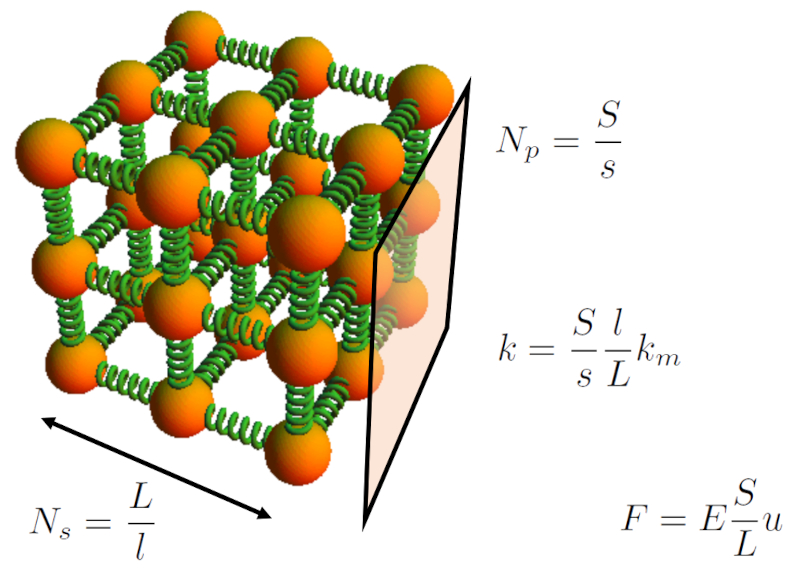
The solid is modeled as a network of springs whose quantity is estimated based on the body length ($L$) and the body Section ($S$) with reference to the microscopic length of spring ($l$) and the microscopic section of spring ($s$).
According to this structure, the springs of the microscopic Hook constant ($k_m$) are first summed in parallel over the body Section ($S$), followed by series summation along ERROR:5355,0.
The result is then plugged into Hooke's law for the elastic Force ($F_k$), the hooke Constant ($k$), and the elastic Force ($F_k$) using the equation:
yielding the equation for the longitudinal deformation of a solid at the elastic limit:
If we have two resistors with values the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) connected in series, the extensions add up, causing each individual resistor to act based on its inverse. In this way, the inverse of the total Hook constant of springs in series ($k_s$) is equal to the sum of the inverses of the individual constants the spring Hook constant i ($k_i$):
In the case of two resistors with values the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$), when they are connected in parallel, they act as if there were an equivalent resistance the total Hook constant of springs in series ($k_s$) given by the following equation:
This concept can be generalized for the spring Hook constant i ($k_i$) as:
If you have two resistors with values the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$) connected in parallel, their effects add up, acting as if there were an equivalent resistance the total Hook constant of springs in parallel ($k_p$) equal to the sum of the individual constants:
For the case of two resistors with values the spring Hook constant 1 ($k_1$) and the spring Hook constant 2 ($k_2$), when they are connected in parallel, they act as if there were an equivalent resistance the total Hook constant of springs in parallel ($k_p$) given by the following equation:
This concept can be generalized for the spring Hook constant i ($k_i$) as:
To calculate the macroscopic equivalent of the microscopic spring constant, one must sum all the microsprings both in parallel and in series. To do this, it is necessary to know the number of springs connected in parallel.
The number of springs connected in parallel can be determined with the body Section ($S$) and the microscopic section of spring ($s$). The number of springs in parallel ($N_p$) is calculated by dividing the body Section ($S$) by the microscopic section of spring ($s$):
To calculate the macroscopic equivalent constant of the microscopic spring constant, all microsprings must be added both in parallel and in series. To do this, it is necessary to know, in particular, the number of springs connected in series.
If we want to estimate the number of springs in series ($N_s$), it is sufficient to know the body length ($L$) and the microscopic length of spring ($l$). The number of springs in series ($N_s$) is calculated by dividing the body length ($L$) by the microscopic length of spring ($l$):
For a bar with ERROR:5355.1 and the body Section ($S$), you can calculate the number of springs in parallel ($N_p$) and the number of springs in series ($N_s$) using the microscopic length of spring ($l$) and the microscopic section of spring ($s$). With these values, you can calculate the spring constant for an entire section by multiplying by the number of springs in parallel ($N_p$) using the microscopic Hook constant ($k_m$). This way, you can calculate the hooke Constant ($k$) by dividing the obtained value by the number of springs in series ($N_s$):
$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$
If you introduce the expressions for the number of elements with the microscopic length of spring ($l$) and the microscopic section of spring ($s$), you get the following expression:
The expression for the hooke Constant ($k$) given by
has two macroscopic parameters, which are the body length ($L$) and the body Section ($S$). The remaining the microscopic Hook constant ($k_m$), the microscopic length of spring ($l$), and the microscopic section of spring ($s$) are microscopic and thus depend on the material being described. Therefore, it makes sense to define these factors as the modulus of Elasticity ($E$), so that:
As Hooke's Law relates the elastic Force ($F_k$) through the hooke Constant ($k$) and the elongation ($u$) in the following manner:
you can replace the hooke Constant ($k$) with the microscopic expression and using the definition of the modulus of Elasticity ($E$), you obtain with the body length ($L$) and the body Section ($S$) that:
ID:(1884, 0)