Modelo de resorte bajo fuerzas
Storyboard 
En el límite de deformaciones pequeñas, donde las fuerzas entre átomos del sólido son proporcionales a la distancia respecto al punto de equilibrio, el sólido puede representarse como una serie de masas interconectadas mediante resortes.
ID:(1884, 0)
Modelo de resorte bajo fuerzas
Storyboard 
En el límite de deformaciones pequeñas, donde las fuerzas entre átomos del sólido son proporcionales a la distancia respecto al punto de equilibrio, el sólido puede representarse como una serie de masas interconectadas mediante resortes.
Variables
Cálculos
Cálculos
Ecuaciones
Como la la constante de Hook total de resortes en paralelo ($k_p$) de la constante de Hook de resorte i ($k_i$) es
se tiene que para el caso de la constante de Hook microscópica ($k_m$) iguales que
$k_p = N_p k_m$
la constante de Hook total de resortes en paralelo ($k_p$) corresponde, en este caso, a la constante de Hook de una secci n de un grosor monoat mico. Para obtener la constante de todo el cuerpo, se debe sumar ahora en serie todas las secciones, para lo que se trabaja con la relaci n para la suma de la constante de Hook total de resortes en serie ($k_s$), dada por
Con el n mero de secciones igual a el número de resortes en serie ($N_s$), y si se asume que todas son iguales, se obtiene
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
o sea
$k = \displaystyle\frac{N_p}{N_s}k_m$
Finalmente, con las relaciones para el largo del cuerpo ($L$) y el largo del resorte microscópico ($l$)
y con la sección del elemento ($S$) y la sección del resorte microscópico ($s$)
se obtiene finalmente
Cuando aplicamos fuerzas la fuerza ($F$) en los extremos de los resortes, los resortes se elongar n (o comprimir n) en la elongación del resorte i ($u_i$) y la constante de Hook de resorte i ($k_i$) respectivamente. Si el punto de contacto entre ambos resortes est en reposo, la suma de las fuerzas que act an sobre l debe ser igual a cero, es decir, deben ser iguales a la fuerza ($F$). Por lo tanto, en cada resorte $i$ debe cumplirse que
$F = k_iu_i$
La elongaci n total ser igual a la suma de las elongaciones individuales:
$u = \displaystyle\sum_iu_i$
Y utilizando la ley de Hooke, esto se expresa como:
$u = \displaystyle\sum_i\frac{F}{k_i}$
Si introducimos una constante total para el caso de conexi n en serie la constante de Hook total de resortes en serie ($k_s$), tal que
$F = k_su$
Entonces, se tiene:
Con la Ley de Hooke para la fuerza elástica ($F_k$), la constante de Hooke ($k$) y la elongación ($u$) de la siguiente forma:
y la expresi n para la constante de Hooke ($k$) en funci n de el largo del cuerpo ($L$), la sección del elemento ($S$), el largo del resorte microscópico ($l$), la sección del resorte microscópico ($s$) y la constante de Hook microscópica ($k_m$):
combinada con la expresi n para el módulo de Elasticidad ($E$):
el resultado es:
Dado que cada resorte est expuesto a la misma fuerza aplicada la fuerza ($F$), los resortes con constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) se deformar n en magnitudes la elongación del resorte 1 ($u_1$) y la elongación del resorte 2 ($u_2$) respectivamente, de acuerdo con las siguientes ecuaciones:
$F = k_1u_1$
$F = k_2u_2$
La elongaci n total ser la suma de ambas elongaciones:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Por lo tanto, el sistema se comporta como si tuviera una constante de resorte igual a:
Dado que cada resorte puede tener una constante de elasticidad distinta, representada por la constante de Hook de resorte i ($k_i$), la fuerza que cada resorte aporta tambi n var a. Seg n la ley de Hooke, las fuerzas $F_i$ se expresan como:
$F_i = k_i u$
Dado que la fuerza total $F$ es la suma de las fuerzas individuales, se obtiene:
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
De esta manera, se puede definir una constante de elasticidad total:
Dado que cada resorte est sujeto a la misma ERROR:5343,0, las fuerzas ser n diferentes si las constantes lo son. Por lo tanto, si la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) son las constantes, las fuerzas ser n las siguientes:
$F_1 = k_1 u$
$F_2 = k_2 u$
Como resultado, la fuerza total ser :
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Por lo tanto, el sistema se comporta como si tuviera una constante de resorte igual a:
Ejemplos
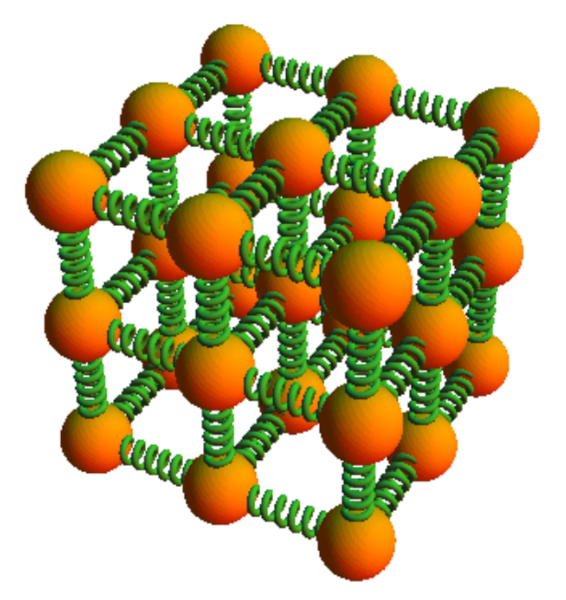
La interacci n entre los tomos que componen un s lido es tal que cada tomo se encuentra en equilibrio, lo que significa que la suma de todas las fuerzas ejercidas por sus vecinos sobre l es nula. Cuando se desplaza el tomo de su posici n de equilibrio, esta suma deja de ser nula. En una primera aproximaci n, se puede asumir que para desplazamientos peque os, la fuerza es proporcional a la distancia desde la posici n de equilibrio. Adem s, la fuerza que depende de la distancia recorrida se asemeja a la de un resorte. En otras palabras, los tomos en un s lido se comportan como si estuvieran conectados por resortes cuando se someten a peque as deformaciones:
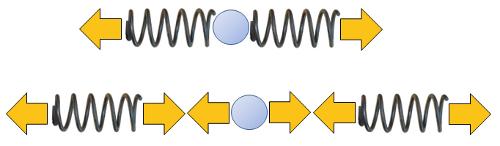
Si se desea modelar c mo se deforma un s lido bajo la influencia de una fuerza, primero se puede considerar el comportamiento de una subunidad, como dos resortes conectados uno detr s del otro, como se muestra en la imagen:
Este tipo de disposici n de los resortes se llama en serie. Se caracteriza porque la fuerza la fuerza ($F$) es igual en ambos resortes, y estos se deforman seg n la constante de Hooke ($k$). Por lo tanto, la constante el stica equivalente la elongación ($u$) se calcula como la suma de la elongación del resorte 1 ($u_1$) y la elongación del resorte 2 ($u_2$), que a su vez, seg n la ley de Hooke:
es igual a la fuerza ($F$) dividido por las constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$), respectivamente:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Por lo tanto, el sistema de dos resortes se puede tratar como un solo resorte cuya constante el stica equivalente la constante de Hook total de resortes en serie ($k_s$) se calcula de la siguiente manera:
En el caso de dos resortes con constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) que pueden ser modelados por un nico resorte con una constante la constante de Hook total de resortes en serie ($k_s$) calculada mediante la siguiente ecuaci n:
Para el caso m s general de resortes con constantes ERROR:10228,0, la ecuaci n puede generalizarse de la siguiente manera:
Con esto, se puede modelar una estructura macro en la siguiente forma:
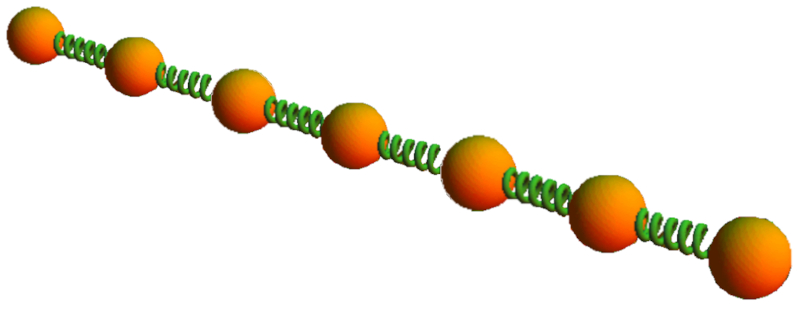
Si se desea modelar c mo se deforma un s lido bajo la influencia de una fuerza, primero se puede considerar el comportamiento de una subunidad, como dos resortes conectados uno al lado del otro, como se muestra en la imagen:
Este tipo de disposici n de los resortes se llama en paralelo. Se caracteriza porque la elongación ($u$) en ambos resortes es la misma y cada resorte aporta ERROR:4975,0 en funci n de la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) seg n la ley de Hooke:
Por ello se tiene que:
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Por lo tanto, el sistema de dos resortes se puede tratar como un solo resorte cuya constante el stica equivalente la constante de Hook total de resortes en paralelo ($k_p$) se calcula de la siguiente manera:
En el caso de dos resortes con constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) que pueden ser modelados por un nico resorte con una constante la constante de Hook total de resortes en paralelo ($k_p$) calculada mediante la siguiente ecuaci n:
Para el caso m s general de resortes con constantes ERROR:10228,0, la ecuaci n puede generalizarse de la siguiente manera:
Esto nos permite modelar una estructura macro de la siguiente manera:
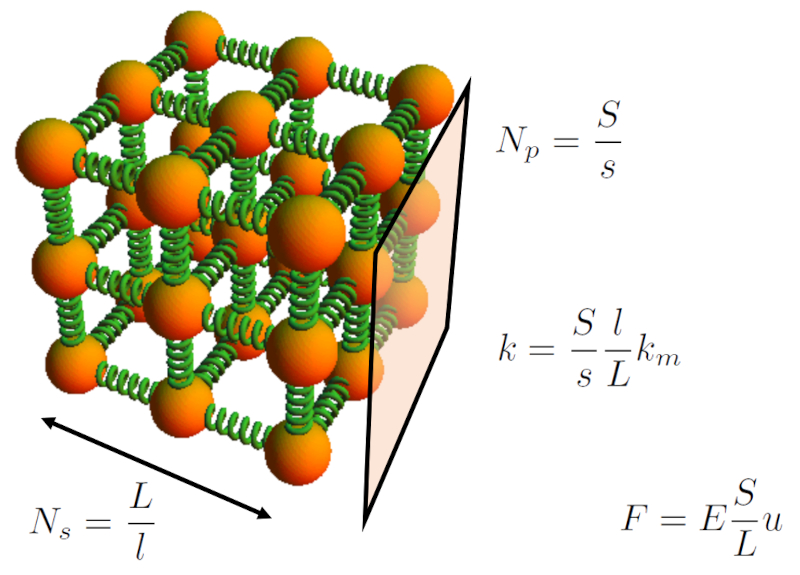
El s lido se modela como una red de resortes cuya cantidad se estima en funci n de el largo del cuerpo ($L$) y la sección del elemento ($S$) bas ndose en el largo del resorte microscópico ($l$) y la sección del resorte microscópico ($s$).
Conforme a esta estructura, se suman inicialmente los resortes de la constante de Hook microscópica ($k_m$) en paralelo sobre la sección del elemento ($S$), y luego se procede con la suma en serie a lo largo de ERROR:5355,0.
El resultado se introduce en la ley de Hooke para la fuerza elástica ($F_k$), la constante de Hooke ($k$) y la fuerza elástica ($F_k$) mediante la ecuaci n:
lo que da lugar a la ecuaci n para la deformaci n longitudinal de un s lido en el l mite el stico:
Si tenemos dos resistencias con valores la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) conectadas en serie, las elongaciones se suman, lo que hace que cada resistencia individual act e en funci n de su inverso. De esta manera, el inverso de la constante de Hook total de resortes en serie ($k_s$) es igual a la suma de los inversos de las constantes individuales la constante de Hook de resorte i ($k_i$):
En el caso de dos resistencias con valores la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$), cuando est n conectadas en paralelo, act an como si hubiera una resistencia equivalente la constante de Hook total de resortes en serie ($k_s$) que se calcula utilizando la siguiente ecuaci n:
Este concepto se puede generalizar para la constante de Hook de resorte i ($k_i$) de la siguiente manera:
Si tenemos dos resistencias con valores la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) conectadas en paralelo, sus efectos se suman, actuando como si existiera una resistencia equivalente la constante de Hook total de resortes en paralelo ($k_p$) que es igual a la suma de las constantes individuales:
En el caso de dos resistencias con valores la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$), cuando est n conectadas en paralelo, act an como si hubiera una resistencia equivalente la constante de Hook total de resortes en paralelo ($k_p$) dada por la siguiente ecuaci n:
Este concepto se puede generalizar para la constante de Hook de resorte i ($k_i$) como:
Para calcular la constante macrosc pica equivalente de la constante de Hook microsc pica, se deben sumar todos los micro resortes tanto en paralelo como en serie. Para ello, es necesario conocer en particular el n mero de resortes conectados en paralelo.
El n mero de resortes que est n conectados en paralelo se puede determinar con la sección del elemento ($S$) y la sección del resorte microscópico ($s$). El número de resortes en paralelo ($N_p$) se calcula dividiendo la sección del elemento ($S$) por la sección del resorte microscópico ($s$):
Para calcular la constante macrosc pica equivalente de la constante de resorte microsc pico, se deben sumar todos los micro resortes tanto en paralelo como en serie. Para hacerlo, es necesario conocer en particular el n mero de resortes conectados en serie.
Si deseamos estimar el número de resortes en serie ($N_s$), basta con conocer el largo del cuerpo ($L$) y el largo del resorte microscópico ($l$). El número de resortes en serie ($N_s$) se calcula dividiendo el largo del cuerpo ($L$) por el largo del resorte microscópico ($l$):
Para una barra con un largo del cuerpo ($L$) y ERROR:5352,0, se puede calcular el número de resortes en paralelo ($N_p$) y el número de resortes en serie ($N_s$) con el largo del resorte microscópico ($l$) y la sección del resorte microscópico ($s$).
Con estos valores, se puede calcular la constante de resorte de toda una secci n multiplicando por el número de resortes en paralelo ($N_p$) con la constante de Hook microscópica ($k_m$). De esta manera, se puede calcular la constante de Hooke ($k$) dividiendo el valor obtenido por el número de resortes en serie ($N_s$):
$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$
Si se introducen las expresiones para el n mero de elementos con el largo del resorte microscópico ($l$) y la sección del resorte microscópico ($s$), se obtiene la siguiente expresi n:
La expresi n para la constante de Hooke ($k$) dada por
posee dos par metros macrosc picos, que son el largo del cuerpo ($L$) y la sección del elemento ($S$). Los dem s, la constante de Hook microscópica ($k_m$), el largo del resorte microscópico ($l$) y la sección del resorte microscópico ($s$), son microsc picos y dependen del material que se describe. Por lo tanto, tiene sentido definir estos factores como el módulo de Elasticidad ($E$), de modo que:
Ya que la Ley de Hooke relaciona la fuerza elástica ($F_k$) a trav s de la constante de Hooke ($k$) y la elongación ($u$) de la manera siguiente:
es posible sustituir la constante de Hooke ($k$) por la expresi n microsc pica y utilizando la definici n de el módulo de Elasticidad ($E$), se obtiene con el largo del cuerpo ($L$) y la sección del elemento ($S$) que:
ID:(1884, 0)