Pendule physique
Description 
Dans le cas d'un pendule composé avec une masse réelle, l'énergie potentielle est générée par l'élévation du centre de masse contre le champ gravitationnel à mesure que le pendule se dévie d'un angle donné.
Variables
Calculs
Calculs
Équations
A écart de travail ($\Delta W$) nécessaire pour quun objet passe de a vitesse angulaire initiale ($\omega_0$) à A vitesse angulaire ($\omega$) est obtenue en appliquant un a torque ($T$) qui produit un déplacement angulaire a différence d'angles ($\Delta\theta$), selon :
| $ \Delta W = T \Delta\theta $ |
En appliquant la deuxième loi de Newton pour la rotation, avec a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et a accélération angulaire moyenne ($\bar{\alpha}$) :
| $ T = I \alpha $ |
cette expression peut être réécrite comme :
$\Delta W = I \alpha \Delta\theta$
ou, en utilisant a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) :
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
nous obtenons :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
En utilisant la définition de a vitesse angulaire moyenne ($\bar{\omega}$) et le temps écoulé ($\Delta t$) :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
il en résulte :
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
où A différence de vitesses angulaires ($\Delta\omega$) sexprime comme :
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Dautre part, la vitesse angulaire peut être approximée par la vitesse angulaire moyenne :
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
En combinant les deux expressions, on obtient léquation :
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Ainsi, la variation dénergie sexprime comme :
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Cela permet de définir lénergie cinétique de rotation comme :
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3687)
L' nergie potentielle gravitationnelle d'un pendule avec une masse
| $ U = m g L (1-\cos \theta )$ |
o
Pour de petits angles, la fonction cosinus peut tre approxim e par le d veloppement en s rie de Taylor jusqu' l'ordre deux
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
Cette approximation conduit une simplification de l' nergie potentielle en
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
(ID 4514)
Étant donné que a énergie cinétique de rotation ($K_r$) du pendule physique, en fonction de a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et de a vitesse angulaire ($\omega$), est représenté par :
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
et que a énergie potentielle du pendule ($V$), en fonction de a masse gravitationnelle ($m_g$), a longueur du pendule ($L$), a angle d'oscillation ($\theta$) et a accélération gravitationnelle ($g$), sexprime comme :
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
Léquation de lénergie totale sécrit :
$E = \displaystyle\frac{1}{2}I\omega^2 + \displaystyle\frac{1}{2}mgl\theta^2$
Sachant que a période ($T$) est défini comme :
$T = 2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
Nous pouvons déterminer la fréquence angulaire comme suit :
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
(ID 12338)
En utilisant le nombre complexe
introduit dans
nous obtenons
$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$
ainsi, la vitesse est obtenue comme la partie r elle
(ID 14076)
Exemples
(ID 15850)
Contrairement au pendule mathématique, le pendule physique prend en compte une a masse gravitationnelle ($m_g$) étendue au lieu dune masse ponctuelle. Bien que a longueur du pendule ($L$) soit défini comme la distance entre laxe de rotation et le centre de masse du corps ce qui rend lénergie potentielle équivalente dans les deux modèles , a énergie cinétique de rotation ($K_r$) ne peut plus être approximé à laide dexpressions qui dépendent uniquement de a longueur du pendule ($L$) et de a masse gravitationnelle ($m_g$). Dans ce cas, il est essentiel de connaître le a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) réel du corps pour représenter correctement son comportement dynamique.
(ID 7097)
Contrairement au pendule mathématique, le pendule physique prend en compte une a masse gravitationnelle ($m_g$) étendue au lieu dune masse ponctuelle. En définissant a longueur du pendule ($L$) comme la distance entre laxe de rotation et le centre de masse du corps, a énergie potentielle du pendule ($V$) est identique dans les deux modèles. Cependant, a énergie cinétique de rotation ($K_r$) ne peut plus être approximée par lexpression qui dépend uniquement de a longueur du pendule ($L$) et de a masse gravitationnelle ($m_g$) ; il est nécessaire dintégrer a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) du corps pour représenter correctement la distribution de masse.
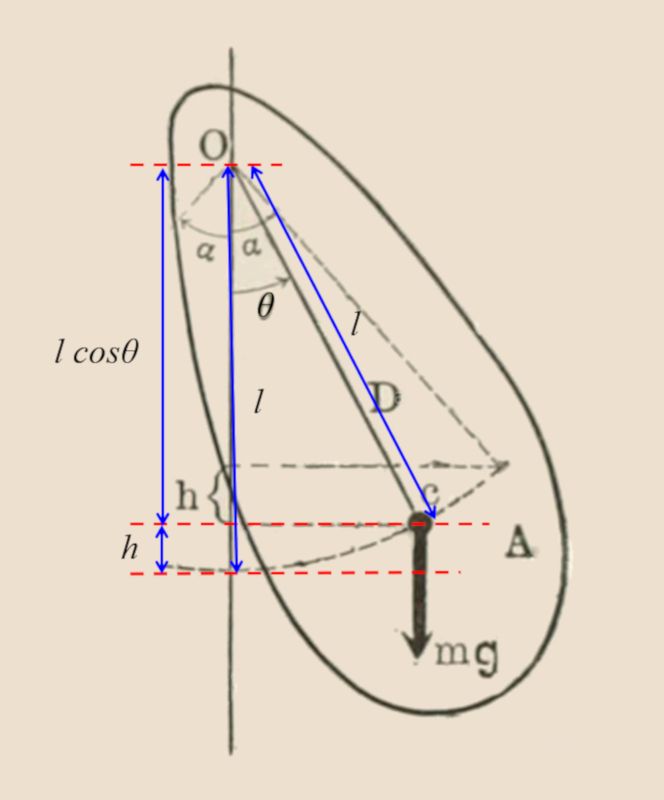
(ID 1188)
(ID 15853)
A énergie totale ($E$) correspond à la somme de a énergie cinétique totale ($K$) et a énergie potentielle ($V$) :
| $ E = K + V $ |
(ID 3687)
A énergie cinétique de rotation ($K_r$) est une fonction de a vitesse angulaire ($\omega$) et dune mesure de linertie représentée par a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) :
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
L' nergie potentielle gravitationnelle d'un pendule est
| $ U = m g L (1-\cos \theta )$ |
qui peut tre approxim e pour de petits angles comme :
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
Il est important de noter que l'angle doit tre en radians.
(ID 4514)
A fréquence angulaire du pendule physique ($\omega_0$) est déterminé en fonction de a masse gravitationnelle ($m_g$), a longueur du pendule ($L$), a moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) et a accélération gravitationnelle ($g$) :
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
La relation entre a fréquence angulaire ($\omega$) et a fréquence du son ($\nu$) sexprime comme :
| $ \omega = 2 \pi \nu $ |
(ID 12338)
A fréquence angulaire ($\omega$) est avec a période ($T$) gal
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
(ID 12335)
A fréquence du son ($\nu$) correspond au nombre de fois qu'une oscillation se produit en une seconde. A période ($T$) repr sente le temps n cessaire une seule oscillation. Par cons quent, le nombre d'oscillations par seconde est :
| $ \nu =\displaystyle\frac{1}{ T }$ |
La fr quence est indiqu e en Hertz (Hz).
(ID 4427)
Avec la description de l'oscillation l'aide de
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
la partie r elle correspond l' volution temporelle de l'amplitude
| $ x = x_0 \cos \omega_0 t $ |
(ID 14074)
En obtenant la partie r elle de la d riv e du nombre complexe repr sentant l'oscillation
dont la partie r elle correspond la vitesse
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
ID:(1421, 0)
