Steiner's Theorem
Storyboard 
In general, moments of inertia are calculated with respect to axes that pass through the center of mass. However, in many situations rotation occurs around another axis. In that case, the moment of inertia on the throne of any parallel axis can be calculated based on the Steiner theorem, for which only the moment of inertia is needed with respect to the center of mass, the mass and the distance between the real axis and the one passes through the center of mass.
ID:(1456, 0)
Application of Steiner's theorem for a cylinder, $\parallel$ axis
Definition 
For a cylinder with an axis parallel to the cylinder's own axis:
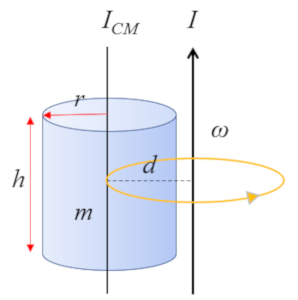
whose moment of inertia about the center of mass (CM) is given by
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
the moment of inertia can be calculated using the Steiner's theorem with the following formula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11551, 0)
Application of Steiner's theorem for a cylinder, $\perp$ axis
Image 
For a cylinder with an axis perpendicular to the cylinder's own axis:
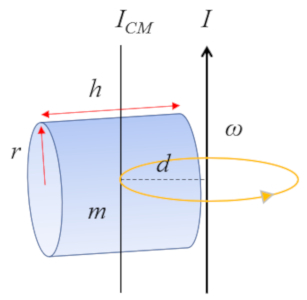
whose moment of inertia about the center of mass (CM) is defined as
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11552, 0)
Application of Steiner's theorem for a right parallelepiped
Note 
For a right parallelepiped with an axis parallel to an edge:
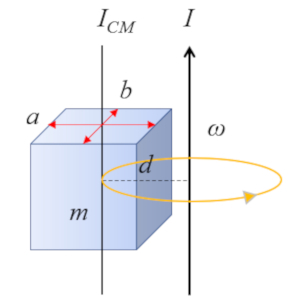
whose moment of inertia about the center of mass (CM) is defined as
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11554, 0)
Application of Steiner's theorem to a sphere
Quote 
For a sphere with an axis at a distance from its center:

whose moment of inertia about the center of mass (CM) is defined as
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11553, 0)
Steiner's Theorem
Storyboard 
In general, moments of inertia are calculated with respect to axes that pass through the center of mass. However, in many situations rotation occurs around another axis. In that case, the moment of inertia on the throne of any parallel axis can be calculated based on the Steiner theorem, for which only the moment of inertia is needed with respect to the center of mass, the mass and the distance between the real axis and the one passes through the center of mass.
Variables
Calculations
Calculations
Equations
Examples
The moment of inertia for axis that does not pass through the CM ($I$) can be calculated using the moment of Inertia Mass Center ($I_{CM}$) and adding the moment of inertia of the body mass ($m$) as if it were a point mass at the distance Center of Mass and Axis ($d$):
For a cylinder with an axis parallel to the cylinder's own axis:
whose moment of inertia about the center of mass (CM) is given by
the moment of inertia can be calculated using the Steiner's theorem with the following formula
For a cylinder with an axis perpendicular to the cylinder's own axis:
whose moment of inertia about the center of mass (CM) is defined as
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
For a right parallelepiped with an axis parallel to an edge:
whose moment of inertia about the center of mass (CM) is defined as
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
For a sphere with an axis at a distance from its center:
whose moment of inertia about the center of mass (CM) is defined as
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula
ID:(1456, 0)
