Benützer:


Steiners Satz
Storyboard

Im Allgemeinen werden Trägheitsmomente in Bezug auf Achsen berechnet, die durch den Schwerpunkt verlaufen. In vielen Situationen tritt jedoch eine Drehung um eine andere Achse auf. In diesem Fall kann das Trägheitsmoment auf dem Thron einer beliebigen parallelen Achse auf der Grundlage des Steiner-Theorems berechnet werden, für das nur das Trägheitsmoment in Bezug auf den Massenmittelpunkt, die Masse und den Abstand zwischen der realen Achse und der einen Achse benötigt wird geht durch den Schwerpunkt.

>Modell

ID:(1456, 0)


Steiners Satz
Beschreibung

Im Allgemeinen werden Trägheitsmomente in Bezug auf Achsen berechnet, die durch den Schwerpunkt verlaufen. In vielen Situationen tritt jedoch eine Drehung um eine andere Achse auf. In diesem Fall kann das Trägheitsmoment auf dem Thron einer beliebigen parallelen Achse auf der Grundlage des Steiner-Theorems berechnet werden, für das nur das Trägheitsmoment in Bezug auf den Massenmittelpunkt, die Masse und den Abstand zwischen der realen Achse und der einen Achse benötigt wird geht durch den Schwerpunkt.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$d$
d
Entfernung Schwerpunkt und Achse
m
$m$
m
Körpermasse
kg
$I$
I
Trägheitsmoment für Achse, die nicht durch das CM verläuft
kg m^2
$I_{CM}$
I_CM
Trägheitsmoment Massenzentrum
kg m^2

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

F r einen Zylinder mit einer Achse, die parallel zur Zylinderachse verl uft:



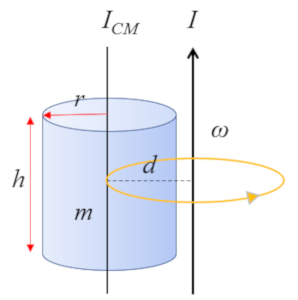
dessen Tr gheitsmoment bez glich des Schwerpunkts (CM) wie folgt definiert ist:

$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$



kann das Tr gheitsmoment mithilfe des Steiner'schen Satzes mit folgender Formel berechnet werden: entfernung Schwerpunkt und Achse $m$, körpermasse $kg$, trägheitsmoment für Achse, die nicht durch das CM verläuft $kg m^2$ und trägheitsmoment Massenzentrum $kg m^2$

$ I = I_{CM} + m d ^2$

.

(ID 11551)

F r einen Zylinder mit einer Achse, die senkrecht zur Zylinderachse verl uft:



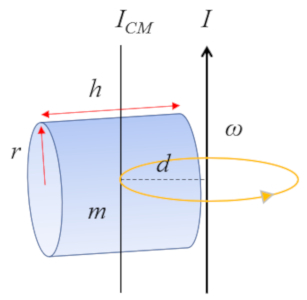
dessen Tr gheitsmoment bez glich des Schwerpunkts (CM) wie folgt definiert ist:

$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$



kann das Tr gheitsmoment mithilfe des Steiner'schen Satzes mit folgender Formel berechnet werden:

$ I = I_{CM} + m d ^2$

.

(ID 11552)

F r ein rechtwinkliges Parallelepiped mit einer Achse parallel zu einer Kante:



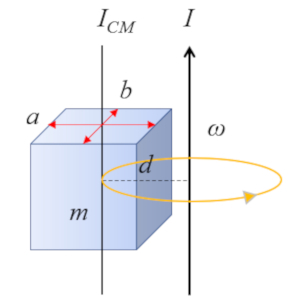
dessen Tr gheitsmoment bez glich des Schwerpunkts (CM) wie folgt definiert ist:

$ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$



kann das Tr gheitsmoment mithilfe des Steiner'schen Satzes mit folgender Formel berechnet werden:

$ I = I_{CM} + m d ^2$

.

(ID 11554)

F r eine Kugel mit einer Achse in einer gewissen Entfernung von ihrem Zentrum:



dessen Tr gheitsmoment bez glich des Schwerpunkts (CM) wie folgt definiert ist:

$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$



kann das Tr gheitsmoment mithilfe des Steiner'schen Satzes mit folgender Formel berechnet werden: entfernung Schwerpunkt und Achse $m$, körpermasse $kg$, trägheitsmoment für Achse, die nicht durch das CM verläuft $kg m^2$ und trägheitsmoment Massenzentrum $kg m^2$

$ I = I_{CM} + m d ^2$

.

(ID 11553)

ID:(1456, 0)