Utilisateur:
Théorème de Steiner
Description 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Exemples
Pour un cylindre avec un axe parall le son propre axe :
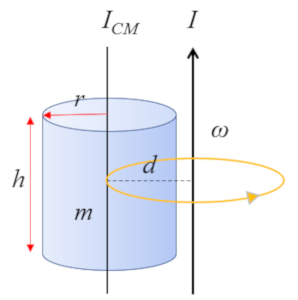
dont le moment d'inertie par rapport au centre de masse (CM) est donn par
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
le moment d'inertie peut tre calcul en utilisant le th or me de Steiner avec la formule suivante
| $ I = I_{CM} + m d ^2$ |
.
(ID 11551)
Pour un cylindre avec un axe perpendiculaire son propre axe :
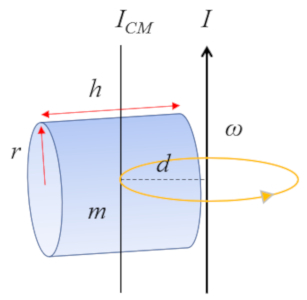
dont le moment d'inertie par rapport au centre de masse (CM) est d fini comme
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
le calcul du moment d'inertie peut tre effectu en utilisant le th or me de Steiner avec la formule suivante
| $ I = I_{CM} + m d ^2$ |
.
(ID 11552)
Pour un parall l pip de rectangle d'axe parall le une ar te:
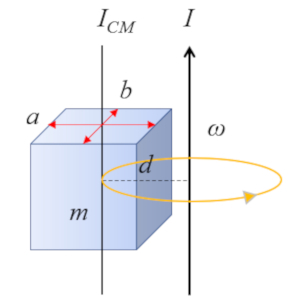
dont le moment d'inertie par rapport au centre de masse (CM) est d fini comme
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
le calcul du moment d'inertie peut tre effectu en utilisant le th or me de Steiner avec la formule suivante
| $ I = I_{CM} + m d ^2$ |
.
(ID 11554)
Pour une sph re avec un axe une distance de son centre :
dont le moment d'inertie par rapport au centre de masse (CM) est d fini comme
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
le calcul du moment d'inertie peut tre effectu en utilisant le th or me de Steiner avec la formule suivante distance centre de masse et axe $m$, masse corporelle $kg$, moment d\'inertie de l\'axe qui ne passe pas par le CM $kg m^2$ et moment d\'inertie du centre de masse $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
(ID 11553)
ID:(1456, 0)