Moment of inertia
Storyboard 
The moment of inertia is the rotating factor that is equivalent to the mass in the translation.The moment of inertia can be determined empirically by rotating a body around an axis or calculating how the mass is distributed around the axis.
ID:(600, 0)
Bar that rotates around an axis $\perp$
Image 
A bar with mass $m$ and length $l$ rotating around its center, which coincides with the center of mass:
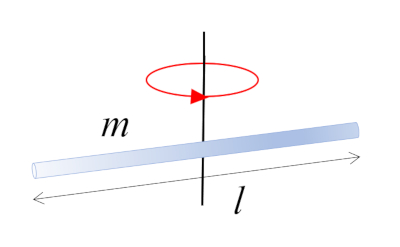
ID:(10962, 0)
Cylinder rotating around axis $\parallel$
Image 
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
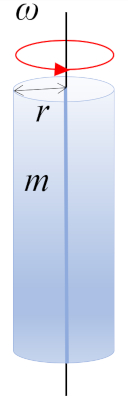
ID:(10964, 0)
Cylinder that rotates about axis $\perp$
Image 
In this scenario, a cylinder with mass $m$, radius $r$, and height $h$ is rotating around an axis perpendicular to its own axis. This axis passes through the midpoint of the cylinder's length, where the center of mass (CM) is located:
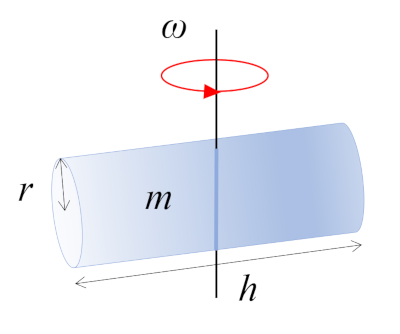
ID:(10965, 0)
Regular parallelepiped moment of inertia
Image 
A straight rectangular parallelepiped with mass $m$ and sides $a$ and $b$, perpendicular to the axis of rotation, is rotating around its center of mass, which is located at the geometric center of the body:
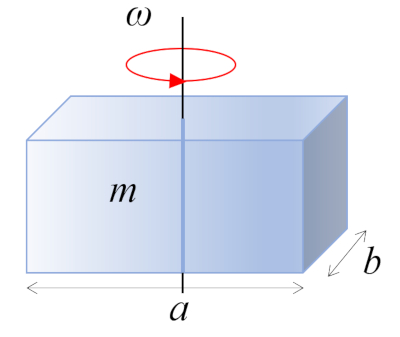
ID:(10973, 0)
Straight parallelepiped
Image 
In the case of a right rectangular parallelepiped with mass $m$ and side $a$, the center of mass is located at the geometric center:
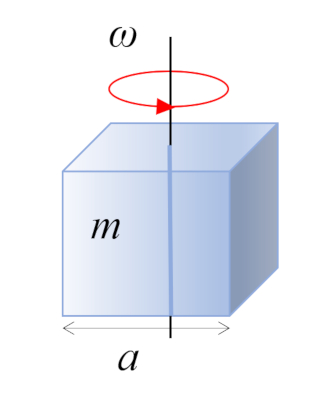
ID:(10963, 0)
Sphere
Image 
A sphere with mass $m$ and radius $r$ is rotating around its center of mass, which is located at its geometric center:
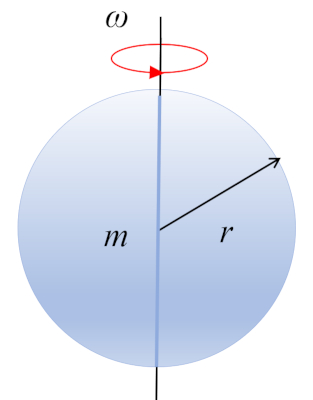
ID:(10490, 0)
