Força viscosa
Storyboard 
A força viscosa geralmente é modelada como sendo proporcional à velocidade do objeto. A constante da força viscosa é proporcional à viscosidade do meio e a fatores relacionados à geometria do objeto.Se nenhuma outra força estiver atuando, a força viscosa tende a desacelerar um objeto que está inicialmente se movendo com uma velocidade dada.
ID:(1415, 0)
Força viscosa sobre um corpo
Conceito 
A força experimentada por um corpo que se desloca com uma velocidade de ERROR:6029.1 em um meio, caracterizado por la constante de força viscosa ($b$), é La força viscosa ($F_v$), como descrito pela equação:
| $ F_v = b v $ |
Para entender o papel de la constante de força viscosa ($b$), é importante lembrar que a viscosidade é uma medida de como o momento, ou a velocidade das moléculas, se difunde. Em outras palavras, la constante de força viscosa ($b$) é a medida pela qual o corpo perde energia ao transferi-la para o meio e ao acelerar as moléculas, fornecendo-lhes energia. Portanto, la constante de força viscosa ($b$) é proporcional à viscosidade.
ID:(15546, 0)
Método Ostwald para medir a viscosidade
Descrição 
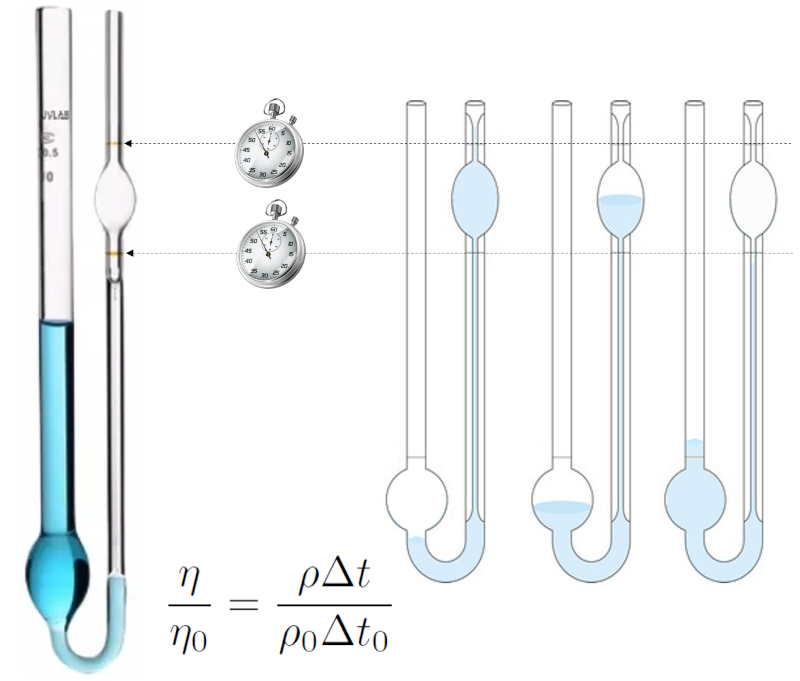
O método de medição de viscosidade de Ostwald baseia-se no comportamento de um líquido fluindo através de um tubo de pequeno raio (capilar).
O líquido é introduzido, aplica-se sucção para exceder a marca superior e, em seguida, permite-se que escorra, medindo o tempo que leva para o nível passar da marca superior para a inferior.
O experimento é conduzido primeiro com um líquido para o qual a viscosidade e a densidade são conhecidas (por exemplo, água destilada), e depois com o líquido para o qual se deseja determinar a viscosidade. Se as condições forem idênticas, o líquido fluindo em ambos os casos será semelhante e, assim, o tempo será proporcional à densidade dividida pela viscosidade. Portanto, pode-se estabelecer uma equação de comparação entre ambas as viscosidades:
ID:(15545, 0)
Velocidade em meio viscoso
Conceito 
No caso de um corpo caindo em um meio viscoso, a equação de movimento é uma equação de la velocidade ($v$) em função de o tempo ($t$) com la massa inercial ($m_i$) e la constante de força viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Isso é obtido com la tempo de viscosidade e massa inercial ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
Integrando com tempo inicial zero e la velocidade inicial ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
que é representado abaixo:
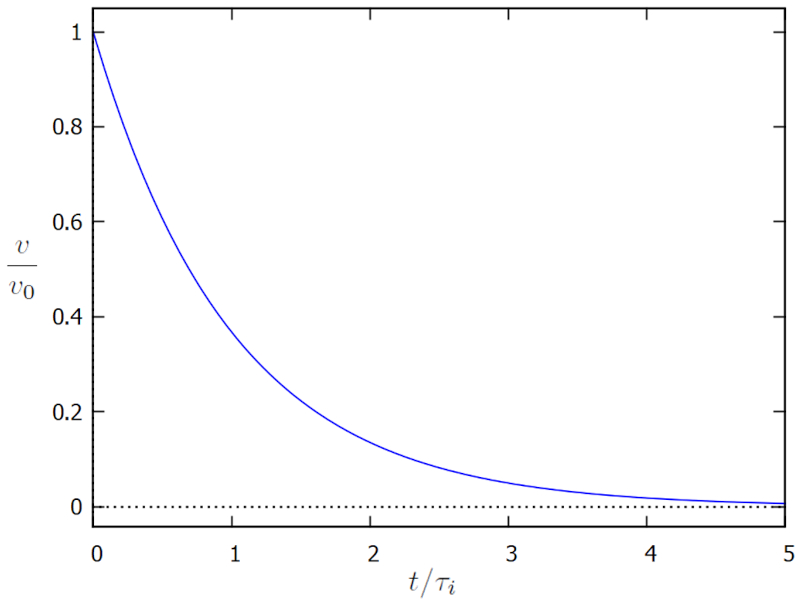
O gráfico ilustra como a viscosidade força o corpo a descer até zero, o que ocorre aproximadamente em um tempo da ordem de la tempo de viscosidade e massa inercial ($\tau_i$).
ID:(15552, 0)
Trajetória em meio viscoso
Conceito 
No caso de um corpo caindo em um meio viscoso, a equação de movimento é uma equação de la posição ($s$) em função de la velocidade inicial ($v_0$), la tempo de viscosidade e massa inercial ($\tau_i$) e o tempo ($t$):
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
A partir desta equação, obtemos integrando com tempo inicial zero e uma velocidade ($s_0$):
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
que é representada abaixo:
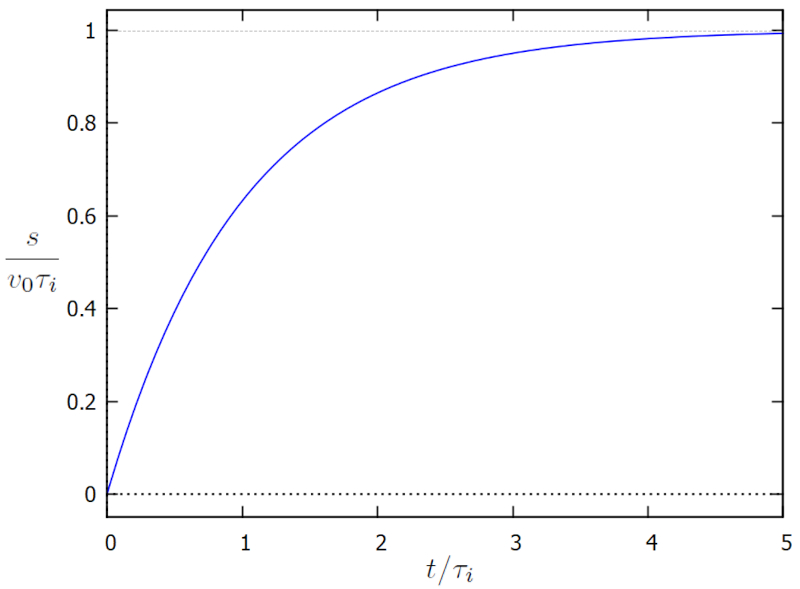
ID:(15551, 0)
Força viscosa
Descrição 
A força viscosa geralmente é modelada como sendo proporcional à velocidade do objeto. A constante da força viscosa é proporcional à viscosidade do meio e a fatores relacionados à geometria do objeto. Se nenhuma outra força estiver atuando, a força viscosa tende a desacelerar um objeto que está inicialmente se movendo com uma velocidade dada.
Variáveis
Cálculos
Cálculos
Equações
(ID 3243)
Dado que o momento ($p$) se define con la massa inercial ($m_i$) y la velocidade ($v$),
| $ p = m_i v $ |
Si la massa inercial ($m_i$) igual a la massa inicial ($m_0$), ent o podemos derivar o momento em rela o ao tempo e obter la força com massa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Portanto, chegamos conclus o de que
| $ F = m_i a $ |
(ID 10975)
Dado que a for a total la força com massa constante ($F$) igual a menos la força viscosa ($F_v$):
e la força com massa constante ($F$) composta por la massa inercial ($m_i$) e la aceleração instantânea ($a$):
| $ F = m_i a $ |
e la força viscosa ($F_v$) composta por la constante de força viscosa ($b$) e la velocidade ($v$):
| $ F_v = b v $ |
obtemos
| $ m_i a = - b v $ |
(ID 14498)
Com la velocidade ($v$), o tempo ($t$), la massa inercial ($m_i$) e la constante de força viscosa ($b$), temos a equa o:
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
que, com la tempo de viscosidade e massa inercial ($\tau_i$) definido por
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
pode ser reescrita como
$\displaystyle\frac{dv}{dt}=-\displaystyle\frac{v}{\tau_i}$
cuja solu o
| $ v = v_0 e^{- t / \tau_i }$ |
(ID 14500)
(ID 15553)
Exemplos
(ID 15522)
A for a experimentada por um corpo que se desloca com uma velocidade de ERROR:6029.1 em um meio, caracterizado por la constante de força viscosa ($b$), la força viscosa ($F_v$), como descrito pela equa o:
| $ F_v = b v $ |
Para entender o papel de la constante de força viscosa ($b$), importante lembrar que a viscosidade uma medida de como o momento, ou a velocidade das mol culas, se difunde. Em outras palavras, la constante de força viscosa ($b$) a medida pela qual o corpo perde energia ao transferi-la para o meio e ao acelerar as mol culas, fornecendo-lhes energia. Portanto, la constante de força viscosa ($b$) proporcional viscosidade.
(ID 15546)
O m todo de medi o de viscosidade de Ostwald baseia-se no comportamento de um l quido fluindo atrav s de um tubo de pequeno raio (capilar).
O l quido introduzido, aplica-se suc o para exceder a marca superior e, em seguida, permite-se que escorra, medindo o tempo que leva para o n vel passar da marca superior para a inferior.
O experimento conduzido primeiro com um l quido para o qual a viscosidade e a densidade s o conhecidas (por exemplo, gua destilada), e depois com o l quido para o qual se deseja determinar a viscosidade. Se as condi es forem id nticas, o l quido fluindo em ambos os casos ser semelhante e, assim, o tempo ser proporcional densidade dividida pela viscosidade. Portanto, pode-se estabelecer uma equa o de compara o entre ambas as viscosidades:

(ID 15545)
No caso de um corpo caindo em um meio viscoso, a equa o de movimento uma equa o de la velocidade ($v$) em fun o de o tempo ($t$) com la massa inercial ($m_i$) e la constante de força viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Isso obtido com la tempo de viscosidade e massa inercial ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
Integrando com tempo inicial zero e la velocidade inicial ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
que representado abaixo:

O gr fico ilustra como a viscosidade for a o corpo a descer at zero, o que ocorre aproximadamente em um tempo da ordem de la tempo de viscosidade e massa inercial ($\tau_i$).
(ID 15552)
No caso de um corpo caindo em um meio viscoso, a equa o de movimento uma equa o de la posição ($s$) em fun o de la velocidade inicial ($v_0$), la tempo de viscosidade e massa inercial ($\tau_i$) e o tempo ($t$):
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
A partir desta equa o, obtemos integrando com tempo inicial zero e uma velocidade ($s_0$):
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
que representada abaixo:

(ID 15551)
(ID 15534)
ID:(1415, 0)
