Storyboard

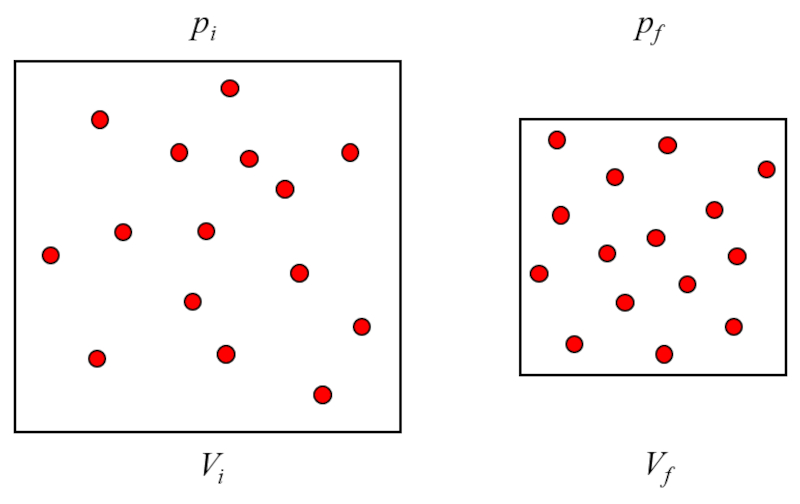
Das Gesetz von Boyle-Mariotte besagt, dass das Produkt von die Druck ($p$) und der Volumen ($V$) eines Gases konstant bleibt, wenn die absolute Temperatur und die Stoffmenge nicht variieren.

Das bedeutet, dass die Druck ($p$) umgekehrt proportional zu der Volumen ($V$) variiert.

>Modell

ID:(1472, 0)

Iframe

>Top

Das Boyle-Mariotte-Gesetz, auch einfach als Boyle'sches Gesetz bekannt, beschreibt die umgekehrte Beziehung zwischen dem Druck und dem Volumen eines Gases bei konstanter Temperatur. Es besagt, dass für eine feste Menge Gas, wenn die Temperatur konstant gehalten wird, der Druck des Gases steigt, wenn das Volumen abnimmt, und umgekehrt. Das bedeutet, dass wenn man ein Gas durch Reduzierung seines Volumens komprimiert, der Druck proportional zunimmt, und wenn man das Volumen vergrößert, der Druck proportional abnimmt. Diese Beziehung ist grundlegend für das Verständnis des Verhaltens von Gasen und wird mathematisch durch das Produkt von Druck und Volumen als eine Konstante für eine gegebene Gasmenge bei konstanter Temperatur ausgedrückt.

ID:(15254, 0)

Konzept

>Top

Die Druck ($p$) entsteht, wenn Gaspartikel mit der Oberfläche des Gasbehälters kollidieren. Da die Absolute Temperatur ($T$) konstant ist, variiert die Energie der Partikel nicht, und die Stöße dieser Partikel mit den Oberflächen des Gasbehälters werden sich im übertragenen Impuls nicht ändern. Die Anzahl der Stöße hängt jedoch von der Anzahl der Partikel in der Nähe der Oberfläche ab, was wiederum proportional zum die Partikelkonzentration ($c_n$) des Gases ist.

Auf der anderen Seite ist die Dichte umgekehrt proportional zu der Volumen ($V$), was zu folgender Beziehung führt:

$p \propto c_n \propto \displaystyle\frac{1}{V}$

ID:(9602, 0)

Beschreibung

>Top

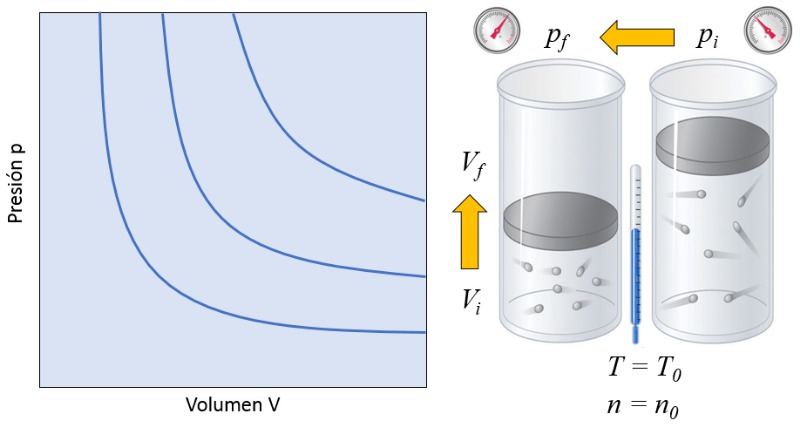
In einem Gas, wenn sowohl die Absolute Temperatur ($T$) als auch der Anzahl der Partikel ($N$) konstant gehalten werden, beobachtet man, dass der Volumen ($V$) und die Druck ($p$) sich invers proportional verhalten. Immer wenn der Volumen ($V$) reduziert wird, erhöht sich die Druck ($p$) und umgekehrt,

$p \propto \displaystyle\frac{1}{V}$

wie in der folgenden Grafik dargestellt:

Die Beziehung zwischen der Anzahl der Partikel ($N$) und die Absolute Temperatur ($T$) ist, dass ihr Produkt gleich eine Boyles Gesetzeskonstante ($C_b$) ist, was dem Boyle'schen Gesetz [1] entspricht, benannt nach seinem Entdecker Robert Boyle:

Manchmal sprechen wir über das Boyle-Mariotte-Gesetz und erinnern uns an den französischen Physiker Edme Mariotte, der das gleiche Gesetz 1676 unabhängig voneinander entdeckte.

[1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Neue physikalisch-mechanische Experimente, die den Federmechanismus der Luft und seine Auswirkungen betreffen), Robert Boyle, Oxford: gedruckt von H. Hall, Drucker der Universität, für Tho. Robinson (1660).

ID:(9531, 0)

Beschreibung

>Top

Robert Boyle war ein irischer Wissenschaftler, der 1627 geboren wurde. Er gilt als einer der Begründer der modernen Chemie und ist besonders für seine Beiträge zum Verhalten von Gasen bekannt. Die Beziehung zwischen Robert Boyle und dem Boyle'schen Gesetz besteht darin, dass er dieses Gesetz im 17. Jahrhundert formuliert hat. Das Boyle'sche Gesetz besagt, dass bei konstanter Temperatur das Volumen eines Gases umgekehrt proportional zum Druck ist. Boyle führte Experimente durch, die diese Beziehung nachwiesen und legte damit den Grundstein für das Verständnis des Gasverhaltens.

ID:(1657, 0)

Konzept

>Top

Das Boyle'sche Gesetz besagt, dass bei konstanter die Absolute Temperatur ($T$) das Produkt von die Druck ($p$) und der Volumen ($V$) gleich die Boyles Gesetzeskonstante ($C_b$) ist:

Das bedeutet, dass wenn ein Gas von einem Anfangszustand (die Druck im Ausgangszustand ($p_i$) und der Volumen im Zustand i ($V_i$)) in einen Endzustand (die Druck im Endzustand ($p_f$) und der Volumen im Zustand f ($V_f$)) übergeht und dabei die Absolute Temperatur ($T$) konstant bleibt, es immer das Boyle'sche Gesetz erfüllen muss:

$p_i V_i = C_b = p_f V_f$

Daher ergibt sich:

ID:(15688, 0)

Konzept

>Top

Wenn bei einer isothermen Änderung, bei der sich der Inhalt nicht ändert, die Druck im Ausgangszustand ($p_i$), die Druck im Endzustand ($p_f$), der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$) durch folgende Gleichung in Beziehung stehen:

Dann kann die Dichte ($\rho$) eingeführt werden, das zusammen mit die Masse ($M$) und der Volumen ($V$) folgende Bedingung erfüllt:

Dies führt uns zu die Dichte im Zustand i ($\rho_i$) und die Dichte im Zustand f ($\rho_f$) als:

ID:(15687, 0)

Top

>Top

Parameter

$C_b$

C_b

Boyles Gesetzeskonstante

J

$M$

M

Masse

kg

Variablen

$\rho_f$

rho_f

Dichte im Zustand f

kg/m^3

$\rho_i$

rho_i

Dichte im Zustand i

kg/m^3

$p_i$

p_i

Druck im Ausgangszustand

Pa

$p_f$

p_f

Druck im Endzustand

Pa

$V_f$

V_f

Volumen im Zustand f

m^3

$V_i$

V_i

Volumen im Zustand i

m^3

Berechnungen

• Alternative Methode
• Traditionelle Methode
• Strategie
• 2D
• 3D

Gleichung

Zahl

Zuerst die Gleichung auswählen: zu , dann die Variable auswählen: zu

---

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable Gegeben Berechnen Ziel : Gleichung Zu verwenden

Gleichungen

ID:(15313, 0)

Gleichung

>Top, >Modell

Das Boyle'sche Gesetz stellt eine Beziehung zwischen der Volumen ($V$) und die Druck ($p$) her und besagt, dass ihr Produkt gleich die Boyles Gesetzeskonstante ($C_b$) ist, wie folgt:

$ p_i V_i = C_b $

$ p V = C_b $

Bedingungen

Variablen

$C_b$

Boyles Gesetzeskonstante

$J$

9335

$p$

$p_i$

Druck im Ausgangszustand

$Pa$

5232

$V$

$V_i$

Volumen im Zustand i

$m^3$

5234

Beziehung

ID:(582, 1)

Gleichung

>Top, >Modell

Das Boyle'sche Gesetz stellt eine Beziehung zwischen der Volumen ($V$) und die Druck ($p$) her und besagt, dass ihr Produkt gleich die Boyles Gesetzeskonstante ($C_b$) ist, wie folgt:

$ p_f V_f = C_b $

$ p V = C_b $

Bedingungen

Variablen

$C_b$

Boyles Gesetzeskonstante

$J$

9335

$p$

$p_f$

Druck im Endzustand

$Pa$

5233

$V$

$V_f$

Volumen im Zustand f

$m^3$

5235

Beziehung

ID:(582, 2)

Gleichung

>Top, >Modell

Wenn ein Gas von einem Anfangszustand (i) in einen Endzustand (f) übergeht und die Absolute Temperatur ($T$) konstant bleibt, gilt für die Druck im Ausgangszustand ($p_i$), die Druck im Endzustand ($p_f$), der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$):

$ p_i V_i = p_f V_f $

Bedingungen

Variablen

$p_i$

Druck im Ausgangszustand

$Pa$

5232

$p_f$

Druck im Endzustand

$Pa$

5233

$V_f$

Volumen im Zustand f

$m^3$

5235

$V_i$

Volumen im Zustand i

$m^3$

5234

Beziehung

Entwicklung

Das Boyle'sche Gesetz besagt, dass bei konstanter die Absolute Temperatur ($T$) das Produkt von die Druck ($p$) und der Volumen ($V$) gleich die Boyles Gesetzeskonstante ($C_b$) ist:

$ p V = C_b $

Das bedeutet, dass wenn ein Gas von einem Anfangszustand (die Druck im Ausgangszustand ($p_i$) und der Volumen im Zustand i ($V_i$)) in einen Endzustand (die Druck im Endzustand ($p_f$) und der Volumen im Zustand f ($V_f$)) übergeht und dabei die Absolute Temperatur ($T$) konstant bleibt, es immer das Boyle'sche Gesetz erfüllen muss:

$p_i V_i = C_b = p_f V_f$

Daher ergibt sich:

$ p_i V_i = p_f V_f $

ID:(3491, 0)

Gleichung

>Top, >Modell

Die Dichte ($\rho$) wird als das Verhältnis zwischen die Masse ($M$) und der Volumen ($V$) definiert, ausgedrückt als:

$ \rho_i \equiv\displaystyle\frac{ M }{ V_i }$

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Bedingungen

Variablen

$\rho$

$\rho_i$

Dichte im Zustand i

$kg/m^3$

7833

$M$

Masse

$kg$

5183

$V$

$V_i$

Volumen im Zustand i

$m^3$

5234

Beziehung

Diese Eigenschaft ist spezifisch für das betreffende Material.

ID:(3704, 1)

Gleichung

>Top, >Modell

Die Dichte ($\rho$) wird als das Verhältnis zwischen die Masse ($M$) und der Volumen ($V$) definiert, ausgedrückt als:

$ \rho_f \equiv\displaystyle\frac{ M }{ V_f }$

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Bedingungen

Variablen

$\rho$

$\rho_f$

Dichte im Zustand f

$kg/m^3$

7834

$M$

Masse

$kg$

5183

$V$

$V_f$

Volumen im Zustand f

$m^3$

5235

Beziehung

Diese Eigenschaft ist spezifisch für das betreffende Material.

ID:(3704, 2)

Gleichung

>Top, >Modell

Das Boyle'sche Gesetz für den Anfangszustand (die Dichte im Zustand i ($\rho_i$), die Druck im Ausgangszustand ($p_i$)) und den Endzustand (die Dichte im Zustand f ($\rho_f$), die Druck im Endzustand ($p_f$)) lautet:

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

Bedingungen

Variablen

$\rho_f$

Dichte im Zustand f

$kg/m^3$

7834

$\rho_i$

Dichte im Zustand i

$kg/m^3$

7833

$p_i$

Druck im Ausgangszustand

$Pa$

5232

$p_f$

Druck im Endzustand

$Pa$

5233

Beziehung

Entwicklung

Wenn bei einer isothermen Änderung, bei der sich der Inhalt nicht ändert, die Druck im Ausgangszustand ($p_i$), die Druck im Endzustand ($p_f$), der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$) durch folgende Gleichung in Beziehung stehen:

$ p_i V_i = p_f V_f $

Dann kann die Dichte ($\rho$) eingeführt werden, das zusammen mit die Masse ($M$) und der Volumen ($V$) folgende Bedingung erfüllt:

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Dies führt uns zu die Dichte im Zustand i ($\rho_i$) und die Dichte im Zustand f ($\rho_f$) als:

$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$

ID:(8834, 0)