Utilizador:
Lei de Boyle-Mariotte
Storyboard 
A lei de Boyle-Mariotte estabelece que o produto de la pressão ($p$) e o volume ($V$) de um gás se mantém constante quando a temperatura absoluta e a quantidade de matéria não variam.
Isso significa que la pressão ($p$) varia inversamente proporcional a o volume ($V$).
ID:(1472, 0)
Mecanismos
Iframe
A lei de Boyle-Mariotte, também conhecida simplesmente como lei de Boyle, descreve a relação inversa entre a pressão e o volume de um gás a temperatura constante. Ela afirma que, para uma quantidade fixa de gás, quando a temperatura é mantida constante, a pressão do gás aumenta à medida que o volume diminui, e vice-versa. Isso significa que, se você comprimir um gás reduzindo seu volume, a pressão aumentará proporcionalmente, e se você expandir o volume, a pressão diminuirá proporcionalmente. Essa relação é fundamental para entender o comportamento dos gases e é expressa matematicamente pelo produto da pressão e do volume sendo uma constante para uma quantidade de gás dada a temperatura constante.
Mecanismos
ID:(15254, 0)
Variação de volume e pressão
Conceito
La pressão ($p$) é gerada quando as partículas de gás colidem com a superfície do recipiente de gás. Como la temperatura absoluta ($T$) é constante, a energia das partículas não varia e os impactos delas com as superfícies do recipiente de gás não variarão no impulso transferido. No entanto, o número de impactos depende do número de partículas próximas à superfície, que por sua vez é proporcional ao la concentração de partículas ($c_n$) do gás.
Por outro lado, a densidade é inversamente proporcional a o volume ($V$), resultando na seguinte relação:
$p \propto c_n \propto \displaystyle\frac{1}{V}$
ID:(9602, 0)
Relação volume e pressão
Descrição
Em um gás, se tanto la temperatura absoluta ($T$) quanto o número de partículas ($N$) forem mantidos constantes, observa-se que o volume ($V$) e la pressão ($p$) variam de forma inversamente proporcional. Sempre que o volume ($V$) é reduzido, la pressão ($p$) aumenta, e vice-versa,
$p \propto \displaystyle\frac{1}{V}$
como ilustrado no gráfico a seguir:
A relação entre o número de partículas ($N$) e la temperatura absoluta ($T$) é que seu produto é igual a uma constante da lei de Boyle ($C_b$), o que corresponde à lei de Boyle [1], em homenagem ao seu descobridor Robert Boyle:
| $ p V = C_b $ |
Às vezes falamos da lei Boyle-Mariotte, lembrando o físico francês Edme Mariotte que descobriu a mesma lei de forma independente em 1676.
[1] "New Experiments Physico-Mechanical, Touching the Spring of the Air, and Its Effects" (Novos experimentos físico-mecânicos, tocando a mola do ar e seus efeitos), Robert Boyle, Oxford: impresso por H. Hall, Printer to the University, para Tho. Robinson (1660).
ID:(9531, 0)
Robert Boyle
Descrição
Robert Boyle foi um cientista irlandês nascido em 1627. Ele é considerado um dos fundadores da química moderna e é conhecido por suas contribuições no campo do comportamento dos gases. A relação entre Robert Boyle e a Lei de Boyle se deve ao fato de que ele formulou essa lei no século XVII. A Lei de Boyle estabelece que, à temperatura constante, o volume de um gás é inversamente proporcional à sua pressão. Boyle realizou experimentos que comprovaram essa relação e lançaram as bases para a compreensão do comportamento dos gases.
ID:(1657, 0)
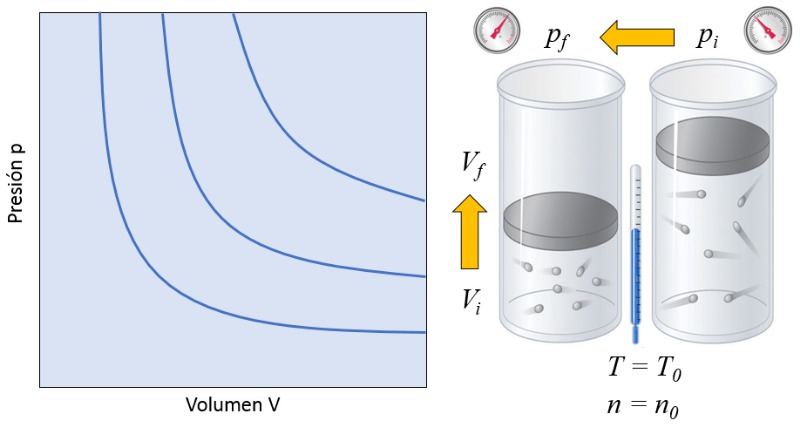
Mudança de estado de um gás ideal de acordo com a lei de Boyle
Conceito
A lei de Boyle estabelece que, com la temperatura absoluta ($T$) constante, o produto de la pressão ($p$) e o volume ($V$) é igual a la constante da lei de Boyle ($C_b$):
| $ p V = C_b $ |
Isso significa que, se um gás passar de um estado inicial (la pressão no estado inicial ($p_i$) e o volume no estado i ($V_i$)) para um estado final (la pressão em estado final ($p_f$) e o volume no estado f ($V_f$)), mantendo la temperatura absoluta ($T$) constante, ele deve sempre cumprir a lei de Boyle:
$p_i V_i = C_b = p_f V_f$
Portanto, tem-se que:
| $ p_i V_i = p_f V_f $ |
ID:(15688, 0)
Equivalente à lei de Boyle para densidades
Conceito
Se, em uma mudança isotérmica em que o conteúdo não varia, la pressão no estado inicial ($p_i$), la pressão em estado final ($p_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$) estão relacionados por:
| $ p_i V_i = p_f V_f $ |
Então, podemos introduzir la densidade ($\rho$), que, junto com la massa ($M$) e o volume ($V$), satisfaz:
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
O que nos leva a la densidade no estado i ($\rho_i$) e la densidade no estado f ($\rho_f$) como:
| $\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$ |
ID:(15687, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ p_i V_i = C_b $
p * V = C_b
$ p_f V_f = C_b $
p * V = C_b
$ p_i V_i = p_f V_f $
p_i * V_i = p_f * V_f
$\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$
p_i / rho_i = p_f / rho_f
$ \rho_i \equiv\displaystyle\frac{ M }{ V_i }$
rho = M / V
$ \rho_f \equiv\displaystyle\frac{ M }{ V_f }$
rho = M / V
ID:(15313, 0)
Lei de Boyle (1)
Equação
A lei de Boyle estabelece uma relação entre o volume ($V$) e la pressão ($p$), afirmando que seu produto é igual a la constante da lei de Boyle ($C_b$), da seguinte maneira:
| $ p_i V_i = C_b $ |
| $ p V = C_b $ |
ID:(582, 1)
Lei de Boyle (2)
Equação
A lei de Boyle estabelece uma relação entre o volume ($V$) e la pressão ($p$), afirmando que seu produto é igual a la constante da lei de Boyle ($C_b$), da seguinte maneira:
| $ p_f V_f = C_b $ |
| $ p V = C_b $ |
ID:(582, 2)
Mudança de estado de um gás ideal de acordo com a lei de Boyle
Equação
Se um gás passa de um estado inicial (i) para um estado final (f) com la temperatura absoluta ($T$) constante, a seguinte relação é válida para la pressão no estado inicial ($p_i$), la pressão em estado final ($p_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$):
| $ p_i V_i = p_f V_f $ |
A lei de Boyle estabelece que, com la temperatura absoluta ($T$) constante, o produto de la pressão ($p$) e o volume ($V$) é igual a la constante da lei de Boyle ($C_b$):
| $ p V = C_b $ |
Isso significa que, se um gás passar de um estado inicial (la pressão no estado inicial ($p_i$) e o volume no estado i ($V_i$)) para um estado final (la pressão em estado final ($p_f$) e o volume no estado f ($V_f$)), mantendo la temperatura absoluta ($T$) constante, ele deve sempre cumprir a lei de Boyle:
$p_i V_i = C_b = p_f V_f$
Portanto, tem-se que:
| $ p_i V_i = p_f V_f $ |
ID:(3491, 0)
Massa e Densidade (1)
Equação
La densidade ($\rho$) é definido como a relação entre la massa ($M$) e o volume ($V$), expressa como:
| $ \rho_i \equiv\displaystyle\frac{ M }{ V_i }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Essa propriedade é específica do material em questão.
ID:(3704, 1)
Massa e Densidade (2)
Equação
La densidade ($\rho$) é definido como a relação entre la massa ($M$) e o volume ($V$), expressa como:
| $ \rho_f \equiv\displaystyle\frac{ M }{ V_f }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Essa propriedade é específica do material em questão.
ID:(3704, 2)
Equivalente à lei de Boyle para densidades
Equação
A lei de Boyle para o estado inicial (la densidade no estado i ($\rho_i$), la pressão no estado inicial ($p_i$)) e o estado final (la densidade no estado f ($\rho_f$), la pressão em estado final ($p_f$)) é dada por:
| $\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$ |
Se, em uma mudança isotérmica em que o conteúdo não varia, la pressão no estado inicial ($p_i$), la pressão em estado final ($p_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$) estão relacionados por:
| $ p_i V_i = p_f V_f $ |
Então, podemos introduzir la densidade ($\rho$), que, junto com la massa ($M$) e o volume ($V$), satisfaz:
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
O que nos leva a la densidade no estado i ($\rho_i$) e la densidade no estado f ($\rho_f$) como:
| $\displaystyle\frac{ p_i }{ \rho_i } = \displaystyle\frac{ p_f }{ \rho_f }$ |
ID:(8834, 0)