Linsenfokus
Storyboard 
Der Fokus einer Linse kann aus den Krümmungsradien beider Seiten der Linse berechnet werden.
Bei einer Linse endlicher Dicke hängt der Fokus auch vom Brechungsindex des Mediums (Glas) und der Dicke auf der optischen Achse ab.
ID:(1442, 0)
Linsenfokus
Beschreibung 
Der Fokus einer Linse kann aus den Krümmungsradien beider Seiten der Linse berechnet werden.\\n\\nBei einer Linse endlicher Dicke hängt der Fokus auch vom Brechungsindex des Mediums (Glas) und der Dicke auf der optischen Achse ab.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
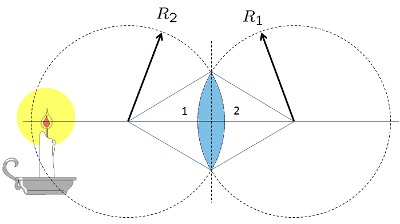
Lente Bi-Convexo grueso
(ID 1857)
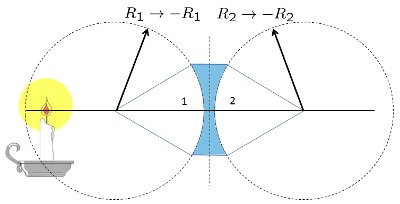
Lente Bi-Concavo grueso
(ID 12755)
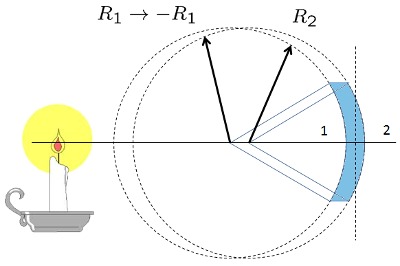
Lente c ncavo-convexo grueso
(ID 12757)
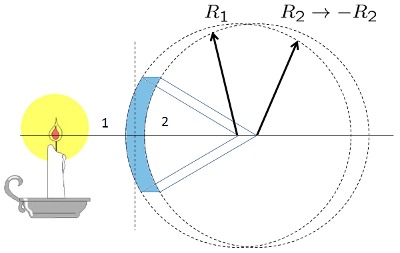
Lente convexo-concavo grueso
(ID 12756)
ID:(1442, 0)
