Utilisateur:
Accélération angulaire instantanée
Storyboard 
Pour décrire comment la vitesse angulaire évolue au fil du temps, il est nécessaire d'étudier sa variation dans le temps.
La relation de la variation de la vitesse angulaire équivaut à la variation de la vitesse angulaire sur le temps écoulé, qui, lorsqu'elle est divisée par ce temps, correspond à l'accélération angulaire.
Pour un intervalle de temps infinitésimal, l'accélération angulaire correspond à l'accélération angulaire instantanée.
ID:(1452, 0)
Accélération angulaire instantanée
Storyboard
Pour décrire comment la vitesse angulaire évolue au fil du temps, il est nécessaire d'étudier sa variation dans le temps. La relation de la variation de la vitesse angulaire équivaut à la variation de la vitesse angulaire sur le temps écoulé, qui, lorsqu'elle est divisée par ce temps, correspond à l'accélération angulaire. Pour un intervalle de temps infinitésimal, l'accélération angulaire correspond à l'accélération angulaire instantanée.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
tant donn que l'acc l ration tangentielle est
Si le vecteur unitaire de l'axe est $\hat{n}$ et le vecteur unitaire radial est $\hat{r}$, le vecteur unitaire tangentiel peut tre calcul l'aide du produit vectoriel :
$\hat{t} = \hat{n} \times \hat{r}$
En cons quence, en consid rant que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
et
$\vec{\alpha} = \alpha \hat{n}$
,
nous pouvons d duire que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
ce qui se traduit par
Exemples
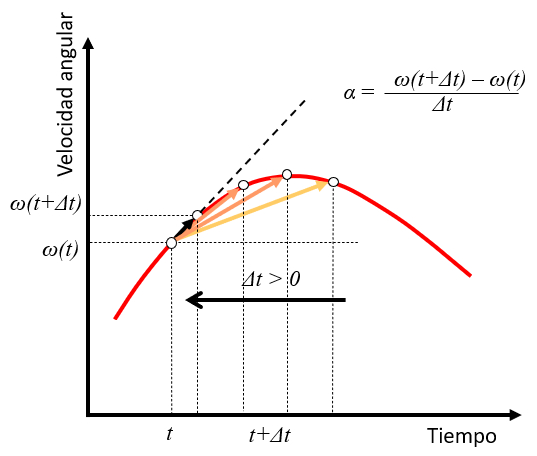
Si l'on consid re un intervalle de temps $t$ avec une vitesse angulaire $\omega(t)$ et qu'un point est observ un moment futur $t+\Delta t$ avec une vitesse angulaire $\omega(t+\Delta t)$, l'acc l ration angulaire peut tre estim e comme la variation
$\omega(t+\Delta t)-\omega(t)$
au cours du temps $\Delta t$ :
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
mesure que la valeur de $\Delta t$ diminue, l'acc l ration prend le r le de la tangente la courbe de vitesse ce moment-l :
Ceci g n ralise ce qui a d j t observ dans le cas de l'acc l ration angulaire constante.
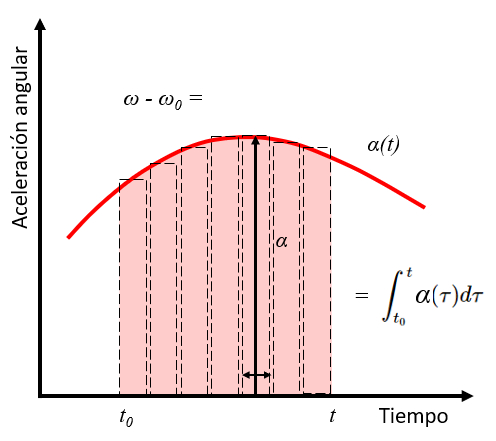
La int grale d'une fonction correspond l'aire sous la courbe qui d finit cette fonction. Ainsi, l\'int grale de l\'acc l ration angulaire entre les instants $t_0$ et $t$ correspond la variation de la vitesse angulaire entre la vitesse angulaire initiale $\omega_0$ et $\omega$.
Par cons quent, en utilisant
Ce qui est repr sent sur le graphique suivant :
L'orientation de l'acc l ration tangentielle peut tre obtenue en utilisant la r gle de la main droite, o les doigts pointent vers l'axe, puis tournent vers le rayon :
Tout comme dans le cas de l'acc l ration de translation, il existe le concept d'acc l ration angulaire instantan e, qui est l'acc l ration angulaire avec
qui existe un moment sp cifique. Cela est calcul dans l'approximation de tr s petits intervalles de temps $(\Delta t\rightarrow 0)$, c'est- -dire
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
o
Si nous int grons la d finition de la vitesse angulaire par rapport au temps, en utilisant
Cela signifie que, pour un intervalle de temps $dt$, l'angle parcouru est donn par :
$d\omega = \alpha dt$
Si nous consid rons $N$ intervalles $dt_i$ avec les vitesses angulaires correspondantes $\alpha_i$, l'angle total parcouru sera :
$\omega - \omega_0 = \sum_i \alpha_i dt_i$
En consid rant la courbe de vitesse angulaire-temps, les l ments $\alpha_i dt_i$ correspondent des rectangles avec une hauteur $\alpha_i$ et une largeur $dt_i$. La somme correspond donc l'aire sous la courbe de vitesse angulaire-temps. Ainsi, la somme peut tre exprim e comme une int grale en utilisant
En g n ral, il faut comprendre l'acc l ration comme une grandeur tridimensionnelle, c'est- -dire vectorielle. Cela signifie que sa vitesse doit tre d crite par un vecteur vitesse angulaire $\vec{\omega}$ pour lequel on peut d finir une composante d'acc l ration avec
Ainsi, on peut g n raliser l\'acc l ration avec :
L'int gration de la d finition diff rentielle, c'est- -dire des variations temporelles infinit simales, par rapport l\' quation
Nous pouvons effectuer l\'int gration entre le temps $t_0$ et $t$ de l\'acc l ration $a(\tau)$ pour obtenir la vitesse $v(t)$ si la vitesse initiale est $v_0$, en utilisant l\' quation:
L'acc l ration angulaire est repr sent e sous forme de vecteur dans la direction de l'axe de rotation. tant donn que le rayon de rotation et l'acc l ration angulaire sont orthogonaux l'acc l ration tangentielle, nous avons :
Cette relation peut tre exprim e sous forme de produit vectoriel entre l'acc l ration angulaire et le rayon, crit comme suit :
ID:(1452, 0)
