Instantaneous angular acceleration
Storyboard 
To describe how angular velocity evolves over time, one must examine its variation with respect to time.
The relationship of the change in angular velocity corresponds to the angular displacement covered over the elapsed time, which when divided by this time, yields the angular acceleration.
For an infinitesimally small time interval, the angular acceleration corresponds to the instantaneous angular acceleration.
ID:(1452, 0)
Angular acceleration as a derivative
Image 
If a time $t$ is taken with an angular velocity $\omega(t)$ and a point is observed at a future time $t+\Delta t$ with an angular velocity $\omega(t+\Delta t)$, the angular acceleration can be estimated as the variation
$\omega(t+\Delta t)-\omega(t)$
over time $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
As the value of $\Delta t$ decreases, the acceleration takes on the role of the tangent to the velocity curve at that time:
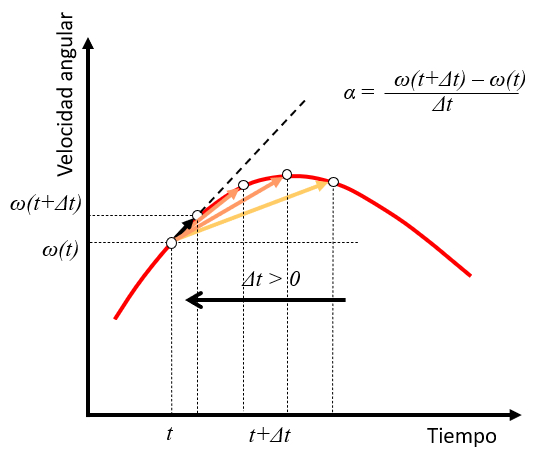
This generalizes what has already been seen for the case of constant angular acceleration.
ID:(11413, 0)
Angular Velocity as Integral of Acceleration
Note 
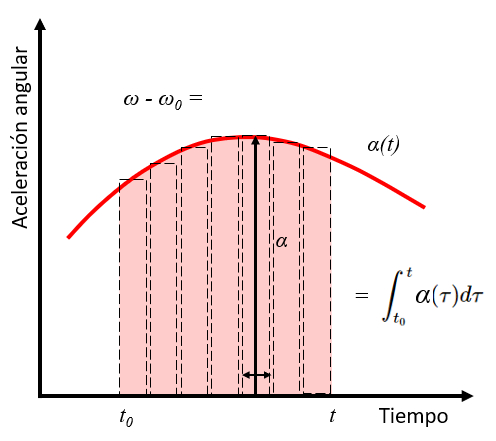
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of angular acceleration between the times $t_0$ and $t$ corresponds to the change in angular velocity between the initial angular velocity $\omega_0$ and $\omega$.
Thus, using , we obtain:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
This is illustrated in the following graph:
ID:(11415, 0)
Tangential acceleration, right hand rule
Quote 
The orientation of tangential acceleration can be obtained using the right-hand rule, with fingers pointing towards the axis and then rotating towards the radius:

ID:(11600, 0)
Instantaneous angular acceleration
Storyboard 
To describe how angular velocity evolves over time, one must examine its variation with respect to time. The relationship of the change in angular velocity corresponds to the angular displacement covered over the elapsed time, which when divided by this time, yields the angular acceleration. For an infinitesimally small time interval, the angular acceleration corresponds to the instantaneous angular acceleration.
Variables
Calculations
Calculations
Equations
Given that the tangential acceleration is
If the unit vector of the axis is $\hat{n}$ and the radial unit vector is $\hat{r}$, the tangential unit vector can be calculated using the cross product:
$\hat{t} = \hat{n} \times \hat{r}$
As a result, considering that
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
, and
$\vec{\alpha} = \alpha \hat{n}$
,
we can deduce that
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
which translates to
Examples
If a time $t$ is taken with an angular velocity $\omega(t)$ and a point is observed at a future time $t+\Delta t$ with an angular velocity $\omega(t+\Delta t)$, the angular acceleration can be estimated as the variation
$\omega(t+\Delta t)-\omega(t)$
over time $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
As the value of $\Delta t$ decreases, the acceleration takes on the role of the tangent to the velocity curve at that time:
This generalizes what has already been seen for the case of constant angular acceleration.
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of angular acceleration between the times $t_0$ and $t$ corresponds to the change in angular velocity between the initial angular velocity $\omega_0$ and $\omega$.
Thus, using
This is illustrated in the following graph:
The orientation of tangential acceleration can be obtained using the right-hand rule, with fingers pointing towards the axis and then rotating towards the radius:
Similar to translational acceleration, there is the concept of Instantaneous Angular Acceleration, which is the angular acceleration with
that exists at a specific time. This is calculated in the approximation of very small time intervals $(\Delta t\rightarrow 0)$, meaning
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
where
If we integrate the definition of angular velocity with respect to time, using
This means that for a time interval $dt$, the traversed angle is given by:
$d\omega = \alpha dt$
If we consider $N$ intervals $dt_i$ with corresponding angular velocities $\alpha_i$, the total traversed angle will be:
$\omega - \omega_0 = \sum_i \alpha_i dt_i$
Considering the angular velocity-time curve, the elements $\alpha_i dt_i$ correspond to rectangles with height $\alpha_i$ and width $dt_i$. The sum, therefore, corresponds to the area under the angular velocity-time curve. Hence, the sum can be expressed as an integral using
En general, la aceleraci n debe entenderse como una entidad tridimensional, es decir, vectorial. Esto significa que su velocidad debe ser descrita por un vector de velocidad angular $\vec{\omega}$, para el cual se puede definir una componente de aceleraci n con
De este modo, se puede generalizar la aceleraci n como:
The integration of the differential definition, i.e., infinitesimal temporal variations, with respect to equation
We can perform integration between time $t_0$ and $t$ of the acceleration $a(\tau)$ to obtain the velocity $v(t)$ if the initial velocity is $v_0$, using the equation:
Angular acceleration is represented as a vector aligned with the axis of rotation. Because the radius of rotation and angular acceleration are orthogonal to tangential acceleration, we have:
This relationship can be expressed as the cross product of angular acceleration and radius, written as:
ID:(1452, 0)
