Benützer:
Nutzung von Kapazitäten
Storyboard 
Kapazität sind Kurzstrecken-Metallplatten, die durch Anschließen an eine Potentialdifferenz aufgeladen werden können. Auf diese Weise entsteht eine Platte mit negativen Ladungen (Elektronen) und der anderen positiven (Mangel an Elektronen, so dass die positiven Ladungen der Leiterstruktur überwiegen), die durch die Anziehung zwischen Ladungen unterschiedlicher Vorzeichen an Ort und Stelle gehalten werden. Sobald beide Pole durch einen Leiter verbunden sind, fließt Strom, bis er vollständig entladen ist, wobei die Last auf beiden Platten ausgeglichen wird.
ID:(816, 0)
Nutzung von Kapazitäten
Beschreibung
Kapazität sind Kurzstrecken-Metallplatten, die durch Anschließen an eine Potentialdifferenz aufgeladen werden können. Auf diese Weise entsteht eine Platte mit negativen Ladungen (Elektronen) und der anderen positiven (Mangel an Elektronen, so dass die positiven Ladungen der Leiterstruktur überwiegen), die durch die Anziehung zwischen Ladungen unterschiedlicher Vorzeichen an Ort und Stelle gehalten werden. Sobald beide Pole durch einen Leiter verbunden sind, fließt Strom, bis er vollständig entladen ist, wobei die Last auf beiden Platten ausgeglichen wird.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
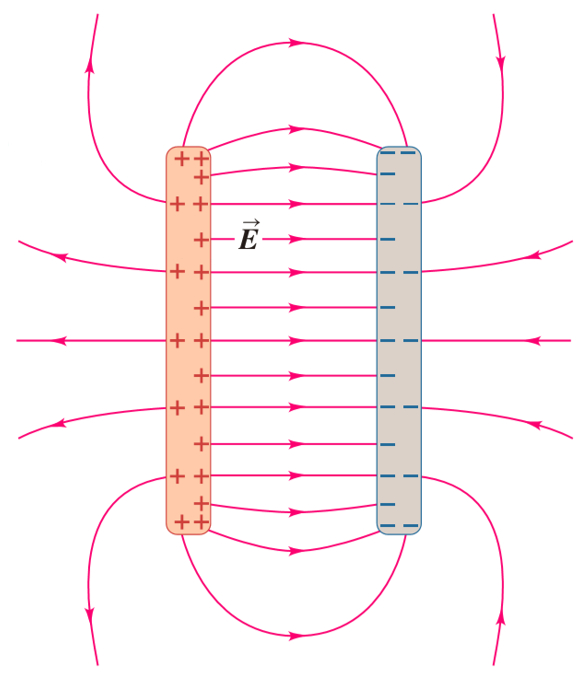
Bei zwei Platten mit entgegengesetzten Ladungen besteht zwischen ihnen ein Feld gr erer Intensit t. Es gibt jedoch ein kleines Feld, das mit Feldlinien beschrieben werden kann, die aus einer der Platten austreten und durch eine u ere Drehung der gegen berliegenden Platte zur ckkehren:
(ID 11454)
ID:(816, 0)