Usuario:
Método del plano
Storyboard 
Las laderas presentan el problema de que el suelo puede deslizarse si las fuerzas generadas por su propio peso superan la cohesión del suelo. Dado que la cohesión puede variar debido a factores externos, existe la posibilidad de que una masa pierda estabilidad y se desplace, por lo que es crucial comprender su vulnerabilidad y la probabilidad de que pueda desestabilizarse en el futuro.
ID:(383, 0)
Geometría del suelo a deslizarse
Descripción
Para modelar la estabilidad de un terreno asumimos un fondo rocoso con una pendiente dada y una capa de suelo homogénea que se puede deslizar sobre esta.
ID:(1134, 0)
Fuerzas gravitacionales y roce
Imagen
En primera instancia podemos considerar que la masa genera una fuerza gravitacional que trata de deslizar el suelo por la pendiente. Por otro lado la componente vertical al fondo rocoso genera el roce necesario para mantener la masa en su lugar:
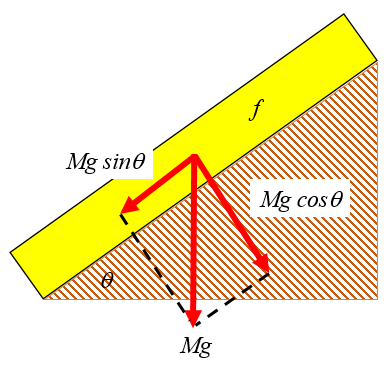
Modelo de quiebre
De no existir agua ambas fuerzas son proporcionales a la masa por lo que finalmente solo dependerá del coeficiente de roce si la capa es estable.
ID:(2970, 0)
Rol del agua en el suelo
Imagen
De existir agua en el suelo esta contribuye en varias formas para desestabilizar la capa de suelo. Una primera forma es creando una fuerza de sustentación que reduce la fuerza normal y con ello el roce que sujeta el suelo en el lugar:
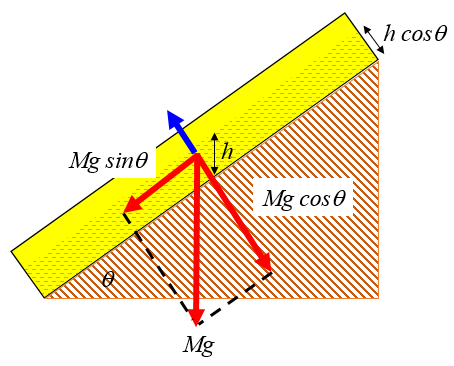
Caso corto
Este comportamiento corresponde a lo que se podría llamar en el limite la tendencia a que el suelo flote.
ID:(7985, 0)
Fuerzas de adhesión entre granos
Imagen
La segunda contribución del agua tiende, en la medida que el agua este adecuadamente dosificada, a estabilizar el suelo. Si solo figura como humedad relativa alta se forman meniscos de agua entre los granos que ejercen fuerzas cohesivas. Sin embargo si la capa de suelo es inundada dicha sección pierde esta cohesión y es el resto sobre el nivel del agua que debe soportar el peso de la masa:
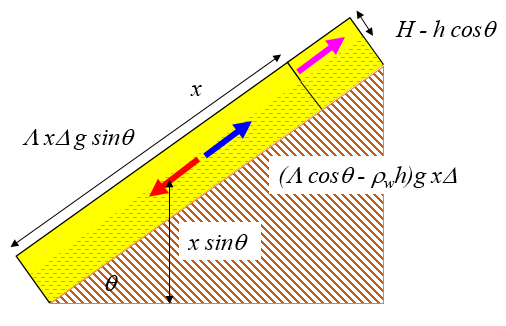
ID:(7986, 0)
Modelo de cohesión y ángulo de fricción Interna
Concepto
Tanto la cohesión del material ($c$) como el ángulo de fricción interna del suelo ($\phi$) dependen de la composición del suelo (la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$), la fracción de masa de arcilla en la muestra ($g_c$)) y del contenido de agua (la fracción de masa del agua en la muestra ($g_w$)).
A partir de mediciones, se pueden desarrollar modelos fenomenológicos que describen estas propiedades:
Modelo de Cohesión
La cohesión la cohesión del material ($c$) se expresa mediante la ecuación:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
Donde las constantes la cohesión inherente del material seco ($c_0$), la grado de cohesión inducido por partículas finas ($k$), y la sensibilidad de la cohesión al agua ($m$) toman los siguientes valores típicos:
• la cohesión inherente del material seco ($c_0$):
| Suelos arenosos | 0-5 kPa |
| Suelos limosos | 5-15 kPa |
| Suelos arcillosos | 15-50 kPa |
• la grado de cohesión inducido por partículas finas ($k$): 20 - 200 kPa
• la sensibilidad de la cohesión al agua ($m$): 5 - 20 kPa
Modelo del Ángulo de Fricción Interna
El ángulo de fricción interna el ángulo de fricción interna del suelo ($\phi$) se describe mediante la ecuación:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
Donde las constantes el ángulo de fricción interna del suelo base ($\phi_0$), la sensibilidad del angulo de fricción a la arcilla ($k_c$), la sensibilidad del angulo de fricción a la arena ($k_a$), y la sensibilidad del angulo de fricción al agua ($k_w$) toman los valores:
• el ángulo de fricción interna del suelo base ($\phi_0$):
| Arena seca | 30° - 40° |
| Limos secos | 20° - 30° |
| Arcillas compactas | 15° - 25° |
• la sensibilidad del angulo de fricción a la arcilla ($k_c$): 5° - 10°
• la sensibilidad del angulo de fricción a la arena ($k_a$): 3° - 8°
• la sensibilidad del angulo de fricción al agua ($k_w$): 5° - 15°
ID:(16125, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ c = c_0 + k ( g_i + g_c ) - m g_w$
c = c_0 + k *( g_i + g_c ) - m * g_w
$ \gamma_s = \rho_s g $
gamma_s = rho_s * g
$ \gamma_w = \rho_w g $
gamma_w = rho_w * g
$ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$
phi = phi_0 + k_a * g_a - k_c * g_c - k_w * g_w
$ p_v = s \gamma_w H $
p_v = s * gamma_w * H
$ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $
SF = ( c + ( sigma - p_v )*tan( phi ))/ tau
$ \sigma = \gamma_s H \cos \theta $
sigma = gamma_s * H *cos( theta )
$ \tau = \gamma_s H \sin \theta $
tau = gamma_s * H *sin( theta )
ID:(16105, 0)
Factor de seguridad
Ecuación
El el factor de seguridad ($SF$) representa la proporción de la tensión que evita el deslizamiento. Se calcula a partir de la cohesión del material ($c$), ajustado por la tensión normal ($\sigma$), con una reducción de la presión del agua en los poros ($p_v$) y ponderado mediante la tangente de el ángulo de fricción interna del suelo ($\phi$) y la tensión normal ($\sigma$), utilizando la siguiente expresión:
| $ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $ |
ID:(16112, 0)
Esfuerzo cortante
Ecuación
El esfuerzo cortante ($\tau$) se calcula a partir de peso unitario del suelo ($\gamma_s$), combinado con la altura de la capa ($H$) y ponderado por el seno de el ángulo de pendiente de la ladera ($\theta$), según la siguiente fórmula:
| $ \tau = \gamma_s H \sin \theta $ |
ID:(16111, 0)
Peso unitario del agua
Ecuación
peso unitario del agua ($\gamma_w$) del agua se determina a partir de la densidad del agua ($\rho_w$) y la aceleración gravitacional ($g$), aplicando la fórmula siguiente:
| $ \gamma_w = \rho_w g $ |
ID:(16108, 0)
Peso unitario del suelo
Ecuación
peso unitario del suelo ($\gamma_s$) de un cuerpo se calcula utilizando la densidad sólida ($\rho_s$) y la aceleración gravitacional ($g$), según la siguiente fórmula:
| $ \gamma_s = \rho_s g $ |
ID:(16107, 0)
Presión del agua en los poros
Ecuación
La presión del agua en los poros ($p_v$) generada por el agua en los poros se calcula a partir de el saturación ($s$), peso unitario del agua ($\gamma_w$) y la altura de la capa ($H$), utilizando la siguiente fórmula:
| $ p_v = s \gamma_w H $ |
ID:(16110, 0)
Tensión normal
Ecuación
La tensión normal ($\sigma$) es la tensión que contrarresta el deslizamiento, y se calcula a partir de peso unitario del suelo ($\gamma_s$), la altura de la capa ($H$) y el ángulo de pendiente de la ladera ($\theta$), utilizando la fórmula siguiente:
| $ \sigma = \gamma_s H \cos \theta $ |
ID:(16109, 0)
Modelo de cohesión
Ecuación
La cohesión del material ($c$) puede estimarse a partir de la cohesión inherente del material seco ($c_0$), la grado de cohesión inducido por partículas finas ($k$), la sensibilidad de la cohesión al agua ($m$), la fracción de masa de arcilla en la muestra ($g_c$), la fracción de masa de limo en la muestra ($g_i$), y la fracción de masa del agua en la muestra ($g_w$), utilizando la siguiente fórmula:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
ID:(16123, 0)
Modelo del ángulo de fricción interna
Ecuación
El ángulo de fricción interna del suelo ($\phi$) puede estimarse a partir de el ángulo de fricción interna del suelo base ($\phi_0$), la sensibilidad del angulo de fricción a la arcilla ($k_c$), la sensibilidad del angulo de fricción a la arena ($k_a$), la sensibilidad del angulo de fricción al agua ($k_w$), la fracción de masa de arcilla en la muestra ($g_c$), la fracción de masa de arena en la muestra ($g_a$), y la fracción de masa del agua en la muestra ($g_w$), utilizando la siguiente fórmula:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
ID:(16124, 0)