Benützer:
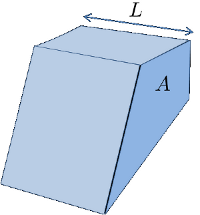
Flächenmethode
Storyboard 
Hänge haben das Problem, dass der Boden rutschen kann, wenn die durch das Eigengewicht erzeugten Kräfte die Kohäsion des Bodens überschreiten. Da die Kohäsion aufgrund externer Faktoren variieren kann, besteht die Möglichkeit, dass eine Masse an Stabilität verliert und sich verschiebt. Daher ist es entscheidend, die Verwundbarkeit und die Wahrscheinlichkeit zukünftiger Destabilisierung zu verstehen.
ID:(383, 0)
Geometrie der Böschung
Beschreibung
Para modelar la estabilidad de un terreno asumimos un fondo rocoso con una pendiente dada y una capa de suelo homogénea que se puede deslizar sobre esta.
ID:(1134, 0)
Fuerzas gravitacionales y roce
Bild
En primera instancia podemos considerar que la masa genera una fuerza gravitacional que trata de deslizar el suelo por la pendiente. Por otro lado la componente vertical al fondo rocoso genera el roce necesario para mantener la masa en su lugar:
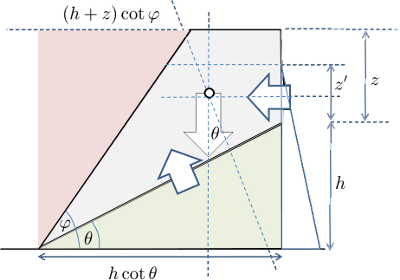
De no existir agua ambas fuerzas son proporcionales a la masa por lo que finalmente solo dependerá del coeficiente de roce si la capa es estable.
ID:(2970, 0)
Rol del agua en el suelo
Bild
De existir agua en el suelo esta contribuye en varias formas para desestabilizar la capa de suelo. Una primera forma es creando una fuerza de sustentación que reduce la fuerza normal y con ello el roce que sujeta el suelo en el lugar:
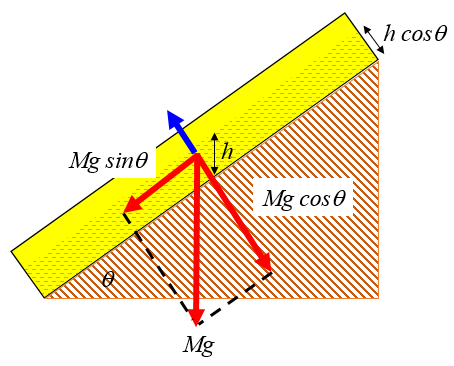
Este comportamiento corresponde a lo que se podría llamar en el limite la tendencia a que el suelo flote.
ID:(7985, 0)
Fuerzas de adhesión entre granos
Bild
La segunda contribución del agua tiende, en la medida que el agua este adecuadamente dosificada, a estabilizar el suelo. Si solo figura como humedad relativa alta se forman meniscos de agua entre los granos que ejercen fuerzas cohesivas. Sin embargo si la capa de suelo es inundada dicha sección pierde esta cohesión y es el resto sobre el nivel del agua que debe soportar el peso de la masa:
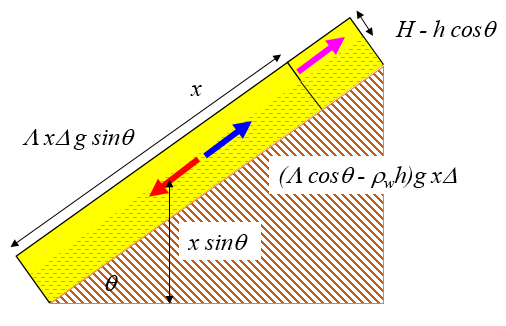
ID:(7986, 0)
Modell der Kohäsion und des inneren Reibungswinkels
Konzept
Sowohl die Materialkohäsion ($c$) als auch der Bodeninterner Reibungswinkel ($\phi$) hängen von der Zusammensetzung des Bodens (die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$), die Massenanteil von Ton in der Probe ($g_c$)) und dem Wassergehalt (die Massenanteil an Wasser in der Probe ($g_w$)) ab.
Basierend auf Messungen können phänomenologische Modelle entwickelt werden, die diese Eigenschaften beschreiben:
Kohäsionsmodell
Die Kohäsion die Materialkohäsion ($c$) wird durch die folgende Gleichung beschrieben:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
Dabei nehmen die Konstanten die Inhärenter Zusammenhalt des trockenen Materials ($c_0$), die Grad der durch feine Partikel hervorgerufenen Kohäsion ($k$) und die Kohäsionsempfindlichkeit gegenüber Wasser ($m$) die folgenden typischen Werte an:
• die Inhärenter Zusammenhalt des trockenen Materials ($c_0$):
| Sandige Böden | 0-5 kPa |
| Schluffige Böden | 5-15 kPa |
| Tonige Böden | 15-50 kPa |
• die Grad der durch feine Partikel hervorgerufenen Kohäsion ($k$): 20 - 200 kPa
• die Kohäsionsempfindlichkeit gegenüber Wasser ($m$): 5 - 20 kPa
Modell des inneren Reibungswinkels
Der innere Reibungswinkel der Bodeninterner Reibungswinkel ($\phi$) wird durch die folgende Gleichung beschrieben:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
Dabei nehmen die Konstanten der Interner Reibungswinkel des Grundbodens ($\phi_0$), die Reibungswinkelempfindlichkeit gegenüber Ton ($k_c$), die Reibungswinkelempfindlichkeit gegenüber Sand ($k_a$) und die Reibungswinkelempfindlichkeit gegenüber Wasser ($k_w$) die folgenden Werte an:
• der Interner Reibungswinkel des Grundbodens ($\phi_0$):
| Trockener Sand | 30° - 40° |
| Trockener Schluff | 20° - 30° |
| Kompakter Ton | 15° - 25° |
• die Reibungswinkelempfindlichkeit gegenüber Ton ($k_c$): 5° - 10°
• die Reibungswinkelempfindlichkeit gegenüber Sand ($k_a$): 3° - 8°
• die Reibungswinkelempfindlichkeit gegenüber Wasser ($k_w$): 5° - 15°
ID:(16125, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ c = c_0 + k ( g_i + g_c ) - m g_w$
c = c_0 + k *( g_i + g_c ) - m * g_w
$ \gamma_s = \rho_s g $
gamma_s = rho_s * g
$ \gamma_w = \rho_w g $
gamma_w = rho_w * g
$ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$
phi = phi_0 + k_a * g_a - k_c * g_c - k_w * g_w
$ p_v = s \gamma_w H $
p_v = s * gamma_w * H
$ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $
SF = ( c + ( sigma - p_v )*tan( phi ))/ tau
$ \sigma = \gamma_s H \cos \theta $
sigma = gamma_s * H *cos( theta )
$ \tau = \gamma_s H \sin \theta $
tau = gamma_s * H *sin( theta )
ID:(16105, 0)
Sicherheitsfaktor
Gleichung
Der der Sicherheitsfaktor ($SF$) stellt das Verhältnis der Spannung dar, die ein Gleiten verhindert. Er wird auf Basis von die Materialkohäsion ($c$) berechnet, angepasst durch die Normale Spannung ($\sigma$), reduziert um die Wasserdruck in den Poren ($p_v$) und gewichtet mit der Tangente von der Bodeninterner Reibungswinkel ($\phi$) und die Normale Spannung ($\sigma$), wie in der folgenden Gleichung dargestellt:
| $ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $ |
ID:(16112, 0)
Schubspannung
Gleichung
Der Scherbeanspruchung ($\tau$) wird aus Einheitsgewicht des Bodens ($\gamma_s$) berechnet, kombiniert mit die Schichthöhe ($H$) und gewichtet mit dem Sinus von der Neigungswinkel der Hangfläche ($\theta$), wie in der folgenden Formel dargestellt:
| $ \tau = \gamma_s H \sin \theta $ |
ID:(16111, 0)
Spezifisches Gewicht des Wassers
Gleichung
Einheitsgewicht von Wasser ($\gamma_w$) des Wassers wird aus die Wasserdichte ($\rho_w$) und die Gravitationsbeschleunigung ($g$) mithilfe der folgenden Formel berechnet:
| $ \gamma_w = \rho_w g $ |
ID:(16108, 0)
Spezifisches Gewicht des Bodens
Gleichung
Einheitsgewicht des Bodens ($\gamma_s$) eines Körpers wird mithilfe von die Festkörperdichte ($\rho_s$) und die Gravitationsbeschleunigung ($g$) berechnet, wie in der folgenden Formel dargestellt:
| $ \gamma_s = \rho_s g $ |
ID:(16107, 0)
Porenwasserdruck
Gleichung
Die Wasserdruck in den Poren ($p_v$), der durch Wasser in den Poren erzeugt wird, wird aus der Sättigung ($s$), Einheitsgewicht von Wasser ($\gamma_w$) und die Schichthöhe ($H$) berechnet, wie in der folgenden Formel dargestellt:
| $ p_v = s \gamma_w H $ |
ID:(16110, 0)
Normale Spannung
Gleichung
Die Normale Spannung ($\sigma$) ist die Spannung, die das Gleiten entgegenwirkt, und wird mithilfe von Einheitsgewicht des Bodens ($\gamma_s$), die Schichthöhe ($H$) und der Neigungswinkel der Hangfläche ($\theta$) berechnet, wie in der folgenden Formel dargestellt:
| $ \sigma = \gamma_s H \cos \theta $ |
ID:(16109, 0)
Kohäsionsmodell
Gleichung
Die Materialkohäsion ($c$) kann mit die Inhärenter Zusammenhalt des trockenen Materials ($c_0$), die Grad der durch feine Partikel hervorgerufenen Kohäsion ($k$), die Kohäsionsempfindlichkeit gegenüber Wasser ($m$), die Massenanteil von Ton in der Probe ($g_c$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil an Wasser in der Probe ($g_w$) anhand der folgenden Formel geschätzt werden:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
ID:(16123, 0)
Modell des inneren Reibungswinkels
Gleichung
Der Bodeninterner Reibungswinkel ($\phi$) kann anhand von der Interner Reibungswinkel des Grundbodens ($\phi_0$), die Reibungswinkelempfindlichkeit gegenüber Ton ($k_c$), die Reibungswinkelempfindlichkeit gegenüber Sand ($k_a$), die Reibungswinkelempfindlichkeit gegenüber Wasser ($k_w$), die Massenanteil von Ton in der Probe ($g_c$), die Massenanteil von Sand in der Probe ($g_a$) und die Massenanteil an Wasser in der Probe ($g_w$) mit der folgenden Formel geschätzt werden:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
ID:(16124, 0)