User:
Plane method
Storyboard 
Slopes have the issue that the soil can slide if the forces generated by its own weight exceed the soil's cohesion. Since cohesion can vary due to external factors, there is a possibility that a mass may lose stability and shift, making it essential to understand its vulnerability and the likelihood of future destabilization.
ID:(383, 0)
Geometry of the Embankment
Description
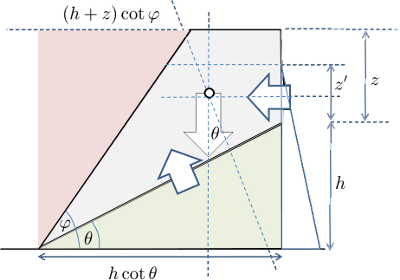
Para modelar la estabilidad de un terreno asumimos un fondo rocoso con una pendiente dada y una capa de suelo homogénea que se puede deslizar sobre esta.
ID:(1134, 0)
Fuerzas gravitacionales y roce
Image
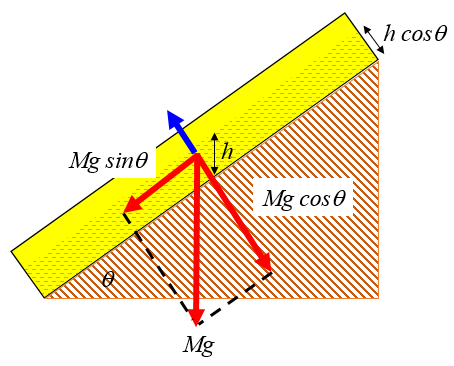
En primera instancia podemos considerar que la masa genera una fuerza gravitacional que trata de deslizar el suelo por la pendiente. Por otro lado la componente vertical al fondo rocoso genera el roce necesario para mantener la masa en su lugar:
De no existir agua ambas fuerzas son proporcionales a la masa por lo que finalmente solo dependerá del coeficiente de roce si la capa es estable.
ID:(2970, 0)
Rol del agua en el suelo
Image
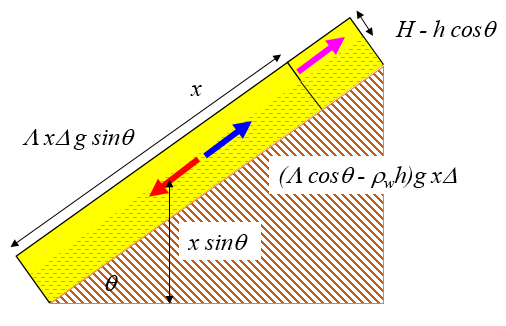
De existir agua en el suelo esta contribuye en varias formas para desestabilizar la capa de suelo. Una primera forma es creando una fuerza de sustentación que reduce la fuerza normal y con ello el roce que sujeta el suelo en el lugar:
Este comportamiento corresponde a lo que se podrÃa llamar en el limite la tendencia a que el suelo flote.
ID:(7985, 0)
Fuerzas de adhesión entre granos
Image
La segunda contribución del agua tiende, en la medida que el agua este adecuadamente dosificada, a estabilizar el suelo. Si solo figura como humedad relativa alta se forman meniscos de agua entre los granos que ejercen fuerzas cohesivas. Sin embargo si la capa de suelo es inundada dicha sección pierde esta cohesión y es el resto sobre el nivel del agua que debe soportar el peso de la masa:
ID:(7986, 0)
Cohesion and Internal friction angle model
Concept
The cohesion of the material ($c$) and the angle of internal friction of the soil ($\phi$) depend on the soil composition (the mass fraction of sand in the sample ($g_a$), the mass fraction of silt in the sample ($g_i$), the mass fraction of clay in the sample ($g_c$)) and water content (the mass fraction of water in the sample ($g_w$)).
Based on measurements, phenomenological models can be developed to describe these properties:
Cohesion Model
Cohesion the cohesion of the material ($c$) is expressed using the equation:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
Where the constants the inherent cohesion of dry material ($c_0$), the degree of cohesion induced by fine particles ($k$), and the sensitivity of cohesion to water ($m$) take the following typical values:
• the inherent cohesion of dry material ($c_0$):
| Sandy soils | 0-5 kPa |
| Loamy soils | 5-15 kPa |
| Clayey soils | 15-50 kPa |
• the degree of cohesion induced by fine particles ($k$): 20 - 200 kPa
• the sensitivity of cohesion to water ($m$): 5 - 20 kPa
Internal Friction Angle Model
The internal friction angle the angle of internal friction of the soil ($\phi$) is described using the equation:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
Where the constants the internal friction angle of the base soil ($\phi_0$), the friction angle sensitivity to clay ($k_c$), the friction angle sensitivity to sand ($k_a$), and the friction angle sensitivity to water ($k_w$) take the following values:
• the internal friction angle of the base soil ($\phi_0$):
| Dry sand | 30° - 40° |
| Dry loam | 20° - 30° |
| Compact clays | 15° - 25° |
• the friction angle sensitivity to clay ($k_c$): 5° - 10°
• the friction angle sensitivity to sand ($k_a$): 3° - 8°
• the friction angle sensitivity to water ($k_w$): 5° - 15°
ID:(16125, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ c = c_0 + k ( g_i + g_c ) - m g_w$
c = c_0 + k *( g_i + g_c ) - m * g_w
$ \gamma_s = \rho_s g $
gamma_s = rho_s * g
$ \gamma_w = \rho_w g $
gamma_w = rho_w * g
$ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$
phi = phi_0 + k_a * g_a - k_c * g_c - k_w * g_w
$ p_v = s \gamma_w H $
p_v = s * gamma_w * H
$ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $
SF = ( c + ( sigma - p_v )*tan( phi ))/ tau
$ \sigma = \gamma_s H \cos \theta $
sigma = gamma_s * H *cos( theta )
$ \tau = \gamma_s H \sin \theta $
tau = gamma_s * H *sin( theta )
ID:(16105, 0)
Factor of safety
Equation
The the security factor ($SF$) represents the ratio of the stress that prevents sliding. It is calculated based on the cohesion of the material ($c$), adjusted by the normal tension ($\sigma$), reduced by the water pressure in pores ($p_v$), and weighted using the tangent of the angle of internal friction of the soil ($\phi$) and the normal tension ($\sigma$), as expressed in the following equation:
| $ SF = \displaystyle\frac{ c + ( \sigma - p_v )\tan \phi }{ \tau } $ |
ID:(16112, 0)
Shear stress
Equation
The shear stress ($\tau$) is calculated from unit weight of soil ($\gamma_s$), combined with the layer height ($H$), and weighted by the sine of the slope angle of the hillside ($\theta$), as shown in the following formula:
| $ \tau = \gamma_s H \sin \theta $ |
ID:(16111, 0)
Unit weight of water
Equation
unit weight of water ($\gamma_w$) of water is determined from the water density ($\rho_w$) and the gravitational Acceleration ($g$), using the following formula:
| $ \gamma_w = \rho_w g $ |
ID:(16108, 0)
Unit weight of soil
Equation
unit weight of soil ($\gamma_s$) of a body is calculated using the solid Density ($\rho_s$) and the gravitational Acceleration ($g$), as expressed in the following formula:
| $ \gamma_s = \rho_s g $ |
ID:(16107, 0)
Pore water pressure
Equation
The water pressure in pores ($p_v$) generated by water in the pores is calculated using the saturation ($s$), unit weight of water ($\gamma_w$), and the layer height ($H$), as shown in the following formula:
| $ p_v = s \gamma_w H $ |
ID:(16110, 0)
Normal stress
Equation
The normal tension ($\sigma$) is the stress that counteracts sliding, calculated using unit weight of soil ($\gamma_s$), the layer height ($H$), and the slope angle of the hillside ($\theta$), as shown in the following formula:
| $ \sigma = \gamma_s H \cos \theta $ |
ID:(16109, 0)
Cohesion model
Equation
The cohesion of the material ($c$) can be estimated using the inherent cohesion of dry material ($c_0$), the degree of cohesion induced by fine particles ($k$), the sensitivity of cohesion to water ($m$), the mass fraction of clay in the sample ($g_c$), the mass fraction of silt in the sample ($g_i$), and the mass fraction of water in the sample ($g_w$), with the following formula:
| $ c = c_0 + k ( g_i + g_c ) - m g_w$ |
ID:(16123, 0)
Internal friction angle model
Equation
The angle of internal friction of the soil ($\phi$) can be estimated using the internal friction angle of the base soil ($\phi_0$), the friction angle sensitivity to clay ($k_c$), the friction angle sensitivity to sand ($k_a$), the friction angle sensitivity to water ($k_w$), the mass fraction of clay in the sample ($g_c$), the mass fraction of sand in the sample ($g_a$), and the mass fraction of water in the sample ($g_w$), with the following formula:
| $ \phi = \phi_0 + k_a g_a - k_c g_c - k_w g_w$ |
ID:(16124, 0)