Utilisateur:
Voie libre sur un gaz
Concept 
Quand une particule d'un gaz se déplace, elle interagit avec les autres particules. La forme la plus simple de cette interaction se produit à travers des collisions élastiques, ce qui signifie que la particule entre en collision sans perdre d'énergie, changeant sa direction pour ensuite entrer en collision avec une autre particule.
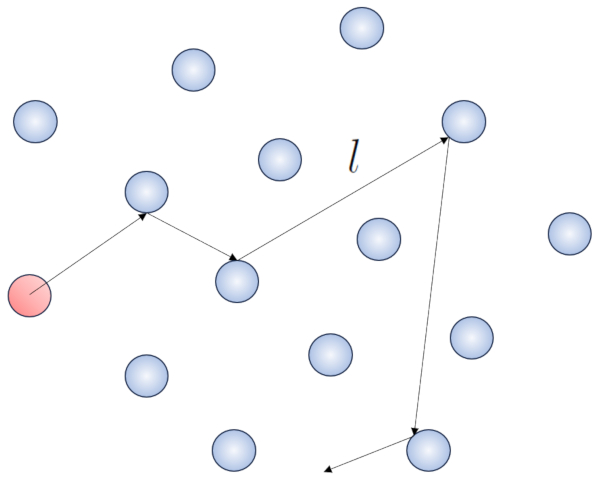
Dans ce processus, il est judicieux de définir le route libre ($\bar{l}$), dont la valeur dépendra de une concentration de particules ($c_n$).
ID:(1708, 0)
Cheminement libre sans circulation des voisins
Concept
Lorsqu'une particule dotée d'un rayon donné se déplace dans l'espace, elle occupe effectivement l'espace d'un cylindre avec le même rayon. Pour qu'une particule entre en collision avec une autre, la seconde doit avoir une partie de son volume à l'intérieur de ce cylindre. Dans le cas le plus extrême, la deuxième particule se trouve à une distance de deux rayons de la première, de sorte que le bord du cylindre touche un point de la sphère le plus proche de l'axe du cylindre. Le centre de cette sphère est situé à une distance égale à un rayon de la surface du cylindre :
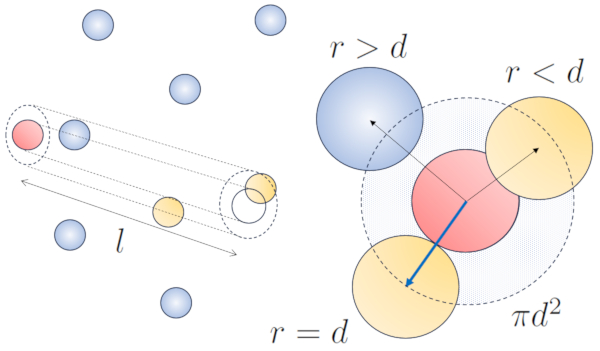
Par conséquent, la distance entre l'axe du cylindre et le centre de n'importe quelle particule est de deux rayons, autrement dit, un diamètre. En essence, on peut imaginer que le volume littéralement occupé par la particule se déplaçant dans l'espace est un cylindre ayant une longueur égale au libre parcours et un rayon égal au diamètre de la particule elle-même.
ID:(1962, 0)
Sentier libre avec circulation des voisins
Concept
Lorsque des particules voisines sont en mouvement, il existe une probabilité plus élevée de collision en raison du fait qu'elles parcourent une plus grande distance en même temps. Les composantes de vitesse, $v_x$, $v_y$ et $v_z$, fluctuent autour de valeurs moyennes $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ et $\sqrt{\langle v_z^2\rangle}$. En supposant que le système soit isotrope, la moyenne de chaque composante sera égale à $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Par conséquent, le long de l'axe le long duquel la particule se déplace, elle parcourra une distance
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
En même temps, les particules se déplaçant perpendiculairement auront parcouru une distance :
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Ainsi, la probabilité de collision augmente d'un facteur de $\sqrt{2}$ par rapport au cas où les particules ne sont pas en mouvement :
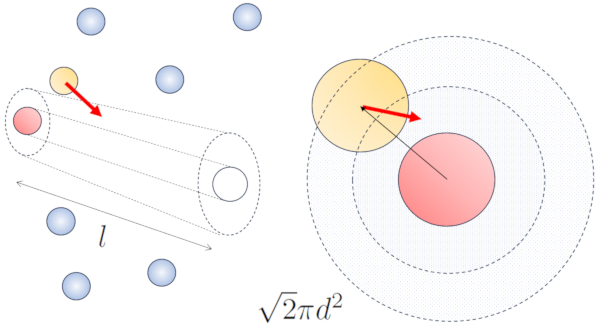
ID:(1963, 0)
Diffusion de particules
Concept
S'il existe une différence spatiale dans a concentration de particules ($c_n$), un phénomène connu sous le nom de variation des concentrations ($dc_n$) se produit. La probabilité que les particules atteignent une positionner le long d'un axe ($z$) à partir d'une position avant une distance de le route libre ($\bar{l}$) est différente de la probabilité à partir d'une position après la même distance. Cela conduit à des changements dans a concentration de particules ($c_n$), un processus connu sous le nom de diffusion. La vitesse à laquelle ce processus se produit est celle de a vitesse moyenne d'une particule ($\bar{v}$), et en elle, $1/6$ des particules participent dans chaque direction, car il y a un total de 6 directions dans un espace tridimensionnel.
De cette manière, a densité de flux de particules ($j$) est généré, qui en termes de superficie correspond à :
$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$
Les constantes qui sont factorisées lors du calcul de a densité de flux de particules ($j$) sont résumées en une constante appelée a constante de diffusion ($D$), qui est égale au tiers du produit de le route libre ($\bar{l}$) et a vitesse moyenne d'une particule ($\bar{v}$).
ID:(15143, 0)
Évaporation de l'eau dans la couche
Concept
Le calcul de a densité de flux de particules ($j$) en fonction de a variation des concentrations ($dc_n$), variation de position ($dz$) et a constante de diffusion ($D$) :
nous permet de déterminer comment l'eau s'évapore de la nappe phréatique. Pour ce faire, les étapes suivantes sont nécessaires :
• Obtenez la température ambiante, lhumidité relative, la porosité du sol et la profondeur de la nappe phréatique.
• Calculer la température de l'eau à la surface de la nappe phréatique.
• Calculer la concentration saturée de vapeur d'eau au-dessus de la nappe phréatique.
• Calculer la concentration de vapeur d'eau au-dessus du sol.
• Calculer le flux de vapeur d'eau pour la limite de flux stationnaire.
ID:(15145, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ c_m \equiv\displaystyle\frac{ n }{ V }$
c_m = n / V
$ c_n = N_A c_m $
c_n = N_A * c_m
$ c_n =\displaystyle\frac{ \rho }{ m }$
c_n = rho / m
$ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $
D = v * l /3
$ E =\displaystyle\frac{ f }{2} k_B T $
E = f * k_B * T /2
$ j =- D \displaystyle\frac{ dc_n }{ dz }$
j =- D * dc_n / dz
$ \vec{j} =- D \nabla c_n $
j =-D * nabla c_n
$ K =\displaystyle\frac{ m }{2} \bar{v} ^2$
K = m * v ^2/2
$ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$
l = 1/( d ^2 * pi * c )
$ m =\displaystyle\frac{ M_m }{ N_A }$
m = M_m / N_A
$ n = \displaystyle\frac{ M }{ M_m }$
n = M / M_m
$ n \equiv\displaystyle\frac{ N }{ N_A }$
n = N / N_A
$ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$
v =sqrt( f * k_B * T / m )
$\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$
@DIFF( c_n, t, 1) = @DIFF( D * @DIFF( c_n , z , 1), z , 1)
$l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$
l = 1 / ( sqrt(2) * pi * d^2 * c_n )
ID:(15232, 0)
Concentration molaire
Équation
A concentration molaire ($c_m$) correspond à nombre de taupes ($n$) divisé par le volume ($V$) d'un gaz et est calculé comme suit :
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
ID:(4878, 0)
Concentration molaire
Équation
Le nombre de taupes ($n$) correspond à Le nombre de particules ($N$) divisé par le numéro d'Avogadro ($N_A$) :
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
ID:(3748, 0)
Concentration de particules et de taupes
Équation
Pour convertir a concentration molaire ($c_m$) en a concentration de particules ($c_n$), il suffit de multiplier la première par le numéro d'Avogadro ($N_A$), comme suit :
| $ c_n = N_A c_m $ |
ID:(10624, 0)
Nombre de moles avec masse molaire
Équation
Le nombre de taupes ($n$) est déterminé en divisant a masse ($M$) d'une substance par son a masse molaire ($M_m$), ce qui correspond au poids d'une mole de la substance.
Par conséquent, la relation suivante peut être établie :
| $ n = \displaystyle\frac{ M }{ M_m }$ |
Le nombre de taupes ($n$) correspond à Le nombre de particules ($N$) divisé par le numéro d'Avogadro ($N_A$) :
Si nous multiplions à la fois le numérateur et le dénominateur par a masse molaire ($m$), nous obtenons :
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Donc, c'est :
La masse molaire est exprimée en grammes par mole (g/mol).
ID:(4854, 0)
Concentration basée sur la masse molaire
Équation
Si nous divisons a densité ($\rho$) par a masse molaire ($m$), nous obtiendrons a concentration de particules ($c_n$) :
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
Avec a concentration de particules ($c_n$) comme le nombre de particules ($N$) et le volume ($V$), nous obtenons :
| $ c_n \equiv \displaystyle\frac{ N }{ V }$ |
Avec a masse molaire ($m$) et a masse ($M$),
| $ m \equiv \displaystyle\frac{ M }{ N }$ |
Comme a densité ($\rho$) est
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
nous obtenons
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Ainsi,
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
ID:(10623, 0)
Libre parcours avec concentration de particules
Équation
La longueur libre moyenne peut être estimée en fonction du diamètre d'un cylindre imaginaire entourant une particule, en moyenne ayant une collision avec une autre particule.
Le rayon du cylindre correspond à la distance maximale que deux particules doivent avoir pour entrer en collision, ce qui équivaut à deux fois le rayon de la particule, c'est-à-dire le diamètre des particules ($d$). Comme seule une collision se produit à l'intérieur de ce cylindre, le nombre de particules qu'il contient doit être égal à un. Cela signifie que :
$l d^2\pi c_n= 1$
avec a concentration de particules ($c_n$), et en résolvant pour le route libre ($\bar{l}$), nous obtenons :
| $ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$ |
Cela représente la longueur libre moyenne.
ID:(4392, 0)
Route moyenne libre pour les voisins en mouvement
Équation
Dans le cas sans mouvement, la probabilité est de le route libre ($\bar{l}$), tandis qu'avec le mouvement, les probabilités sont de le diamètre des particules ($d$) et a concentration de particules ($c_n$), respectivement.
Dans le cas du mouvement, la probabilité augmente d'un facteur de $\sqrt{2}$, ce qui signifie que le chemin libre est
| $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)
Énergie cinétique de la particule
Équation
A énergie cinétique ($K$) en combinaison avec a masse molaire ($m$) et a vitesse moyenne d'une particule ($\bar{v}$) équivaut à
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
Remarque : Dans un strict respect des règles, l'énergie cinétique dépend de la moyenne de la vitesse au carré $\bar{v^2}$. Cependant, on suppose que cela est approximativement égal au carré de la moyenne de la vitesse :
$\bar{v^2}\sim\bar{v}^2$
ID:(4390, 0)
Masse des particules et masse molaire
Équation
A masse molaire ($m$) peut être estimé à partir de a masse molaire ($M_m$) et le numéro d'Avogadro ($N_A$) en utilisant
| $ m =\displaystyle\frac{ M_m }{ N_A }$ |
ID:(4389, 0)
Énergie basée sur les degrés de liberté
Équation
La loi de Stefan-Boltzmann, initialement proposée par Josef Stefan [1] et ensuite affinée par Ludwig Boltzmann [2], établit que a énergie d'une molécule ($E$) est proportionnelle à Le degrés de liberté ($f$) multipliée par a température absolue ($T$) avec une constante de proportionnalité de a constante de Boltzmann ($k_B$) :
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
Il est important de noter que a température absolue ($T$) doit être exprimée en degrés Kelvin.
Le nombre de degrés de liberté d'une particule correspond au nombre de variables nécessaires pour décrire son état thermodynamique. Par exemple, pour une particule ponctuelle, seules trois coordonnées sont nécessaires, ce qui donne lieu à trois degrés de liberté. Si la particule a une forme et une rigidité, deux angles supplémentaires sont nécessaires, ce qui entraîne un total de cinq degrés de liberté. Lorsque la particule peut se déformer ou vibrer dans une ou plusieurs directions, ces modes supplémentaires sont également considérés comme des degrés de liberté supplémentaires. Cependant, il est important de noter que ces degrés de liberté supplémentaires n'existent qu'à des températures élevées, lorsque la particule a suffisamment d'énergie pour activer de telles vibrations.
[1] "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur" (Sur la Relation entre le Rayonnement Thermique et la Température), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).
[2] "Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen" (Études Supplémentaires sur l'Équilibre Thermique entre les Molécules de Gaz), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).
ID:(4387, 0)
Constante de diffusion
Équation
La constante de diffusion $D$ peut être calculée à partir de la vitesse moyenne $\bar{v}$ et du libre parcours moyen $\bar{l}$ des particules.
| $ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $ |
Il est important de reconnaître que tant le libre parcours moyen que la vitesse moyenne dépendent de la température, et par conséquent, la constante de diffusion en dépend également. C'est pourquoi, lors de la publication de valeurs pour la prétendue constante, la température à laquelle elle s'applique est toujours spécifiée.
ID:(3186, 0)
L'équation de Fick en une dimension
Équation
En 1855, Adolf Fick [1] a formulé une équation pour le calcul de a constante de diffusion ($D$), ce qui conduit à A densité de flux de particules ($j$) en raison de a variation des concentrations ($dc_n$) le long de variation de position ($dz$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
[1] "Über Diffusion" (Sur la diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
ID:(4820, 0)
La loi de Fick dans plus de dimensions
Équation
A densité de flux de particules ($j$) en une dimension est calculé en utilisant les valeurs a constante de diffusion ($D$), a concentration de particules ($c_n$) et a positionner le long d'un axe ($z$), conformément à la loi de Fick [1] suivante:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Cette formule peut être généralisée pour plus d'une dimension comme suit :
| $ \vec{j} =- D \nabla c_n $ |
[1] "Über Diffusion" (Sur la diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
ID:(4821, 0)
Équation de diffusion des particules
Équation
Si a constante de diffusion ($D$) est égal à A densité de flux de particules ($j$) en raison de a variation des concentrations ($dc_n$) le long de variation de position ($dz$), cela est régi par la loi de Fick [1] :
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Par conséquent, pour décrire la variation de la concentration à Le temps ($t$), correspondant à la variation spatiale de la densité de flux, nous obtenons l'équation suivante :
| $\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$ |
[1] "Über Diffusion" (Sur la Diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855).
ID:(15144, 0)