Benützer:
Wasserdampfdiffusion im Boden
Storyboard 
Wenn die Konzentration nicht gleichmäßig ist, beginnen Diffusionsprozesse, bei denen sich der Wasserdampf aus Bereichen größerer oder geringerer Konzentration bewegt.
ID:(376, 0)
Freie Weglänge in einem Gas
Konzept
Wenn sich ein Teilchen eines Gases bewegt, interagiert es mit anderen Teilchen. Die einfachste Form dieser Interaktion erfolgt durch elastische Stöße, was bedeutet, dass das Teilchen ohne Energieverlust kollidiert und seine Richtung ändert, um ein anderes Teilchen zu treffen.
Im Rahmen dieses Prozesses macht es Sinn, der Freier Weg ($\bar{l}$) zu definieren, dessen Wert von ($$) abhängen wird.
ID:(1708, 0)
Freie Weglänge mit Nachbarn ohne Bewegung
Konzept
Wenn ein Teilchen mit einem gegebenen Radius sich im Raum bewegt, nimmt es effektiv den Raum eines Zylinders mit dem gleichen Radius ein. Damit ein Teilchen mit einem anderen kollidiert, muss sich dieses zweite Teilchen teilweise innerhalb dieses Zylinders befinden. Im extremsten Fall befindet sich das zweite Teilchen in einem Abstand von zwei Radien vom ersten Teilchen, so dass die Kante des Zylinders einen Punkt auf der Kugel berührt, der dem Zylinderachsen am nächsten liegt. Das Zentrum dieser Kugel ist einen Radius entfernt von der Oberfläche des Zylinders:
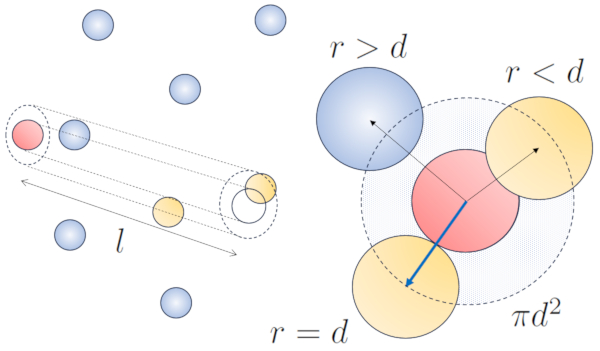
None
Daher beträgt der Abstand zwischen der Achse des Zylinders und dem Zentrum eines beliebigen Teilchens zwei Radien, oder anders ausgedrückt, ein Durchmesser. Im Wesentlichen kann man sich vorstellen, dass das tatsächlich vom sich durch den Raum bewegenden Teilchen eingenommene Volumen einem Zylinder mit einer Länge entspricht, die dem freien Weg entspricht, und einem Radius, der dem Durchmesser des Teilchens entspricht.
ID:(1962, 0)
Freie Weglänge mit Nachbarn mit Bewegung
Konzept
Wenn benachbarte Teilchen sich bewegen, besteht eine höhere Wahrscheinlichkeit für Kollisionen, da sie in derselben Zeitspanne eine größere Strecke zurücklegen. Die Geschwindigkeitskomponenten $v_x$, $v_y$ und $v_z$ schwanken um Mittelwerte von $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ und $\sqrt{\langle v_z^2\rangle}$. Unter der Annahme, dass das System isotrop ist, wird der Durchschnitt jeder Komponente gleich $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$ sein. Daher wird entlang der Achse, entlang der die Partikel sich bewegen, eine Strecke zurückgelegt
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
Zur gleichen Zeit haben Teilchen, die sich senkrecht bewegen, eine Strecke zurückgelegt:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Daher erhöht sich die Wahrscheinlichkeit einer Kollision um den Faktor $\sqrt{2}$ im Vergleich zum Fall, in dem sich die Partikel nicht bewegen:
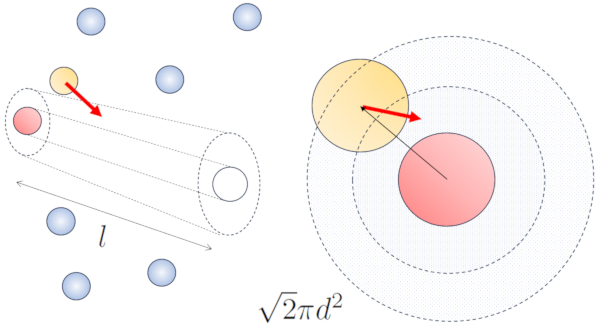
None
ID:(1963, 0)
Partikeldiffusion
Konzept
Wenn es einen räumlichen Unterschied in die Partikelkonzentration ($c_n$) gibt, tritt ein Phänomen auf, das als Konzentrationsvariation ($dc_n$) bekannt ist. Die Wahrscheinlichkeit, dass Teilchen von einer Position vor einer Entfernung von der Freier Weg ($\bar{l}$) zu eine Positionieren Sie entlang einer Achse ($z$) gelangen, unterscheidet sich von der Wahrscheinlichkeit von einer Position nach derselben Entfernung. Dies führt zu Veränderungen in die Partikelkonzentration ($c_n$), einem Prozess, der als Diffusion bekannt ist. Die Geschwindigkeit, mit der dieser Prozess stattfindet, ist die von die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$), und daran beteiligen sich jeweils $1/6$ der Partikel in jede Richtung, da es insgesamt 6 Richtungen in einem dreidimensionalen Raum gibt.
None
Auf diese Weise wird die Teilchenflussdichte ($j$) generiert, das in Bezug auf die Fläche folgendermaßen entspricht:
$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$
Die Konstanten, die beim Berechnen von die Teilchenflussdichte ($j$) faktorisiert werden, werden in einer Konstanten zusammengefasst, die als die Diffusionskonstante ($D$) bezeichnet wird und gleich einem Drittel des Produkts von der Freier Weg ($\bar{l}$) und die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$) ist.
ID:(15143, 0)
Verdunstung von Wasser in der Schicht
Konzept
Die Berechnung von die Teilchenflussdichte ($j$) basierend auf die Konzentrationsvariation ($dc_n$), Positionsvariation ($dz$) und die Diffusionskonstante ($D$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
ermöglicht es uns, zu bestimmen, wie Wasser aus dem Grundwasserspiegel verdunstet. Dazu sind folgende Schritte erforderlich:
• Die Umgebungstemperatur, relative Luftfeuchtigkeit, Bodenporosität und die Tiefe des Grundwasserspiegels ermitteln.
• Die Wassertemperatur an der Oberfläche des Grundwasserspiegels berechnen.
• Die gesättigte Wasserdampfkonzentration über dem Grundwasserspiegel berechnen.
• Die Wasserdampfkonzentration über dem Boden berechnen.
• Den Wasserdampffluss für die stationäre Fließgrenze berechnen.
ID:(15145, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ c_m \equiv\displaystyle\frac{ n }{ V }$
c_m = n / V
$ c_n = N_A c_m $
c_n = N_A * c_m
$ c_n =\displaystyle\frac{ \rho }{ m }$
c_n = rho / m
$ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $
D = v * l /3
$ E =\displaystyle\frac{ f }{2} k_B T $
E = f * k_B * T /2
$ j =- D \displaystyle\frac{ dc_n }{ dz }$
j =- D * dc_n / dz
$ \vec{j} =- D \nabla c_n $
j =-D * nabla c_n
$ K =\displaystyle\frac{ m }{2} \bar{v} ^2$
K = m * v ^2/2
$ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$
l = 1/( d ^2 * pi * c )
$ m =\displaystyle\frac{ M_m }{ N_A }$
m = M_m / N_A
$ n = \displaystyle\frac{ M }{ M_m }$
n = M / M_m
$ n \equiv\displaystyle\frac{ N }{ N_A }$
n = N / N_A
$ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$
v =sqrt( f * k_B * T / m )
$\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$
@DIFF( c_n, t, 1) = @DIFF( D * @DIFF( c_n , z , 1), z , 1)
$l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$
l = 1 / ( sqrt(2) * pi * d^2 * c_n )
ID:(15232, 0)
Molare Konzentration
Gleichung
Die Molare Konzentration ($c_m$) entspricht Anzahl der Mol ($n$) geteilt durch der Volumen ($V$) eines Gases und wird wie folgt berechnet:
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
ID:(4878, 0)
Anzahl der Mole
Gleichung
Der Anzahl der Mol ($n$) entspricht der Anzahl der Partikel ($N$) geteilt durch der Avogadros Nummer ($N_A$):
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
ID:(3748, 0)
Partikel- und Molkonzentration
Gleichung
Um die Molare Konzentration ($c_m$) in die Partikelkonzentration ($c_n$) umzuwandeln, multiplizieren Sie einfach die erste Zahl mit der Avogadros Nummer ($N_A$), wie folgt:
| $ c_n = N_A c_m $ |
ID:(10624, 0)
Anzahl der Mol mit Molmasse
Gleichung
Der Anzahl der Mol ($n$) wird ermittelt, indem man die Masse ($M$) einer Substanz durch ihr die Molmasse ($M_m$) teilt, was dem Gewicht eines Mols der Substanz entspricht.
Daher kann die folgende Beziehung hergestellt werden:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
Der Anzahl der Mol ($n$) entspricht der Anzahl der Partikel ($N$) geteilt durch der Avogadros Nummer ($N_A$):
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
Wenn wir sowohl den Zähler als auch den Nenner mit die Partikelmasse ($m$) multiplizieren, erhalten wir:
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Also ist es:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
Die molare Masse wird in Gramm pro Mol (g/mol) ausgedrückt.
ID:(4854, 0)
Konzentration bezogen auf die Molmasse
Gleichung
Wenn wir die Dichte ($\rho$) durch die Partikelmasse ($m$) teilen, erhalten wir die Partikelkonzentration ($c_n$):
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
Mit die Partikelkonzentration ($c_n$) als der Anzahl der Partikel ($N$) und der Volumen ($V$) erhalten wir:
| $ c_n \equiv \displaystyle\frac{ N }{ V }$ |
Mit die Partikelmasse ($m$) und die Masse ($M$),
| $ m \equiv \displaystyle\frac{ M }{ N }$ |
Da die Dichte ($\rho$) ist
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
erhalten wir
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Deshalb,
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
ID:(10623, 0)
Freier Weg mit Partikelkonzentration
Gleichung
Der mittlere freie Weg kann in Abhängigkeit vom Durchmesser eines imaginären Zylinders geschätzt werden, der eine Partikel umgibt und im Durchschnitt eine Kollision mit einer anderen Partikel hat.
Der Radius des Zylinders entspricht dem maximalen Abstand, den zwei Partikel haben müssen, um zu kollidieren, was dem doppelten Radius der Partikel entspricht, d.h. Der Partikeldurchmesser ($d$). Da innerhalb dieses Zylinders nur eine Kollision stattfindet, muss die Anzahl der darin enthaltenen Partikel gleich eins sein. Das bedeutet:
$l d^2\pi c_n= 1$
mit die Partikelkonzentration ($c_n$), und wenn wir nach der Freier Weg ($\bar{l}$) auflösen, erhalten wir:
| $ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$ |
Dies stellt den mittleren freien Weg dar.
ID:(4392, 0)
Mittlere Freie Weglänge für Bewegte Nachbaren
Gleichung
Für den Fall ohne Bewegung beträgt die Wahrscheinlichkeit der Freier Weg ($\bar{l}$), während sie sich bei Bewegung auf der Partikeldurchmesser ($d$) und die Partikelkonzentration ($c_n$) ändert.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
Im Fall der Bewegung steigt die Wahrscheinlichkeit um den Faktor $\sqrt{2}$, was bedeutet, dass der freie Weg beträgt
| $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)
Kinetische Energie des Teilchens
Gleichung
Die Kinetische Energie ($K$) in Kombination mit die Partikelmasse ($m$) und die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$) ergibt
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
Hinweis: In strengerem Sinne hängt die kinetische Energie vom Durchschnitt der Geschwindigkeit zum Quadrat $\bar{v^2}$ ab. Es wird jedoch angenommen, dass dies ungefähr gleich dem Quadrat des Durchschnitts der Geschwindigkeit ist:
$\bar{v^2}\sim\bar{v}^2$
ID:(4390, 0)
Teilchenmasse und Molmasse
Gleichung
Die Partikelmasse ($m$) kann aus die Molmasse ($M_m$) und der Avogadros Nummer ($N_A$) geschätzt werden mithilfe von
| $ m =\displaystyle\frac{ M_m }{ N_A }$ |
ID:(4389, 0)
Energie als Funktion der Freiheitsgrade
Gleichung
Das Stefan-Boltzmann-Gesetz, das ursprünglich von Josef Stefan [1] formuliert und später von Ludwig Boltzmann [2] weiterentwickelt wurde, besagt, dass die Energie eines Moleküls ($E$) proportional zu das Freiheitsgrade ($f$) multipliziert mit die Absolute Temperatur ($T$) ist, wobei eine Proportionalitätskonstante von die Boltzmann-Konstante ($k_B$) vorliegt:
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
Es ist wichtig zu beachten, dass die Absolute Temperatur ($T$) unbedingt in Kelvin ausgedrückt werden muss.
Die Anzahl der Freiheitsgrade eines Teilchens entspricht der Anzahl der Variablen, die erforderlich sind, um seinen thermodynamischen Zustand zu beschreiben. Zum Beispiel benötigt ein Punktteilchen nur drei Koordinaten, was zu drei Freiheitsgraden führt. Wenn das Teilchen jedoch eine Form und Steifigkeit aufweist, sind zwei zusätzliche Winkel erforderlich, was zu insgesamt fünf Freiheitsgraden führt. Wenn das Teilchen sich zusätzlich deformieren oder in einer oder mehreren Richtungen schwingen kann, werden diese zusätzlichen Modi ebenfalls als zusätzliche Freiheitsgrade betrachtet. Es ist jedoch wichtig zu beachten, dass diese zusätzlichen Freiheitsgrade nur bei hohen Temperaturen existieren, wenn das Teilchen genügend Energie hat, um solche Schwingungen zu aktivieren.
[1] "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur" (Über die Beziehung zwischen der Wärmestrahlung und der Temperatur), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).
[2] "Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen" (Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).
ID:(4387, 0)
Durchschnittliche Teilchengeschwindigkeit
Gleichung
Como la energía cinética de la molécula es
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
y la energía en función de la temperatura es
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
con
| $ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$ |
ID:(4391, 0)
Diffusionskonstante
Gleichung
Die Diffusionskonstante $D$ kann aus der durchschnittlichen Geschwindigkeit $\bar{v}$ und dem mittleren freien Weg $\bar{l}$ der Teilchen berechnet werden.
| $ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $ |
Es ist wichtig zu erkennen, dass sowohl der mittlere freie Weg als auch die Durchschnittsgeschwindigkeit von der Temperatur abhängen, und folglich auch die Diffusionskonstante. Daher wird bei der Veröffentlichung von Werten für die sogenannte Konstante immer die Temperatur angegeben, auf die sie sich bezieht.
ID:(3186, 0)
Ficks Gesetz in einer Dimension
Gleichung
Im Jahr 1855 formulierte Adolf Fick [1] eine Gleichung zur Berechnung von die Diffusionskonstante ($D$), was zu die Teilchenflussdichte ($j$) aufgrund von die Konzentrationsvariation ($dc_n$) entlang Positionsvariation ($dz$) führt:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
[1] "Über Diffusion", Adolf Fick, Annalen der Physik und Chemie, Band 170, Seiten 59-86 (1855)
ID:(4820, 0)
Ficks Gesetz in mehr Dimensionen
Gleichung
In einer Dimension wird die Teilchenflussdichte ($j$) unter Verwendung der Werte die Diffusionskonstante ($D$), die Partikelkonzentration ($c_n$) und die Positionieren Sie entlang einer Achse ($z$) gemäß dem Fickschen Gesetz [1] berechnet:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Diese Formel kann für mehr als eine Dimension verallgemeinert werden wie folgt:
| $ \vec{j} =- D \nabla c_n $ |
[1] "Über Diffusion", Adolf Fick, Annalen der Physik und Chemie, Band 170, Seiten 59-86 (1855)
ID:(4821, 0)
Teilchendiffusionsgleichung
Gleichung
Wenn die Diffusionskonstante ($D$) gleich die Teilchenflussdichte ($j$) ist aufgrund von die Konzentrationsvariation ($dc_n$) entlang Positionsvariation ($dz$), wird dies durch das Gesetz von Fick [1] geregelt:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Daher erhalten wir zur Beschreibung der Konzentrationsänderung bei der Zeit ($t$), die der räumlichen Änderung der Flussdichte entspricht, die Gleichung
| $\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$ |
[1] "Über Diffusion" (Über Diffusion), Adolf Fick, Annalen der Physik und Chemie, Band 170, Seiten 59-86 (1855).
ID:(15144, 0)