User:
Water Vapor Diffusion in the Soil
Storyboard 
When the concentration is not uniform, diffusion processes begin with which the water vapor moves from areas of greater or lesser concentration.
ID:(376, 0)
Free path in a gas
Concept
When a particle of a gas moves, it interacts with other particles. The simplest form of this interaction is through elastic collisions, meaning that the particle collides without losing energy, changing its direction to impact another particle.
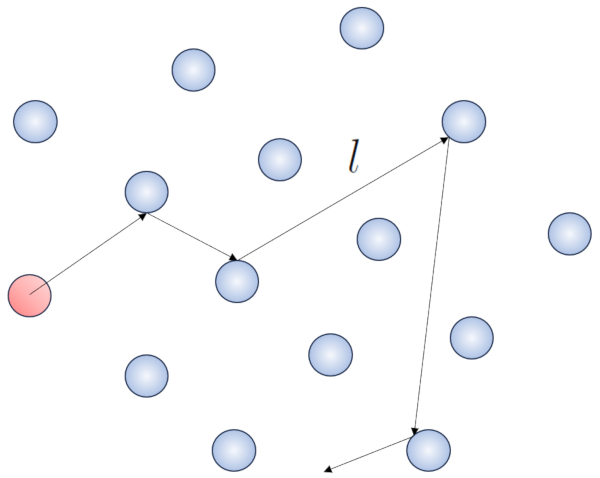
None
Within this process, it makes sense to define the free path ($\bar{l}$), whose value will depend on ($$).
ID:(1708, 0)
Free path with neighbors without movement
Concept
When a particle with a given radius moves through space, it effectively occupies the space of a cylinder with the same radius. For one particle to collide with another, the second particle must have some of its volume within this cylinder. In the most extreme case, the second particle is located at a distance of two radii from the first one, so that the edge of the cylinder touches a point on the sphere closest to the cylinder's axis. The center of this sphere is at a distance equal to one radius from the surface of the cylinder:
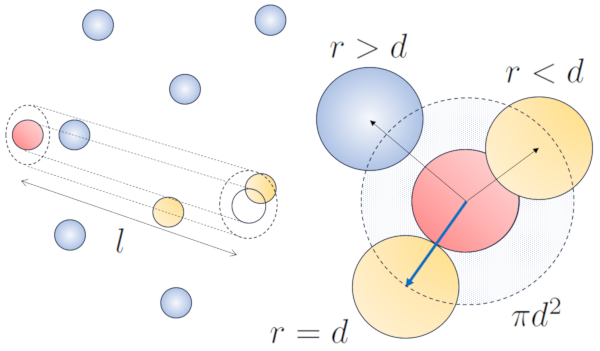
None
Therefore, the distance between the cylinder's axis and the center of any particle is two radii, or in other words, a diameter. In essence, one can imagine that the volume literally occupied by the particle traveling through space is a cylinder with a length equal to the free path and a radius equal to the particle's diameter.
ID:(1962, 0)
Free path with neighbors with movement
Concept
When neighboring particles are in motion, there is a higher probability of collision due to the fact that they cover a greater distance in the same amount of time. The velocity components, $v_x$, $v_y$, and $v_z$, fluctuate around mean values $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$, and $\sqrt{\langle v_z^2\rangle}$. Assuming the system is isotropic, the average of each component will be equal to $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Therefore, along the axis along which the particle is moving, it will travel a distance
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
At the same time, particles moving perpendicular will have covered a distance:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Hence, the collision probability increases by a factor of $\sqrt{2}$ compared to the case where the particles are not in motion:
None
ID:(1963, 0)
Particle diffusion
Concept
If there is a spatial difference in the particle concentration ($c_n$), a phenomenon known as concentration variation ($dc_n$) occurs. The probability of particles reaching a position along an axis ($z$) from a position before a distance of the free path ($\bar{l}$) is different from the probability from a position after the same distance. This leads to changes in the particle concentration ($c_n$), a process known as diffusion. The speed at which this process occurs is that of the average speed of a particle ($\bar{v}$), and in it, $1/6$ of the particles participate in each direction, as there are a total of 6 directions in a three-dimensional space.
None
In this way, the particle flux density ($j$) is generated, which in terms of area corresponds to:
$j=\displaystyle\frac{1}{6}\bar{v}c(z-\bar{l}) - \displaystyle\frac{1}{6}\bar{v}c(z+\bar{l})=\displaystyle\frac{1}{6}\bar{v}[c(z-\bar{l})-c(z+\bar{l})]=-\displaystyle\frac{1}{6}\bar{v}2\bar{l}\displaystyle\frac{dc}{dz}$
The constants that are factored in when calculating the particle flux density ($j$) are summarized into a constant called the diffusion Constant ($D$), which is equal to one-third of the product of the free path ($\bar{l}$) and the average speed of a particle ($\bar{v}$).
ID:(15143, 0)
Evaporation of water in the layer
Concept
Calculating the particle flux density ($j$) based on the concentration variation ($dc_n$), position variation ($dz$), and the diffusion Constant ($D$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
allows us to determine how water evaporates from the water table. To do this, the following steps are required:
• Obtain ambient temperature, relative humidity, soil porosity and depth of the water table.
• Calculate the water temperature at the water table surface.
• Calculate the saturated vapor concentration above the water table.
• Calculate the vapor concentration above the soil.
• Calculate the water vapor flux for the steady-state flow boundary.
ID:(15145, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ c_m \equiv\displaystyle\frac{ n }{ V }$
c_m = n / V
$ c_n = N_A c_m $
c_n = N_A * c_m
$ c_n =\displaystyle\frac{ \rho }{ m }$
c_n = rho / m
$ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $
D = v * l /3
$ E =\displaystyle\frac{ f }{2} k_B T $
E = f * k_B * T /2
$ j =- D \displaystyle\frac{ dc_n }{ dz }$
j =- D * dc_n / dz
$ \vec{j} =- D \nabla c_n $
j =-D * nabla c_n
$ K =\displaystyle\frac{ m }{2} \bar{v} ^2$
K = m * v ^2/2
$ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$
l = 1/( d ^2 * pi * c )
$ m =\displaystyle\frac{ M_m }{ N_A }$
m = M_m / N_A
$ n = \displaystyle\frac{ M }{ M_m }$
n = M / M_m
$ n \equiv\displaystyle\frac{ N }{ N_A }$
n = N / N_A
$ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$
v =sqrt( f * k_B * T / m )
$\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$
@DIFF( c_n, t, 1) = @DIFF( D * @DIFF( c_n , z , 1), z , 1)
$l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$
l = 1 / ( sqrt(2) * pi * d^2 * c_n )
ID:(15232, 0)
Molar concentration
Equation
The molar concentration ($c_m$) corresponds to number of moles ($n$) divided by the volume ($V$) of a gas and is calculated as follows:
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
ID:(4878, 0)
Number of moles
Equation
The number of moles ($n$) corresponds to the number of particles ($N$) divided by the avogadro's number ($N_A$):
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
ID:(3748, 0)
Particle and mole concentration
Equation
To convert the molar concentration ($c_m$) to the particle concentration ($c_n$), simply multiply the former by the avogadro's number ($N_A$) as follows:
| $ c_n = N_A c_m $ |
ID:(10624, 0)
Number of moles with molar mass
Equation
The number of moles ($n$) is determined by dividing the mass ($M$) of a substance by its the molar Mass ($M_m$), which corresponds to the weight of one mole of the substance.
Therefore, the following relationship can be established:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
The number of moles ($n$) corresponds to the number of particles ($N$) divided by the avogadro's number ($N_A$):
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
If we multiply both the numerator and the denominator by the particle mass ($m$), we obtain:
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
So it is:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
The molar mass is expressed in grams per mole (g/mol).
ID:(4854, 0)
Concentration based on molar mass
Equation
If we divide the density ($\rho$) by the particle mass ($m$), we will obtain the particle concentration ($c_n$):
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
Given the particle concentration ($c_n$) with the number of particles ($N$) and the volume ($V$), we have:
| $ c_n \equiv \displaystyle\frac{ N }{ V }$ |
With the particle mass ($m$) and the mass ($M$),
| $ m \equiv \displaystyle\frac{ M }{ N }$ |
As the density ($\rho$) is
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
we obtain
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Therefore,
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
ID:(10623, 0)
Free path with particle concentration
Equation
The mean free path can be estimated in terms of the diameter of an imaginary cylinder surrounding a particle, on average having one collision with another particle.
The radius of the cylinder corresponds to the maximum distance two particles must have to collide, which is equal to twice the radius of the particle, i.e., the particle diameter ($d$). Since only one collision occurs within this cylinder, the number of particles contained within it must be equal to one. This means that:
$l d^2\pi c_n= 1$
with the particle concentration ($c_n$), and solving for the free path ($\bar{l}$), we obtain:
| $ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$ |
This represents the mean free path.
ID:(4392, 0)
Mean free path for moving neighbors
Equation
For the case without movement, the probability is the free path ($\bar{l}$), whereas with movement, the probabilities are the particle diameter ($d$) and the particle concentration ($c_n$), respectively.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
In the case of movement, the probability increases by a factor of $\sqrt{2}$, which means the free path is
| $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)
Kinetic energy of the particle
Equation
The kinetic energy ($K$) combined with the particle mass ($m$) and the average speed of a particle ($\bar{v}$) equals
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
Note: In strict rigor, kinetic energy depends on the average velocity squared $\bar{v^2}$. However, it is assumed to be approximately equal to the square of the average velocity:
$\bar{v^2}\sim\bar{v}^2$
ID:(4390, 0)
Particle mass and molar mass
Equation
The particle mass ($m$) can be estimated from the molar Mass ($M_m$) and the avogadro's number ($N_A$) using
| $ m =\displaystyle\frac{ M_m }{ N_A }$ |
ID:(4389, 0)
Energy as a function of degrees of freedom
Equation
The Stefan-Boltzmann law, initially proposed by Josef Stefan [1] and later refined by Ludwig Boltzmann [2], states that the energy of a molecule ($E$) is proportional to the degrees of freedom ($f$) multiplied by the absolute temperature ($T$) with a proportionality constant of the boltzmann Constant ($k_B$):
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
It is important to note that the absolute temperature ($T$) must be expressed in degrees Kelvin.
The number of degrees of freedom of a particle corresponds to the number of variables required to describe its thermodynamic state. For instance, a point particle requires only three coordinates, resulting in three degrees of freedom. If the particle has shape and rigidity, two additional angles are needed, leading to a total of five degrees of freedom. When the particle can deform or vibrate in one or more directions, these additional modes are also considered as additional degrees of freedom. However, it is important to note that these extra degrees of freedom exist only at high temperatures when the particle has enough energy to activate such vibrations.
[1] "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur" (On the Relationship Between Heat Radiation and Temperature), Josef Stefan, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1879).
[2] "Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen" (Further Studies on Thermal Equilibrium among Gas Molecules), Ludwig Boltzmann, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften, Wien (1884).
ID:(4387, 0)
Average speed of particles
Equation
Como la energía cinética de la molécula es
| $ K =\displaystyle\frac{ m }{2} \bar{v} ^2$ |
y la energía en función de la temperatura es
| $ E =\displaystyle\frac{ f }{2} k_B T $ |
con
| $ \bar{v} =\sqrt{\displaystyle\frac{ f k_B T }{ m }}$ |
ID:(4391, 0)
Diffusion constant
Equation
The diffusion constant $D$ can be calculated from the average velocity $\bar{v}$ and the mean free path $\bar{l}$ of the particles.
| $ D =\displaystyle\frac{1}{3} \bar{v} \bar{l} $ |
It is important to recognize that both the mean free path and the average velocity depend on temperature, and consequently, so does the diffusion constant. Therefore, when values for the so-called constant are published, the temperature to which it applies is always specified.
ID:(3186, 0)
Fick's law in one dimension
Equation
In 1855, Adolf Fick [1] formulated an equation for the calculation of the diffusion Constant ($D$), resulting in the particle flux density ($j$) due to the concentration variation ($dc_n$) along position variation ($dz$):
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
[1] "Über Diffusion" (On Diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
ID:(4820, 0)
Fick's law in more dimensions
Equation
Calculating the particle flux density ($j$) in one dimension involves utilizing the values the diffusion Constant ($D$), the particle concentration ($c_n$), and the position along an axis ($z$), as dictated by Fick's law [1]::
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
This formula can be generalized for more than one dimension as follows:
| $ \vec{j} =- D \nabla c_n $ |
[1] "Über Diffusion" (On Diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855)
ID:(4821, 0)
Particle diffusion equation
Equation
If the diffusion Constant ($D$) equals the particle flux density ($j$) due to the concentration variation ($dc_n$) along position variation ($dz$), this is governed by Fick's law [1]:
| $ j =- D \displaystyle\frac{ dc_n }{ dz }$ |
Therefore, to describe the variation in concentration at the time ($t$), which corresponds to the spatial variation of flux density, we obtain the equation
| $\displaystyle\frac{\partial c_n}{\partial t } = \displaystyle\frac{ \partial }{ \partial z }\left( D \displaystyle\frac{ \partial c_n }{ \partial z }\right)$ |
[1] "Über Diffusion" (On Diffusion), Adolf Fick, Annalen der Physik und Chemie, Volume 170, pages 59-86 (1855).
ID:(15144, 0)