User:


Period forecast
Storyboard

Once the similar segment has been determined, the data that follows it can be obtained.

With the way the magnitude varies, it can be estimated how the climatic parameter should continue after the current segment.

If the analysis is carried out with a reference segment from the recent past, in which actual posterior data exists, these can be compared with the forecast.

In this way, the forecast error can be estimated.

>Model

ID:(1914, 0)


Complex version of the Fourier series
Equation

>Top, >Model


Fourier transform

$ x(t) = \displaystyle\sum_{k=-\infty}^{\infty}( a_k \cos 2 \pi \nu_k t + b_k \sin 2 \pi \nu_k t )$



you can with Euler\'s relation



the definition

$ X_k = a_k - i b_k $



and the decreticization of time

$ t_n = n \Delta t $



redefine as the discrete transforms on the complex space of the time series x_n equal to

$ x_n = \displaystyle\sum_{k=0}^{N-1} X_k e^{ i 2 \pi \nu_k n \Delta t }$

ID:(14351, 0)


Forecast chart
Image

>Top


Si se grafica la función calculada en los 36 meses posteriores al tiempo en que se calcularon los modos se obtiene un pronostico para el parametro:

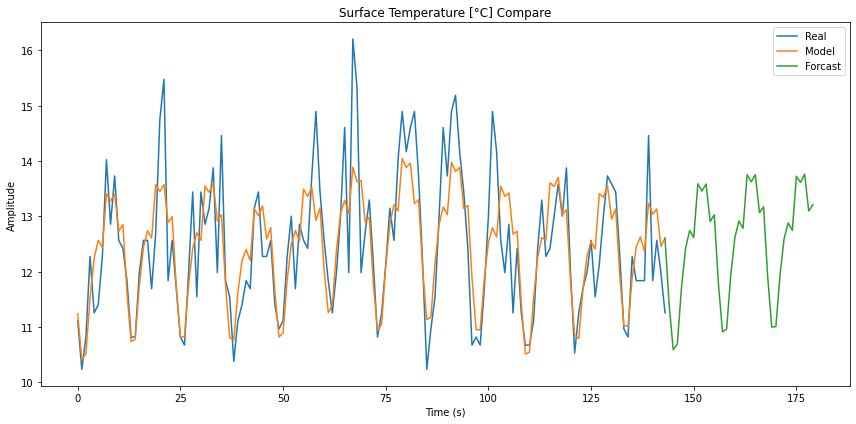
ID:(14358, 0)


Overall error
Equation

>Top, >Model


La eliminación de las fluctuaciones conlleva a un error inherente al método. Para estimarlo se puede directamente comparar el valor real con el estimado sin la fluctuación. Para ello se puede obtener el promedio de la diferencia dividido por el valor medio:

$\epsilon = 2 \displaystyle\sum_n\displaystyle\frac{\mid x_n - \bar{x}_n\mid}{\mid x_n + \bar{x}_n\mid}$



Esto se puede calcular con el código

cnt0 = 0
err0 = 0
for i in range(len(x)):
    if Xm[i] + x[i] != 0:
        err0 = err0 + 2*abs(Xm[i] - x[i])/(Xm[i] + x[i])
        cnt0 = cnt0 + 1
        
err0 = err0/cnt0

donde x es el valor real y Xm aquel en que no se incluye la fluctuación.

ID:(14359, 0)


Forecast error
Concept

>Top


Si se reserva el ultimo año para evaluar el error y se calculan los modos con las 12 años anteriores. Con dichos modos se puede realizar un pronostico para los 12 meses que se reservaron y compararlo con los datos reales. De esta forma se puede estimar la calidad del pronostico para datos ya ocurridos que no se empelaron para el proceso de modelar.

ID:(14360, 0)