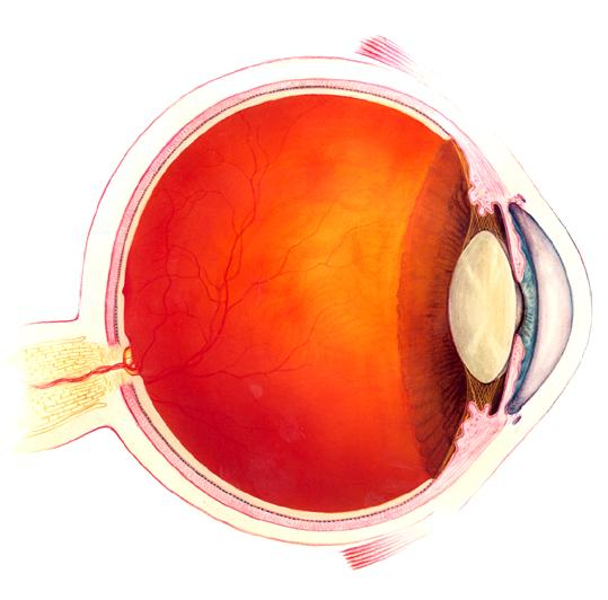
Auge
Beschreibung 
Das Auge besteht aus drei Schlüsselelementen, um das Licht nutzen zu können:
- Die Linse, die das Licht einstellt, darüber mehr im Bereich auf den Linsen
- das System, das Licht registriert und das Nervensystem, das Informationen zum Gehirn transportiert
- Das Gehirn, das die empfangenen Informationen verarbeitet
In diesem Abschnitt werden wir uns dem letzten Punkt widmen, da es der Punkt ist, der definiert, was unser Auge erfasst.
ID:(218, 0)
Sehen
Beschreibung 
Es gibt zwei Schlüsselaspekte in der Art, wie wir sehen.
Auf der einen Seite ist der Mechanismus, wie wir segmentieren, was wir in mehreren Teilfeldern sehen, die wir einzeln analysieren. Diese Analyse konzentriert sich dann auf die Erkennung bekannter Muster.
Zweitens gibt es unsere Fähigkeit, die Objekte in jedem dieser Teilfelder zu erkennen. Dies erfordert, ein Objekt und seine räumliche Position erkennen zu können.
ID:(488, 0)
Augenlinsen
Beschreibung 
Unser Auge ist in der Lage, die Brennweite des Objektivs einzustellen und dadurch Objekte in einem sehr großen Entfernungsbereich zu fokussieren.
Falls das Objektiv den Fokus in diesem Bereich nicht anpassen kann, können optische Linsen verwendet werden, die den Bereich modifizieren, der es fokussieren kann.
ID:(490, 0)
Position und Fokus von einer Konvexen Linse
Gleichung 
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}
Con la relación de similitud de los triángulos
| \displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} } |
se puede mostrar que se cumple:
| \displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} } |
ID:(3347, 0)
Proportionen der Größe und Position von einer konkaven Linse
Gleichung 
Für jedes Objektiv können Sie charakteristische Strahlen zeichnen, mit denen Sie auf ähnliche Weise zeigen können, dass die Größen des Objekts und des Bildes im gleichen Verhältnis stehen wie ihre Abstände zum optischen Element (Objektiv oder Spiegel).
Wenn das Objekt eine Größe
ID:(3346, 0)