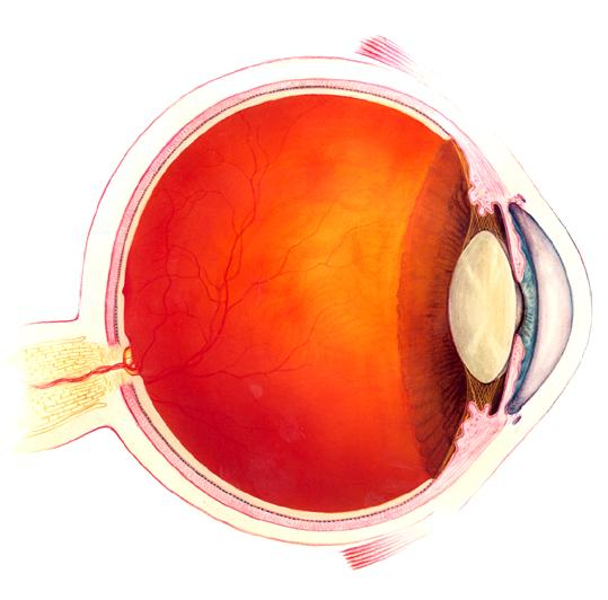
Ojo
Descripción 
El ojo esta constituido por tres elementos claves para poder aprovechar la luz:
- el lente que adapta la luz, sobre esto más en la sección sobre lentes
- el sistema que registra la luz y el sistema nervioso que lleva la información al cerebro
- el cerebro que procesa la información recibida
En esta sección nos dedicaremos al ultimo punto, ya que es el punto que define que capta nuestro ojo.
ID:(218, 0)
Ver
Descripción 
Existen dos aspectos claves en la forma como vemos.
Por un lado esta el mecanismo como segmentamos lo que vemos en múltiples sub-campos que analizamos en forma individual. Dicho análisis luego se centra en reconocer patrones conocidos.
En segunda instancia esta nuestra capacidad de reconocer los objetos en cada uno de estos sub-campos. Esto requiere de poder reconocer un objeto y su posición espacial.
ID:(488, 0)
Lentes del ojo
Descripción 
Nuestro ojo es capaz de ajustar la distancia focal del cristalino y con ello enfocar objetos en un rango muy amplio de distancias.
En caso de que el cristalino no es capaz de adecuar el foco en dicho rango se pueden emplear lentes ópticos que modifican el rango que es capaz de enfocar éste.
ID:(490, 0)
Posición y foco de lentes concavos
Ecuación 
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}
Con la relación de similitud de los triángulos
| \displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} } |
se puede mostrar que se cumple:
| \displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} } |
ID:(3347, 0)
Proporciones de tamaño y posición de lentes concavos
Ecuación 
Para cualquier lente se puede dibujar haces característicos con los cuales se puede por similitud mostrar que los tamaños del objeto y la imagen están en la misma proporción que sus distancias hasta el elemento óptico (lente o espejo).
Si el objeto tiene un tamaño
ID:(3346, 0)