Benützer:
Multiples lentes
Bild 
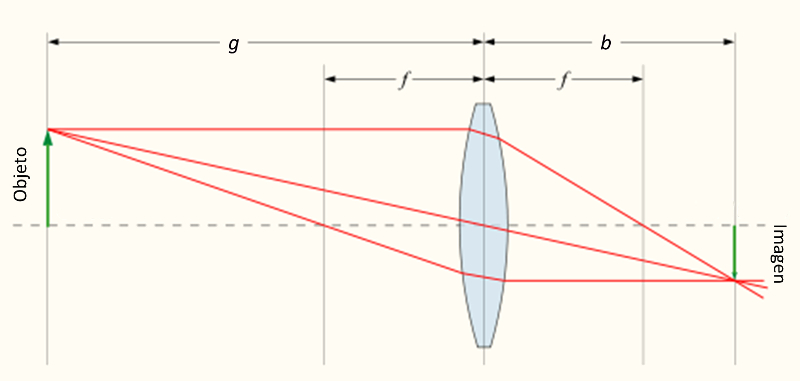
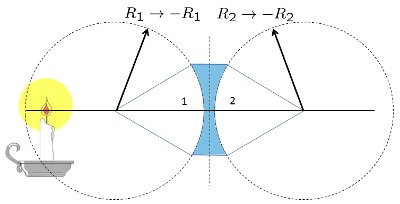
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:
ID:(9465, 0)
Position und Fokus von einer Konvexen Linse
Gleichung
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
 $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relación de similitud de los triángulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
ID:(3347, 0)
Proportionen der Größe und Position von einer konkaven Linse
Gleichung
Für jedes Objektiv können Sie charakteristische Strahlen zeichnen, mit denen Sie auf ähnliche Weise zeigen können, dass die Größen des Objekts und des Bildes im gleichen Verhältnis stehen wie ihre Abstände zum optischen Element (Objektiv oder Spiegel).
Wenn das Objekt eine Größe
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
ID:(3346, 0)
Gleichung der Fokus der Augen Linse
Gleichung
Si observamos la sección imagen (entre lente y cristalino) - cristalino - imagen sobre la retina, se puede aplicar la relación entre foco
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
En este caso no disponemos de la distancia entre imagen entre lente y cristalino y cristalino. Sin embargo se se define la la distancia entre lente y cristalino como
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
donde
ID:(3354, 0)
Entfernung Optical Lens Lens Gleichung
Gleichung
De la ecuación para el foco del lente óptico
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
y la del cristalino
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
la distancia entre lente y cristalino
| $\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$ |
Como es
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
\\n\\nse tiene que\\n\\n
$ s_i = \displaystyle\frac{1}{\displaystyle\frac{1}{ f_l } - \displaystyle\frac{1}{ s_o }}$
con lo que
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
se obtiene
| $\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$ |
donde
ID:(3355, 0)
Gleichung der Fokus für optische Linsen
Gleichung
Si observamos la sección objeto - lente óptico - imagen (entre lente y cristalino) se puede aplicar la relación entre foco
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Si en este caso el foco es
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
donde
ID:(3353, 0)
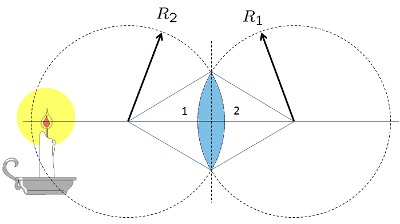
Berechnung des Fokus einer Einfache Bikonvexlinse
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
ID:(3432, 0)
Berechnung des Fokus eines bikonvexe dicken Linse
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracción
| $\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
ID:(3348, 0)
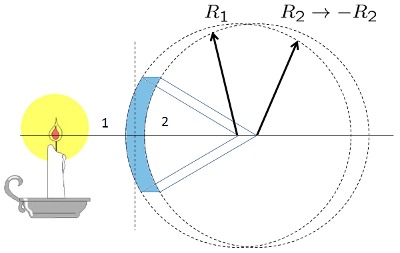
Cálculo del foco de un lente convexo-concavo grueso simétrico
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
ID:(3430, 0)
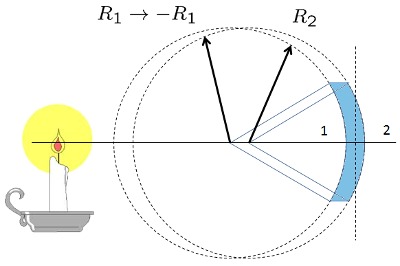
Cálculo del foco de un lente convexo-cóncavo grueso
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
| $\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$ |
ID:(3350, 0)
Berechnung des Fokus einer einfachen Bikonkaven Linse
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
ID:(3431, 0)
Cálculo del foco de un lente concavo-convexo grueso simétrico
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
ID:(3429, 0)
Die Berechnung des Fokus einer bi-konkave dicken Linse
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
| $\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
ID:(3349, 0)