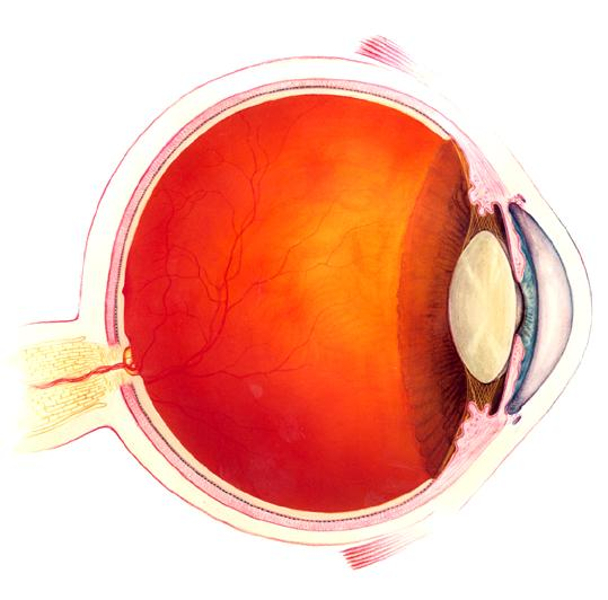
Eye
Description 
The eye is constituted by three key elements to be able to take advantage of the light:
- the lens adjusting light, about it more in the section on lenses
- the system that registers light and the nervous system that carries information to the brain
- the brain that processes the information received
In this section we will dedicate ourselves to the last point, since it is the point that defines what our eye captures.
ID:(218, 0)
See
Description 
There are two key aspects in the way we see.
On the one hand is the mechanism as we segment what we see in multiple sub-fields that we analyze individually. This analysis then focuses on recognizing known patterns.
Secondly, there is our ability to recognize the objects in each of these subfields. This requires being able to recognize an object and its spatial position.
ID:(488, 0)
Eye Lenses
Description 
Our eye is able to adjust the focal length of the lens and thereby focus on objects in a very wide range of distances.
In case the lens is not able to adapt the focus in said range, optical lenses can be used that modify the range that is able to focus it.
ID:(490, 0)
Position and focus of concave lens
Equation 
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relación de similitud de los triángulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
ID:(3347, 0)
Proportions size and position of concave lens
Equation 
For any lens you can draw characteristic beams with which you can similarly show that the sizes of the object and the image are in the same proportion as their distances to the optical element (lens or mirror).
If the object has a size
ID:(3346, 0)