User:
Molecular Heat Transport
Storyboard 
Faced with a temperature difference, heat flow processes are generated that lead to the passing of energy from areas of higher temperature to those of lower temperature, which ultimately leads to a homogeneous temperature.
ID:(1605, 0)
Difusión de calor
Image
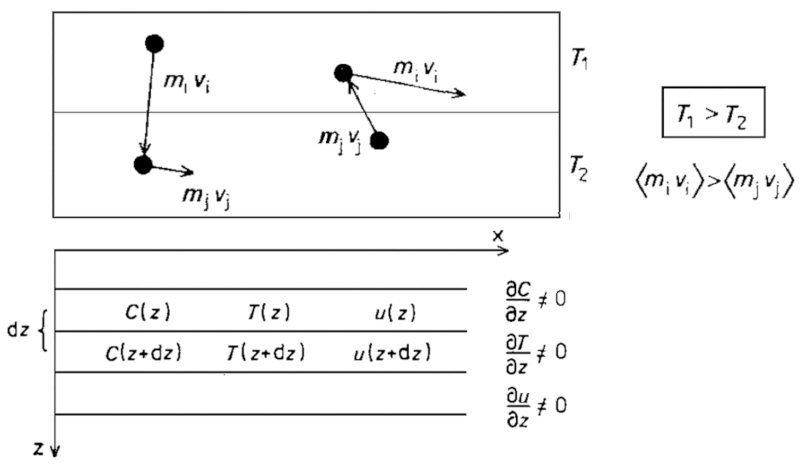
Uno de los procesos de difusión que ocurren en el océano es el de las energía que se expresa como el calor contenido en el agua. Físicamente corresponde a la difusión de partículas que tienen diferencia de temperatura.
ID:(12150, 0)
Temperature diffusion constant
Equation
The temperature in a system like water tends to diffuse until it is uniform throughout the volume. This diffusion is proportional to the ocean thermal conduction ($\lambda_T$) and inversely proportional to the sea water density ($\rho$) and the specific heat ($c$), which are necessary to increase the temperature.
Therefore, we introduce the thermal diffusion constant ($D_T$) as:
 $ D_T \equiv \displaystyle\frac{ \lambda_T }{ \rho c }$ |
The units are:
$\displaystyle\frac{\lambda_T}{\rho,c} \rightarrow \displaystyle\frac{J/m,s,K}{kg/m^3,J/kg K} = \displaystyle\frac{m^2}{s}$
which corresponds to a diffusion constant. The value for water is on the order of $10^{-6} , m^2/s$.
ID:(12048, 0)
Flujo de calor
Equation
El flujo de iones de sal se modela como un proceso de difusión en que el flujo es con que
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
\\n\\nEn este caso corresponde la variación de la concentración a variaciones en la densidad de la energía lo que se puede asociar vía la densidad y el calor especifico a la temperatura. Por ello\\n\\n
$dc \rightarrow \rho c dT$
La constante de difusión esta en este caso representada por la conductividad térmica por lo que la ecuación de la primera ley de Fick queda con como
| $ q_q = \lambda \displaystyle\frac{\partial T }{\partial z }$ |
ID:(12136, 0)
Flujo medio del calor
Equation
Si el flujo de calor instantáneo es densidad de Flujo calorico $W/m^2$, ocean thermal conduction $J/m s K$, posición $m$ and temperatura $K$ que
| $ q_q = \lambda \displaystyle\frac{\partial T }{\partial z }$ |
en el caso medio se puede expresar con variaciones finitas de modo de que con densidad de Flujo calorico $W/m^2$, ocean thermal conduction $J/m s K$, posición $m$ and temperatura $K$ es
| $ q_q = \lambda_T \displaystyle\frac{ \Delta T }{ \Delta z }$ |
ID:(12155, 0)
Valores de la conductividad térmica del agua marina
Image
La conductividad térmica es una función de la temperatura del agua marina. Esta aumenta en forma importante con el aumento de la temperatura.
ID:(12160, 0)
Variación temporal de la temperatura
Equation
Lo que corresponde a la variación de la concentración que
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
\\n\\ncorresponde ahora a la variación de la temperatura que es la densidad multiplicado por la densidad y la variación de la velocidad\\n\\n
$dc \rightarrow \rho c dT$
por lo que se puede describir la dinámica con mediante
| $ \rho c \displaystyle\frac{\partial T }{\partial t }=\displaystyle\frac{\partial q_q }{\partial x_i }$ |
ID:(13560, 0)
Variación temporal media de la temperatura
Equation
Si la variación temporal de la temperatura instantánea es que
| $ \rho c \displaystyle\frac{\partial T }{\partial t }=\displaystyle\frac{\partial q_q }{\partial x_i }$ |
en el caso medio se puede expresar con variaciones finitas de modo de que con es
| $ \rho c \displaystyle\frac{\Delta T }{\Delta t } = \displaystyle\frac{\Delta q_q }{\Delta z }$ |
ID:(12157, 0)
Ley de Fick para conductividad térmica constante
Equation
Como la primera ley de Fick en este caso es con densidad de Flujo calorico $W/m^2$, ocean thermal conduction $J/m s K$, posición $m$ and temperatura $K$
| $ q_q = \lambda \displaystyle\frac{\partial T }{\partial z }$ |
y la segunda ley de Fick en este caso es con igual a
| $ \rho c \displaystyle\frac{\partial T }{\partial t }=\displaystyle\frac{\partial q_q }{\partial x_i }$ |
se tiene la ley general de Fick para el caso de que la conductividad térmica no varíe con la posición que con es igual a
| $ \displaystyle\frac{\partial T }{\partial t } = - \displaystyle\frac{ \lambda }{ \rho c } \displaystyle\frac{\partial^2 T }{\partial x^2 }$ |
ID:(12158, 0)
Distribución de la temperatura en el tiempo
Equation
Para el caso de la conductividad térmica constante la ley general de Fick con
| $ c_{zt} =\displaystyle\frac{1}{\sqrt{4\pi D_N t }} e^{- z ^2/4 D_N t }$ |
se logra resolver esta ecuación obtenerse con la expresión
| $ T_{zt} =\displaystyle\frac{1}{\sqrt{4 \pi \lambda_T t / \rho c }} e^{- \rho c z ^2 /4 \lambda_T t }$ |
ID:(12159, 0)
0
Video
Video: Transporte Molecular de Calor